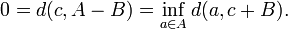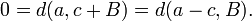Théorème de projection sur un convexe fermé - Définition
La liste des auteurs de cet article est disponible ici.
Autres applications
Ce théorème possède de multiples autres applications.
Il est utilisé en analyse fonctionnelle. Il peut donner lieu à des algorithmes programmables en dimension finie. Un exemple est donné par le théorème de Stampacchia.
En théorie des jeux, John von Neumann établit un théorème fondamental montrant l'existence de stratégies optimales pour les différents joueurs dans un contexte très général. Ce résultat est une conséquence du théorème de projection dans le cadre d'un Hilbert. Il possède de nombreuses conséquences, dont l'une célèbre est l'existence d'un Optimum de Pareto sous des hypothèses pas trop contraignantes en sciences économiques.
En programmation linéaire, ce théorème est utilisé pour, par exemple dans le cas des théorèmes de l'alternative trouver des solutions à des systèmes d'inéquations linéaires.
Principaux corollaires
Dans ce paragraphe E désigne un espace de Hilbert réel.
Supplémentaire orthogonal
Le théorème de projection est l'un des outils possibles pour prouver l'existence d'un supplémentaire orthogonal pour tout sous-espace vectoriel fermé d'un Hilbert (ou plus généralement, pour tout sous-espace vectoriel complet d'un préhilbert), donc l'existence d'une projection orthogonale sur ce sous-espace. (Une autre approche pour prouver ce corollaire est d'utiliser simplement l'inégalité de Bessel.)
Ce corollaire est le principal ingrédient de preuve du théorème de représentation de Riesz. Joint à ce dernier, il permet de démontrer le théorème de Lax-Milgram, qui aide à la résolution d'équation aux dérivées partielles.
Ce corollaire permet également, dans le cadre particulier hilbertien, de démontrer une version simplifiée du théorème de Hahn Banach sans faire appel au lemme de Zorn.
Séparation des convexes
Il existe une autre forme du théorème de Hahn-Banach :
Premier théorème de séparation — Soient A et B deux parties de E non vides et disjointes telles que A - B soit un convexe fermé. Il existe alors une forme linéaire continue f telle que :
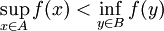
Ce résultat s'exprime encore sous la forme suivante :
Deuxième théorème de séparation — Soient A et B deux parties de E non vides et disjointes telles que A soit un convexe fermé et B un convexe compact. Alors il existe une forme linéaire continue f telle que :
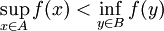
Dans le cas de la dimension finie, une forme du théorème de la séparation ne nécessite plus le caractère fermé du convexe :
Séparation en dimension finie — Si E est de dimension finie, soient x un élément de E et C un convexe ne contenant pas x, alors il existe une forme linéaire f non nulle telle que :
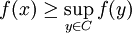
Pour démontrer les théorèmes de séparation, montrons tout d'abord un résultat préliminaire (qui est, dans les deux théorèmes, le cas particulier où B est un singleton) :
-
- Soient C un convexe fermé non vide de E et x un élément de E hors de C. Alors il existe une forme linéaire continue f telle que
 .
.Soient t la projection sur C et f la forme linéaire définie par :
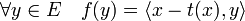
La deuxième caractérisation du projecteur montre que :
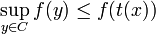
D'autre part, les vecteurs x et t(x) ne sont pas confondus car x n'est pas élément de C, par conséquent le carré de la norme de leur différence est strictement positif, d'où :
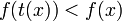
ce qui démontre le résultat préliminaire.
-
- Soient A et B deux parties de E non vides et disjointes telles que A - B soit un convexe fermé. Il existe alors une forme linéaire continue f telle que :
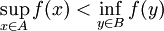
L'ensemble A - B est un convexe fermé non vide ne contenant pas le vecteur nul. Le résultat précédent montre l'existence d'une forme f telle que :
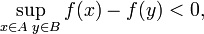
ce qui démontre la proposition.
-
- Le resultat précédent reste vrai si A est un convexe fermé et B un convexe compact.
Montrons que A - B est fermé. Soit c un élément de l'adhérence de cet ensemble, alors
Par compacité de A et continuité de l'application qui à tout a associe d(a,c+B), il existe donc un élément a de A tel que
Comme B est fermé, il contient alors a-c, donc c appartient à A-B. Ceci démontre que A - B est fermé. Les hypothèses de la proposition précédente sont rassemblées car A - B est convexe, elles permettent de conclure.
-
- Si E est de dimension finie, soient x un élément de E et C un convexe ne contenant pas x, alors il existe une forme linéaire non nulle telle que :
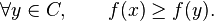
Pour tout élément y de C, notons Ty l'ensemble des formes linéaires f de norme 1 telles que f(x)-f(y) soit positif ou nul. L'objectif est donc de montrer que l'intersection de tous ces Ty est non vide. Or la sphère unité des formes linéaires est compacte car la dimension est finie, et chaque Ty est un fermé de ce compact (comme image réciproque d'un fermé par une application continue). D'après la propriété de Borel-Lebesgue, pour montrer que l'intersection des Ty est non vide, il suffit donc de montrer que pour toute partie finie non vide D de C, l'intersection des Ty quand y varie dans D est non vide.
Soit K l'enveloppe convexe d'une telle partie finie D. Elle forme un convexe fermé non vide et ne contient pas x. Le résultat préliminaire montre l'existence d'une forme linéaire f telle que f(x)>f(y) pour tout y dans K, en particulier pout tout y dans D, ce qui termine la démonstration.