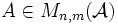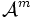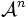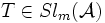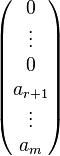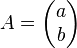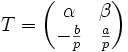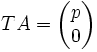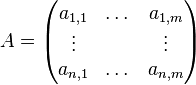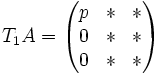Théorème des facteurs invariants - Définition

Échelonnement des matrices à coefficients dans un anneau euclidien

Quelle obstruction rencontre-t-on dans le cas d'une matrice à coefficients dans un anneau euclidien? La principale est que la non nullité d'un coefficient n'assure pas qu'on puisse s'en servir comme pivot pour des opérations de transvection : dans l'exemple précédent, on s'est servi de 2 comme pivot, et on a été amenés à faire des calculs avec son inverse ; ce faisant, on est sorti du cadre initial d'une matrice à coefficients entiers.

Échelonnement des matrices lignes et colonnes

Il existe un palliatif. Regardons pour une matrice de taille à coefficients dans un anneau euclidien :

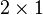
Dans le cas où a et b sont non nuls, soit p un plus grand diviseur commun de a et b. On considère alors la matrice :

avec la relation . Le fait de se placer dans un anneau principal assure l'existence des coefficients α et β (voir théorème de Bachet-Bézout), et le fait de se placer dans un anneau euclidien donne l'algorithme d'Euclide pour les calculer. On constate l'égalité :

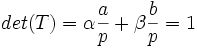
on s'est ainsi ramené à une matrice colonne avec un coefficient nul, par une opération sur les lignes de la matrice A ; on peut voir cette opération comme une généralisation de la transvection. Remarquons que la matrice de transvection généralisée T est inversible puisque de déterminant (égal à 1) inversible dans l'anneau considéré. Dans la cas où b est nul, on prend T = Id, dans le cas où a est nul, on prend . On voit en particulier que les matrices de transvection généralisées qu'on considère ne comprennent pas les matrices de permutation qui apparaissaient dans la décomposition LU ; c'est dû au choix restrictif de se limiter à des matrices de déterminant 1 ; leur absence est toutefois facilement palliée, comme on l'a vu ci-dessus.

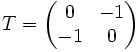
Pour traiter le cas d'une matrice colonne de taille quelconque, il suffit d'effectuer d'abord une opération entre la première et la deuxième ligne, pour annuler le deuxième coefficient, puis entre la première et la troisième pour annuler le troisième, etc. Ainsi, pour , il existe T produit de matrices de transvection généralisées telle que , où p est le pgcd des coefficients a_i.

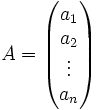
Le cas d'une matrice ligne s'en déduit par transposition.

Matrices de transvection généralisées, et opérations élémentaires

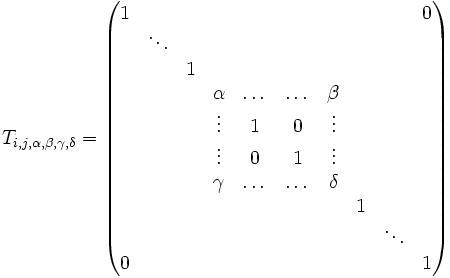
On s'intéresse maintenant à des matrices de taille , éventuellement rectangulaires, toujours à coefficients dans un anneau euclidien. Les matrices de transvection généralisées codant les opérations sur les lignes seront donc des matrices carrées de taille n, et celles codant les opérations sur les colonnes des matrices carrées de taille m. Pour faire une opération entre les rangées i et j, il faut donc considérer les matrices :

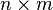
avec αδ − βγ = 1, où les coefficients α,β apparaissent sur la ligne i, et γ,δ sur la ligne j. On remarque la relation suivante : .

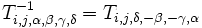
Multiplier une matrice A, dont les lignes sont L_i, à gauche par une telle matrice, c'est remplacer la ième ligne L_i de A par αL_i + βL_j, et la jème ligne par γL_i + δL_j. Pour obtenir une opération sur les colonnes, il faut effectuer une multiplication à droite par une matrice de transvection généralisée.

Dans le cas où α = δ = 1, et où un des deux coefficients β ou γ est nul, on retrouve une matrice de transvection proprement dite ; dans le cas où α = δ = 0, et β = − γ = + − 1, on trouve une matrice qui va jouer le rôle de matrice de transposition ; convenons d'appeler anti-transposition l'opération correspondante.

Algorithme d'échelonnement pour les matrices de taille quelconque

Commençons à décrire l'algorithme. Pour une matrice :

on commence par multiplier à gauche par des matrices de type T_1,j, pour j allant de 2 à n ; on effectue ces opérations en considérant seulement leur effet sur le premier vecteur colonne de la matrice A. D'après ce qu'on a vu pour les opérations sur les lignes d'un vecteur colonne, on parvient ainsi à annuler tous les coefficients sous-diagonaux de la première colonne de A, et le premier coefficient de la nouvelle matrice est précisément un pgcd des coefficients de la première colonne de A :

On veut ensuite multiplier par des matrices de type T_2,j, pour j > 2, pour annuler tous les coefficients sous-diagonaux de la deuxième colonne ; de telles opérations ne font pas intervenir la première ligne ; tous les coefficients de la première colonne, autre que celui en position (1,1), qui seront ainsi obtenus seront donc combinaison linéaire des coefficients nuls de la première colonne : ils seront nuls. Il faut ensuite multiplier par des matrices de type T_3,j, pour annuler les coefficients sous-diagonaux de la troisième colonne, etc.

On obtient en définitive une égalité avec une matrice de la forme : où les coefficients p_i sont non nuls. La matrice obtenue est dite sous forme échelonnée en lignes, voir matrice échelonnée.

L'échelonnement en colonnes s'en déduit par transposition.

Théorème d'échelonnement

Soit un anneau principal, et A une matrice de . Alors, il existe une matrice (c'est-à-dire inversible et de déterminant 1), produit de matrices de transvection généralisées, telle que la matrice soit sous forme échelonnée en lignes. Si, de plus, l'anneau est euclidien, on dispose d'un algorithme pour calculer la matrice T, dont la complexité est polynômiale en la taille de la matrice A et la taille de ses coefficients.

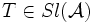
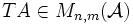
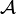
Conséquences

L'algorithme d'échelonnement est suffisant pour bon nombre de calculs : le rang de la matrice A est égal au nombre de lignes non nulles de sa forme échelonnée ; le déterminant, dans le cas d'une matrice carrée de rang maximal, sera le produit des coefficients p_i de la matrice échelonnée.

On peut aussi en déduire des équations et paramétrisations des noyaux et images des matrices, vues comme applications linéaires ; par exemple, pour , vue comme application linéaire de dans , et telle que AT soit échelonnée en colonnes, les éléments du noyau de AT sont de la forme , où les r premières lignes sont nulles, pour r le rang de A, et donc le nombre de colonnes non nulles de AT ; et donc les éléments du noyau de A sont engendrés par les m − r derniers vecteurs colonnes de T ^{− 1}.