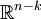Théorie de Morse - Définition
La liste des auteurs de cet article est disponible ici.
Théorème du h-cobordisme
Deux variétés différentielles compactes sans bord M et N de même dimension n sont dites en cobordisme lorsqu'il existe une variété différentielle compacte X, de bord la somme disjointe de M et de N. La variété X est dite réaliser un cobordisme entre M et N. L'existence d'un tel cobordisme ne dépend que de la classe d'isomorphisme de M et de N. De fait, le cobordisme peut être regardé comme une relation d'équivalence sur l'ensemble des variétés différentielles de dimension n à difféomorphisme près.
Le théorème du h-cobordisme permet de construire par récurrence et à difféomorphisme près toutes les variétés en cobordisme avec une variété différentielle compacte M donnée.
Théorème du h-cobordisme :
Formalisation de la théorie
La théorie de Morse s'applique à une fonction différentiable réelle f sur une variété différentielle M. Les points critiques de f sont les points où la différentielle de f s'annule, les valeurs critiques sont les valeurs prises par f en ces points. En chacun des points, il est possible de définir le hessien de f comme une forme quadratique sur TxM. Le point critique x est dit non dégénéré lorsque le hessien correspondant est une forme quadratique non dégénérée. L'indice de x est défini comme la dimension du plus grand sous-espace défini négatif.
Les lignes de gradient
Les lignes de gradient sont un outil adapté à la comparaison des sous-niveaux entre eux. Dans le cas de la "fonction hauteur" donnée en exemple, il s'agirait des lignes de plus grande pente tracées sur le tore. Pour les définir en général, il faut munir la variété d'une métrique riemannienne. Il est alors possible d'introduire le champ de vecteurs gradient
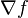
-
![\dot{x}(t)=\nabla f\left[x(t)\right]](https://static.techno-science.net/illustration/Definitions/autres/3/323ceaf64997819949facc34bc4b02ed_29123089d9ca79e320aa9daa5257f141.png)
Les lignes de gradient sont orthogonales aux hypersurfaces de niveau, définies par l'équation f=constante. Sur une variété riemannienne compacte sans bord (M, g), le champ de gradient est globalement intégrable, c'est-à-dire que toutes les lignes de gradient sont définies sur tout R.
Évolution des sous-niveaux
Les sous niveaux Mz de la fonction f sont définie comme précédemment. Les deux théorèmes suivants permettent de comparer les sous-niveaux entre eux.
Théorème : description des zones sans point critique
Si a<b, et si f − 1([a,b]) est compact sans point critique, alors Ma et Mb sont des variétés à bord difféomorphes.
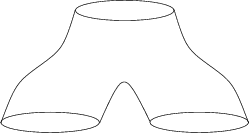
Plus précisément, la partie ajoutée à Ma pour obtenir Mb, qui ressemble à une jambe de pantalon, peut être décrite en suivant les lignes de gradient de la fonction f. Cette partie est difféomorphe au produit
![[a,b]\times f^{-1}(\{a\})](https://static.techno-science.net/illustration/Definitions/autres/f/f90d0addb790750f0e9da7b8e1f24523_c0f6c3e6745c7db748c7ac7f09a59889.png)
Théorème : passage d'un point critique
Soit p un point critique non dégénéré de f d'indice d' et q=f(p) la valeur critique correspondante. On suppose que a
Fonctions de Morse
Une fonction de Morse f est une fonction de classe C2 dont tous les points critiques sont non dégénérés. Selon un résultat de René Thom, si la variété M est compacte sans bord, les fonctions de Morse constituent un ouvert dense de l'espace de Fréchet Ck(M,R) des fonctions de classe Ck sur M, et ce pour toute classe de régularité
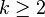
Sur une variété riemannienne compacte sans bord (M, g),les lignes de gradient admettent des limites en
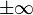
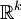
La variété instable en a est définie de même comme réunion des lignes de gradient originaires de a. Toujours pour un point d'indice k, elle est difféomorphe à