Théorie des équations (mathématiques) - Définition

Introduction

La théorie des équations est la partie des mathématiques s'occupant des problèmes posés par les équations polynomiales de tous les degrés. Se trouvent ainsi rassemblés les problèmes de résolution de ces équations, d'estimation des solutions, de détermination du signe de ces solutions, des algorithmes de résolution et tous les problèmes connexes.

L'expression « théorie des équations » a été très utilisée au XIX^e siècle et dans la première moitié du XX^e siècle. Depuis lors, bien que le champ mathématique soit toujours actif, l'expression est de moins en moins utilisée hormis en histoire des sciences. Cependant il n'y en a aucune autre de proposée pour cette partie des mathématiques.

Prologue

Dans toute la suite, sauf mention spéciale, on considère un polynôme d'une seule variable à coefficients réels ou complexes dont on cherche les racines réelles ou complexes.

En pratique on est souvent amené à résoudre une équation polynômiale à coefficients réels ou complexes.

Or seules les équations polynômiales générales de degrés inférieurs ou égaux à quatre sont résolubles par radicaux. Pour les équations de degrés supérieurs, sauf dans quelques cas particuliers et en excluant la solution générale d'Hermite pour le degré cinq qui fait intervenir des fonctions elliptiques, il ne reste que le calcul numérique.

La majorité des algorithmes connus pour calculer une solution repose sur une amorce proche de la solution cherchée. Se pose donc la question de déterminer une région où se trouvent les solutions.

Souvent, on n'a pas besoin de connaître les solutions avec précision. Une estimation de ces solutions suffit, voire seulement le nombre ou le signe de ces solutions, quand ce n'est pas un simple majorant.

L'objet de cet article est de donner un panorama des méthodes ingénieuses d'estimation de ces solutions découvertes depuis parfois longtemps.

Il ne sera pas donné, en général, de démonstration de ces résultats. On se reportera soit à la bibliographie soit aux articles originaux pour les démonstrations.

On consultera avec profit l'article théorie des équations (histoire) qui traite de l'histoire de la résolution par radicaux.

Positions des problèmes

Le premier objet de la théorie est l'étude des rapports entre les coefficients et les racines d'un polynôme. On verra que les relations entre les coefficients et les racines sont de plus en plus compliquées à mesure que le degré du polynôme augmente. Élémentaire au premier degré, raisonnable au second, l'expression des racines en fonction des coefficients devient plus difficile avec les troisième et quatrième degré, très complexe au cinquième degré et inextricables au-delà.

Définitions et conventions

Dans la suite, les polynômes considérés sont donnés sous forme développée selon la formule .

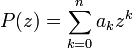
Le coefficient a_k est le coefficient de la puissance k-ieme de la variable z.

Le degré du polynôme P est égal à son coefficient non nul de rang le plus élevé.

Dans le cas où la variable considérée est réelle, on l'écrira x.

On appelle racine de P toute valeur α, réelle ou complexe, telle que P(α) = 0.

La conjecture de Girard et le théorème de D'Alembert-Gauss

C'est au XVII^e siècle qu'apparaît, sous la plume d'Albert Girard, la première formulation explicite de la conjecture

« Tout polynôme de degré n à coefficients complexes admet n racines complexes. »

Il n'essaie d'ailleurs pas de la démontrer. Il faut attendre D'Alembert, en 1746, pour une première tentative qui ne convainquit pas. Les tentatives d'Euler (1749), de Faunsenet (1751), Lagrange (1771) et Gauss (1799) ne sont guère plus convaincantes. Elles butent essentiellement sur des questions qui ne peuvent avoir de réponse par des méthodes de cette époque. Il faut attendre la démonstration de Gauss de 1815 pour que la conjecture soit enfin démontrée. On peut la démontrer par différentes méthodes mais la plus courante est celle qui résulte du théorème de Liouville.

Théorème de Liouville:

« Toute fonction holomorphe et bornée dans le plan complexe est constante.  »

et qu'on peut démontrer par les inégalités de Cauchy.

La démonstration de la conjecture de Girard consiste à montrer que tout polynôme de degré n admet au moins une racine complexe. Et, par factorisation, il en admet donc exactement n. Soit donc P un polynôme de degré n à coefficients complexes. Supposons que P n'ait pas de racine. Alors 1/P est une fonction holomorphe dans tout le plan complexe et bornée. Donc, d'après le théorème de Liouville, 1/P est constante et P aussi. Donc tout polynôme non constant admet un zéro. D'où le théorème.

Corollaire: Tout polynôme de degré n à coefficients complexes se décompose en un produit de n termes du premier degré faisant apparaître les racines complexes α_k.

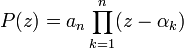
Tout polynôme de degré n à coefficients réels peut s'écrire comme le produit de termes de degré au plus deux à coefficients réels. Les termes du second degré sont des polynômes n'ayant pas de racine réelle.

Dans un anneau quelconque, on n'a pas le théorème de D'Alembert-Gauss

On a tendance à exprimer le théorème de D'Alembert-Gauss sous la forme: "tout polynôme de degré n admet n racines" ou bien sous la forme "tout polynôme de degré n admet au plus n racines" suivant l'ensemble dans lequel on recherche les racines. Les deux énoncés sont faux sans autre précision. Un polynôme de degré n peut fort bien avoir plus de n racines si l'on recherche les racines dans un anneau quelconque. Par exemple le polynôme (x-2)(x-3), qui est de degré 2, admet quatre racines dans Z/6Z: 0, 2, 3, et 5=-1.