Tourbillon (physique) - Définition

Source: Wikipédia sous licence CC-BY-SA 3.0.
La liste des auteurs de cet article est disponible ici.

- Introduction - Terminologie - Météorologie et Océanographie - Dynamique des fluides - Bibliographie - Autres utilisations

Dynamique des fluides

En dynamique des fluides, le tourbillon est le rotationnel de la vitesse du fluide. On peut également le considérer comme la circulation par unité de surface en un point dans un flux :

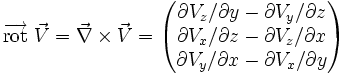
{\overrightarrow{\mathrm{rot}}}\ \vec V = \vec \nabla \times \vec V = \begin{pmatrix} {\partial V_z / \partial y} - {\partial V_y / \partial z} \\ {\partial V_x / \partial z} - {\partial V_z / \partial x}\\ {\partial V_y / \partial x} - {\partial V_x / \partial y} \end{pmatrix}

où $\vec V$ est le vecteur tri-dimensionnel de vitesse selon les coordonnées x, y et z et $\vec\nabla$ l'opérateur nabla.

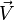
C'est une quantité vectorielle dont la direction est le long de l'axe de rotation du fluide. Ainsi, pour un flux à deux dimensions quelconque (a et b), le vecteur de tourbillon se retrouve dans l'axe perpendiculaire au plan de rotation (c) et l'équation se réduit à :

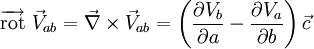
On retrouve différents théorèmes reliés au tourbillon en physique.

Bibliographie

(en) Batchelor, G. K., (1967, reprinted 2000) An Introduction to Fluid Dynamics, Cambridge Univ. Press
(en) Ohkitani, K., "Elementary Account Of Vorticity And Related Equations". Cambridge University Press. January 30, 2005. ISBN 0521819849
(en) Chorin, Alexandre J., "Vorticity and Turbulence". Applied Mathematical Sciences, Vol 103, Springer-Verlag. March 1, 1994. ISBN 0387941975
(en) Majda, Andrew J., Andrea L. Bertozzi, and D. G. Crighton, "Vorticity and Incompressible Flow". Cambridge University Press; 1st edition. December 15, 2001. ISBN 0521639484
(en) Tritton, D. J., "Physical Fluid Dynamics". Van Nostrand Reinhold, New York. 1977. ISBN 0198544936
(en) Arfken, G., "Mathematical Methods for Physicists", 3rd ed. Academic Press, Orlando, FL. 1985. ISBN 0120598205

v · d · m Données et variables météorologiques
Données de mesure	Albédo · Foudre · Isotherme zéro degré (Niveau de congélation) · Nébulosité · Point de rosée · Point de givrage · Précipitation · Pression atmosphérique · Réflectivité radar (en dBZ) · Température · Température de surface de la mer · Température du thermomètre mouillé · Vent · Visibilité (Profondeur optique)
Variables	EIC · EPCD · Fréquence de Brunt-Väisälä · Gradient thermique adiabatique · Hélicité · Humidité relative · Humidité absolue · Humidité absolue de saturation · Instabilité latente · Instabilité potentielle · Longueur de Monin-Obukhov · Niveau de condensation par ascension · Niveau de convection libre · Rapport de mélange · Refroidissement éolien · Température équivalente · Température potentielle · Température pseudo-potentielle du thermomètre mouillé · Theta-e · Température virtuelle · Tourbillon
Concepts	Convection · Hygrométrie · Évapotranspiration
Indices	Indice WBGT · Indice humidex · Indice d'aridité · Refroidissement éolien · Indice forêt météo · Indice de rayonnement UV · Indice de soulèvement · Indice de stabilité de Showalter
Diagrammes	Diagramme climatique · Diagramme de Stüve · Émagramme · Hodographe · Skew-T ou Émagramme à 45 degrés · Téphigramme
Glossaire de la météorologie

Autres utilisations

La notion de tourbillon est importante dans bien d'autres domaines de la dynamique des fluides. Par exemple, on peut estimer la distribution de la portance sur une aile d'avion d'envergure finie en supposant qu'à chaque section de l'aile est associé un tourbillon semi-infini vers l'aval. Il est alors possible de déterminer l'intensité de ces tourbillons en utilisant le critère selon lequel il n'y a pas de flux induit à travers la surface de l'aile. On additionne ensuite les intensités de tous les tourbillons pour trouver une valeur approchée de la circulation autour de l'aile. La portance est alors le produit de la circulation, de la vitesse de l'air et de sa masse volumique.