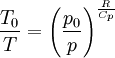Gradient thermique adiabatique - Définition

Introduction

Le gradient thermique adiabatique est, dans l'atmosphère terrestre, la variation de température de l'air avec l'altitude (autrement dit le gradient de la température de l'air), qui ne dépend que de la pression atmosphérique, c'est-à-dire :

• sans considération d'échange de chaleur avec l'environnement (autres masses d'air, relief) ;
• sans considération de condensation (formation de nuages) ni de précipitation.

Ce concept a une grande importance en météorologie, ainsi qu'en navigation aérienne et maritime.

Mécanisme

La variation de pression de l'atmosphère est très complexe. Toutefois, pour comprendre un certain nombre de mécanismes météorologiques, on peut s'en tenir à un modèle très simple qui ne dépend que de l'altitude.

Dans la troposphère, on peut considérer l'air comme un gaz parfait : la pression est relativement faible (de l'ordre de 10⁵ pascals) et les molécules n'ont pas d'interaction autre que des chocs entre elles. Ainsi, si une masse d'air n'échange pas de chaleur avec son environnement (conditions dites adiabatiques), sa température ne dépend que de sa pression : lorsque l'air se comprime, il s'échauffe, et lorsqu'il se détend, il refroidit.

Dans une atmosphère totalement sèche, on a  :

C·dT + M·g·dz = 0 ;

où

• C est la capacité calorifique molaire à pression constante de l'air ;
• dT est la variation élémentaire de température pour une variation d'altitude dz ;
• M est la masse molaire de l'air ;
• g est l'accélération de la gravité.

Ce résultat s'obtient en posant que l'enthalpie généralisée est constante. '

Ainsi, si une masse d'air s'élève, elle se refroidit par détente adiabatique (puisque la pression de l'air diminue), et si elle descend, elle se réchauffe par compression adiabatique (puisque la pression de l'air augmente). Cette variation de température avec l'altitude permet de définir le gradient thermique adiabatique.

Gradient adiabatique sec

Identification des courbes adiabatiques sèches sur un diagramme thermodynamique appelé émagramme qui relie la variation de température et la pression dans l'atmosphère

Dans la troposphère, la température d'une parcelle s'élevant selon le gradient thermique adiabatique est:

avec

• T : température au niveau de référence ;
• p : pression au niveau de référence ;
• p : pression à l'altitude étudiée ;
• R : constante des gaz parfaits ;
• C : capacité thermique de l'air à pression constante

Il vaut −9,76 °C par km. On utilise souvent la valeur approchée de −10 °C par km, soit −1 °C pour 100 m.

Ce gradient est dit gradient adiabatique sec (car l'humidité ne joue aucun rôle). C'est celui-ci qu'on peut voir sur le diagramme thermodynamique qu'on appelle émagramme ci-joint (lignes pleines nommées dry adiabat) où on voit que la pente est toujours la même quelle que soit la température (les courbes sont parallèles).

Gradient adiabatique humide ou l'influence de l'humidité

Identification des courbes adiabatiques humides sur un émagramme

En soi, la présence de vapeur d'eau n'a pas d'influence sur le gradient adiabatique. Toutefois, en dessous d'une certaine température, la vapeur d'eau se condense. Cette température dépend de deux choses :

• la teneur en vapeur d'eau ;
• la présence de poussières permettant aux gouttelettes de se former (sorte de floculation).

En effet, hors présence de poussière, on a de la sur-vaporisation : l'eau reste sous forme de vapeur car les gouttelettes qui se forment ne sont pas stables (voir aussi l'article Surfusion).

Si la vapeur d'eau se condense, alors cette liquéfaction libère de la chaleur (chaleur latente de vaporisation) : le Soleil a chauffé l'eau de l'océan et du sol, et cette chaleur a été emmagasinée dans l'évaporation ; le changement d'état inverse redonne cette chaleur. Ainsi, si la vapeur d'eau se condense, la masse d'air se réchauffe.

De fait, la condensation réchauffant l'air, la valeur absolue du gradient est plus faible. Ce taux dépend du relâchement de chaleur latente qui lui dépend légèrement de la pression mais plus fortement de la température ambiante. Le taux adiabatique humide n'est donc pas une constante et varie selon les courbes « Moist Adiabat » que l'on voit sur l'image de l'émagramme. Ces courbes changent de pente avec la température et la pression, se rapprochant de l'adiabatique sèche à mesure que l'humidité de l'air est faible (température très froide et/ou faible pression).

Par exemple, le taux moyen est souvent mentionné comme −6 °C/km mais en fait varie ainsi :

• à 100 kPa de pression : de −3,15 °C/km (40 °C) à −9,78 °C/km (-40 °C)
• à 50 kPa de pression : de −2,55 °C/km (40 °C) à −9,54 °C/km (-40 °C).

On parle de « gradient adiabatique saturé » ou de « pseudo-adiabatique saturé » (pseudo car on élimine l'eau à mesure qu'elle se condense).