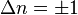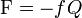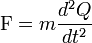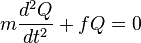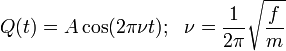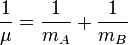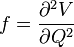Vibration moléculaire - Définition

En mécanique quantique

Dans l'approximation harmonique, l'énergie potentielle est une fonction quadratique des conditions normales. En résolvant l'équation de Schrödinger, les états énergétiques pour chaque coordonnée normale sont données par :

,

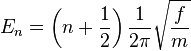
où n est un nombre quantique pouvant prendre comme valeurs 0, 1, 2 ... La différence dans l'énergie lorsque n varie de 1 est ainsi égale à l'énergie dérivée utilisée en mécanique classique. On pourra se reporter à l'article oscillateur harmonique quantique pour plus de précisions. Connaissant les fonctions d'ondes, certaines règles de sélection peuvent être formulées. Ainsi, pour un oscillateur harmonique, les transitions sont permises seulement quand le nombre quantique est modifié d'une unité,

mais cela ne s'applique pas à un oscillateur anharmonique ; l'observation des harmoniques est seulement possible car les vibrations sont anharmoniques. Une autre conséquence de l'anharmonicité est que les transitions comme entre les états n=2 et n=1 ont un tout petit peu moins d'énergie que les transitions entre l'état fondamental et le premier état excité. Une telle transition donne une croissance vers une bande chaude.

Intensités

Dans un spectre infrarouge, l'intensité d'une bande d'absorption est proportionnelle à la dérivée au moment dipôlaire moléculaire par rapport à la coordonnée normale. L'intensité des bandes Raman dépend de la polarisabilité.

En mécanique newtonienne

Les vibrations moléculaires peuvent être traitées en utilisant la mécanique classique afin de calculer les fréquences de vibrations correctes. Le postulat de base est que chaque vibration peut être traitée comme si elle correspondait à un ressort. Dans l'approximation harmonique, un ressort obéit à la loi de Hooke : la force requise pour étirer le ressort est proportionnelle à son extension. Le coefficient de proportionnalité est connue sous le nom de constante de force f. L'oscillateur anharmonique sera considéŕe par ailleurs.

Selon la deuxième loi du mouvement de Newton, cette force est égale au produit de la masse m par l'accélération a :

Par identité, on obtient l'équation suivante :

La solution à cette équation du mouvement harmonique simple est :

A est le maximum d'amplitude de la coordonnée de vibration Q. Il reste à définir la masse, m. Dans une molécule homonucléaire diatomique comme N₂, il s'agit de la masse des deux atomes. Dans le cas d'une molécule diatomique hétéronucléaire, AB, elle correspond à la masse réduite, μ définie par :

L'utilisation de la masse réduite permet d'assurer que le centre de masse de la molécule ne soit pas affecté par la vibration. Dans l'approximation harmonique, l'énergie potentielle de la molécule est une fonction quadratique de la coordonnée normale. Il s'ensuit que la constante de force est égale à la dérivée seconde de cette énergie potentielle.

Lorsque deux vibrations normales ou plus ont la même symétrie, une analyse des coordonnées normales complète doit être effectuée (voir méthode GF). Les fréquences de vibrations,ν_i, sont obtenues à partir des valeurs propres, λ_i, du produit matriciel GF. G est la matrice de nombres dérivés des masses des atomes et de la géométrie de la molécule et F est une matrice dérivée des constantes de forces. De plus amples informations sur la détermination de ces valeurs propres peuvent être obtenues en consultant l'ouvrage de P. Gans.