Voyage relativiste - Définition
La liste des auteurs de cet article est disponible ici.
Étude d'un cas concret
Une proposition est faite dans la sous-section citée sur l'énergie nucléaire d'utiliser d'une manière ou d'une autre l'énergie nucléaire dans le but d'obtenir ce genre de vitesse, en raccourcissant ainsi le temps de voyage d'un facteur 100 par rapport aux terriens.
Le but du présent article est de calculer les conséquences d'une telle entreprise, sur les bases mêmes de la relativité restreinte utilisée pour obtenir cet effet.
On n'entrera pas dans les détails de la technique à mettre en œuvre pour la réalisation, mais on se bornera à calculer l'énergie à utiliser dans le cas le plus favorable de rendement, et la perte de masse ainsi occasionnée. On supposera par la suite le lecteur familier avec les formules fondamentales de la relativité restreinte, sinon, on lui conseillera de sauter aux .
Hypothèses de base
On se limitera à un système dont le rendement de propulsion est
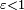
Si l'on considère le vaisseau de masse courante
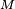
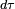
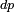
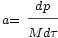
Il va également perdre une énergie
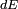
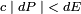
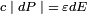
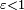

On a alors
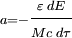
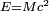
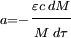
Pour passer aux formules globales, et non plus différentielles, nous devons tenir compte du fait que le système inertiel du vaisseau change tout le temps. Le plus commode est d'introduire le paramètre additif

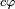
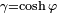
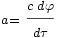
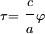
On arrive enfin à la relation :
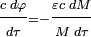
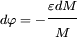
Cette équation s'intègre par
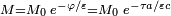
Application numérique
Le rapport moyen entre le temps terrestre


Le rapport instantané
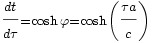

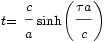
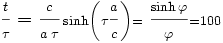
Par résolution numérique, on trouve
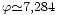
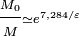
Pour la mission complète, accélération-décération, aller-retour, il faut diviser la masse initiale 4 fois de suite par ce facteur, soit par un facteur global irréaliste de 4,5·1012 pour un rendement irréaliste de ε=100%, et quelque 101265 pour ε=1% …
La distance parcourue en accélération


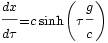
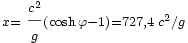
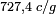
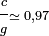
Donc, dans les conditions indiquées, on « pourrait » aller à environ 1400 années-lumière, mais il faudrait pour cela un temps propre de