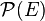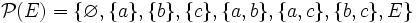Ensemble des parties d'un ensemble - Définition
En mathématiques, l'ensemble des parties d'un ensemble désigne l'ensemble des sous-ensembles de cet ensemble.
Définition
Soit E un ensemble. L'ensemble des parties de E est :
-
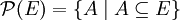
Il est noté
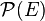
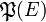
Dans la théorie axiomatique des ensembles, de Zermelo et celle de Zermelo-Fraenkel, l'existence, pour tout ensemble E, d'un tel ensemble pour tout ensemble E est postulée par l'axiome de l'ensemble des parties.
Propriétés
Cardinalité
Cardinalité finie
Soit E est un ensemble de cardinal fini, card(E) = n. Le cardinal de
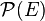
-
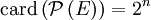
Cardinalité infinie
On a pour tout entier naturel n, n < 2n. Ce résultat se généralise en cardinalité infinie. Le théorème de Cantor énonce que l'ensemble des parties d'un ensemble (fini ou non) a une cardinalité strictement supérieure à celle de l'ensemble de départ : il existe une injection d'un ensemble dans l'ensemble de ses parties (par exemple on associe à un élément le singleton auquel il appartient), mais aucune bijection.
Tout ensemble de même cardinal que N, l'ensemble des entiers naturels, est dit dénombrable, et c'est le plus petit cardinal infini. Le théorème de Cantor montre en particulier que P(N) n'est pas dénombrable, ce qui peut s'interpréter en disant que l'on ne peut " numéroter " de façon exhaustive les sous-ensembles de N. C'est-à-dire que, dès que l'on a une suite de sous-ensembles de N indexée par les entiers, on trouve forcément un sous-ensemble de N qui n'apparaît pas dans cette suite.
Quelle peut-être la cardinalité d'un ensemble de parties de N, c'est-à-dire d'un sous-ensemble de P(N) ? Georg Cantor pensait qu'elle ne pouvait être que finie, dénombrable, ou celle de P(N). C'est l'hypothèse du continu qui n'est ni démontrable ni réfutable dans la théorie des ensemble ZFC.
Algèbre de Boole
L'ensemble des parties de l'ensemble E, muni des opérations d'union, d'intersection et de complémentation, forme un exemple typique d'algèbre de Boole. On peut montrer,en particulier que toute algèbre booléenne finie est isomorphe à l'algèbre booléenne de l'ensemble des parties d'un ensemble fini. Cela n'est pas vérifié pour les algèbres booléennes infinies, mais toute algèbre booléenne infinie est une sous-algèbre d'une algèbre booléenne de l'ensemble des parties d'un ensemble.
Comme pour toute algèbre de Boole, on peut définir une structure d'anneau, en introduisant une opération définie à partir de la réunion et de l'intersection : la différence symétrique. L'ensemble des parties de l'ensemble E muni de la différence symétrique est un groupe abélien. L'élément neutre est l'ensemble vide. Chaque sous-ensemble est son propre opposé. Ce même ensemble est un semigroupe commutatif lorsqu'il est muni de l'opération d'intersection. On peut donc montrer (en utilisant les lois de la distributivité) que l'ensemble des parties d'un ensemble, muni de la différence symétrique et de l'intersection, est un anneau commutatif dont tout élément est idempotent (x2=x, ici le produit est l'intersection), c’est-à-dire un anneau de Boole (réciproquement à tout anneau de Boole on peut associer une algèbre de Boole).
Exemples
Soit E = {a,b,c} un ensemble de trois éléments. Les sous-ensembles de E sont :
-
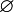
- {a}
- {b}
- {c}
- {a,b}
- {a,c}
- {b,c}
- E = {a,b,c}
L'ensemble des parties de E est donc :
Notation exponentielle
En théorie des ensembles, XY désigne l'ensemble des fonctions de Y dans X. Comme 2 peut être défini comme l'ensemble {0, 1} dans la construction des entiers naturels de von Neumann, 2E peut désigner l'ensemble des fonctions de E dans {0, 1}.
En associant une fonction de 2E avec l'ensemble antécédent de 1 par cette fonction, on établit une bijection immédiate entre 2E et
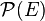
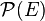
Il peut donc arriver que l'on identifie 2E et