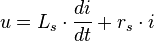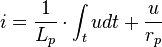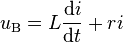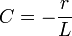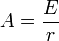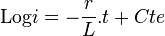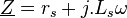Bobine (électricité) - Définition
En électricité, ce terme peut désigner deux dispositifs :
- Un dipôle électrique, parfois appelé inductance ou self
- Un dispositif destiné à produire des tensions élevées.
Le dipôle bobine
Une bobine est un terme générique en électricité pour désigner un dipôle formé de une à une multitude de spires de fil autour d'un noyau. Ce noyau peut être vide ou en un matériau favorisant l'induction magnétique (matériau ferromagnétique, afin d'augmenter la valeur de l'inductance). Il peut être également fermé, avec ou sans entrefer, afin de constituer un circuit magnétique fermé.
C'est donc un dipôle auto-inductif plus ou moins linéaire qui est caractérisé principalement par son inductance, mais également par une résistance électrique (celle du fil utilisé, a priori faible), mais principale responsable des pertes.
Modèles de la bobine réelle
La bobine idéale est modélisée par une auto-inductance notée généralement L.
Mais la bobine réelle (particulièrement si elle est bobinée autour d'un matériau ferromagnétique) est un dipôle complexe possédant de nombreux paramètres et aussi le siège de phénomènes physiques dont certains sont la cause de non-linéarité (par exemple les phénomènes d'hystérésis).
Modèles à dipôles
Les modèles les plus simples et les plus fréquemment utilisés sont ceux correspondant à l'association d'une inductance et d'une résistance :
Modèle série
Il est constitué de l'association en série d'une inductance et d'une résistance :
Il correspond à l'équation
Modèle parallèle
Il est constitué de l'association en parallèle d'une inductance et d'une résistance :
Il correspond à l'équation
Équivalence entre les deux modèles
En régime sinusoïdal de fréquence f et de pulsation ω, les deux modèles précédents sont équivalents et interchangeables à condition de poser :
ou bien : 
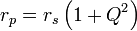
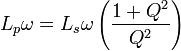
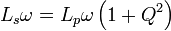
Avec 
: facteur de qualité de la bobine
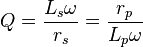
Modèles à trois dipôles
Aux modèles précédents, il est parfois nécessaire d'ajouter un condensateur en parallèle avec l'ensemble afin de rendre compte des effets capacitifs apparaissant entre les spires. Cette valeur de capacité est très faible mais elle devient prédominante à très grande fréquence.
Code de couleurs des bobines
Afin de déterminer l'inductance d'une bobine, il est parfois utilisé un code de couleur suivant ces normes :
| Couleur | 1. Anneau | 2. Anneau | 3. Anneau multiplicateur |
4. Anneau tolérance |
|---|---|---|---|---|
| "aucune" | — | — | — | ±20 % |
| argent | — | — | 10-2 µH | ±10 % |
| or | — | — | 10-1 µH | ±5 % |
| noir | 0 | 1 | 100 µH | — |
| marron | 1 | 1 | 101 µH | — |
| rouge | 2 | 2 | 102 µH | — |
| orange | 3 | 3 | 103 µH | — |
| jaune | 4 | 4 | 104 µH | — |
| vert | 5 | 5 | 105 µH | — |
| bleu | 6 | 6 | 106 µH | — |
| violet | 7 | 7 | 107 µH | — |
| gris | 8 | 8 | 108 µH | — |
| blanc | 9 | 9 | 109 µH | — |
| Couleur | 1. Anneau (large) |
2. à 4. Anneau chiffre |
5. Anneau multiplicateur |
6. Anneau tolérance |
|---|---|---|---|---|
| "aucune" | — | — | — | ±20 % |
| argent | Début | — | — | ±10 % |
| or | — | virgule | — | ±5 % |
| noir | — | 0 | 100 µH | — |
| marron | — | 1 | 101 µH | ±1 % |
| rouge | — | 2 | 102 µH | ±2 % |
| orange | — | 3 | 103 µH | — |
| jaune | — | 4 | 104 µH | — |
| vert | — | 5 | 105 µH | ±0,5 % |
| bleu | — | 6 | 106 µH | — |
| violet | — | 7 | 107 µH | — |
| gris | — | 8 | 108 µH | — |
| blanc | — | 9 | 109 µH | — |
| Le troisième chiffre est optionel. | ||||
Relation entre la tension et l'intensité
La tension uB aux bornes de la bobine et l'intensité i du courant sont reliés par l'équation différentielle :
où L est l'inductance de la bobine et r sa résistance propre (dans le cas d'une bobine parfaite, r = 0).
Comportement d'une bobine soumise à un échelon de tension
Lorsque la bobine est soumise brutalement à une tension constante E avec une résistance r en série, l'équation différentielle admet pour solution :
,
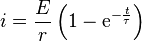
où 
est la constante de temps de la bobine.
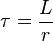
Démonstration mathématique
Si on admet que les solutions de l'équation différentielle sont de la forme i = A + BeCt où A,B,C sont constantes et t le temps écoulé, alors 
et l'équation devient :
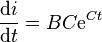
- E = LBCeCt + rA + rBeCt
puis :
- BeCt(LC + r) = E − rA.
Pour vérifier cette équation, il faut que LC + r = 0 et E = rA puisque eCt varie en fonction du temps.
On obtient alors :
et :
B peut alors prendre une infinité de valeurs. Ainsi, si la bobine est en charge, it = 0 = 0 d'où A + B = 0 et :
,
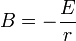
ce qui permet de trouver la solution de l'équation différentielle en i.
Démonstration des électriciens
la solution de l'équation différentielle :
est la somme de deux termes :
, la solution du régime libre correspondant à l'équation sans second membre 
, la solution du régime forcé correspondant au régime établi quand toutes les dérivées sont nulles et donc solution de 
.
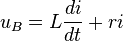
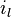
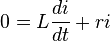
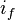
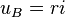
Solution du régime libre
Séparation des variables :
⇒ 
⇒ 
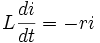
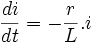
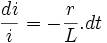
On intègre les deux membres
Si x = y alors 
donc
⇒ 
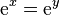
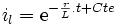
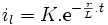
Solution du régime forcé
Lorsque la bobine est soumise à un échelon de tension 
la solution du régime forcé est :
.
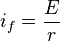
Solution de l'équation
.
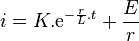
La détermination de la constante 
est faite grâce à la condition physique suivante : Le courant à travers une inductance ne peut en aucun cas subir de discontinuité.
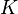
À l'intant 
, le courant vaut 
. On obtient l'équation :
⇒ 
Donc
.
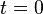
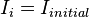
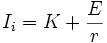
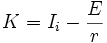
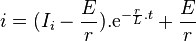
Souvent, dans les cas d'école, le courant initial est nul. On obtient alors :
Comportement en régime sinusoïdal
Pour obtenir les équations régissant le comportement d'une bobine réelle en régime sinusoïdal, il est nécessaire d'utiliser un des modèles décrit ci-dessus et de calculer l'impédance de la bobine soit en utilisant la représentation de Fresnel, soit en utilisant la transformation complexe.
Avec le modèle série, l'impédance de la bobine s'écrit :
ayant pour module : 
et pour argument : 
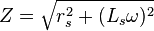
Du fait de son caractère inductif, l'intensité du courant sinusoïdal qui traverse la bobine soumise à une tension sinusoïdale présente un retard de phase 
par rapport à cette dernière. Ce retard est compris entre 0 et 90° (ou 0 et π /2 radians). On dit que le courant est en retard sur la tension.
Lorsque la bobine est réalisée autour d'un noyau ferromagnétique sans entrefer, les phénomènes de saturation magnétique et d'hystérésis entraînent des non-linéarités dans le comportement de la bobine : lorsqu'elle est soumise à une tension sinusoïdale, l'intensité du courant qui la traverse n'est pas purement sinusoïdal. Ces non linéarités sont très difficiles à prendre en compte. Elles sont souvent négligés en première approximation dans les calculs traditionnels.
Le dispositif élévateur de tension bobine
C'est un quadripôle qui met à profit le phénomène d'induction électromagnétique pour engendrer une pointe de courant sous une très haute tension. Elle constitue le système d'allumage du moteur à explosion à allumage commandé, autrement dit le moteur à essence.
Historique
Les physiciens français Antoine Masson et Louis Breguet en 1841 en firent les premiers essais. Dès 1836, Antoine Masson avait produit des courants sous haute tension en provoquant des interruptions rapides du courant produit par une pile. La bobine qu'il construisit en 1841 avec Breguet lui servit à produire des décharges dans des gaz raréfiés. Le mécanicien Ruhmkorff perfectionna le système pour les besoins de la physique expérimentale, on lui doit la Bobine de Ruhmkorff.
Principe
C'est une alimentation à découpage de type Flyback, c’est-à-dire deux circuits magnétiquement couplés dont l'un, appelé enroulement basse tension et comportant peu de spires est relié à l'alimentation alors que l'autre est connecté à l'utilisation. Ce deuxième enroulement comporte beaucoup de spires et porte généralemenrt de nom d'enroulement haute tension.
Le fonctionnement se fait en deux temps :
- Phase d'accumulation : L'énergie magnétique est préalablement stockée dans l'enroulement basse tension jusqu'à ce que la quantité d'énergie atteigne un optimum qui dépend du nombre de spire et du circuit magnétique.
- Phase de restitution : On ouvre brusquement le circuit primaire. L'énergie magnétique accumulée ne peut subir de discontinuité, force l'apparition d'un courant dans le deuxième enroulement sous une tension égale au produit de la tension primaire par le rapport des nombres de spires.