Base de Hilbert - Définition

Une base de Hilbert ou encore base hilbertienne est une généralisation aux espaces de Hilbert de la notion classique de base orthonormée en algèbre linéaire, pour les espaces euclidiens (ou hermitiens dans le cas complexe) de dimension finie.

Comme dans le cas des bases habituelles, il s'agit de pouvoir décomposer n'importe quel vecteur de l'espace en somme de vecteurs colinéaires à ceux de la famille choisie. Cependant dans le cas d'une base de Hilbert, on ne peut pas (généralement) écrire une égalité entre le vecteur décomposé et une combinaison linéaire finie des vecteurs de la base : on doit généralement se contenter d'une série dont les termes sont colinéaires aux vecteurs de la base, et convergeant vers le vecteur à décomposer (la notion de convergence d'une série a ici un sens car un espace de Hilbert est en particulier un espace vectoriel normé).

Définition

Soit H un espace de Hilbert de dimension infinie, et une famille de vecteurs de H. On dit que F est une base de Hilbert de H si :

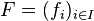
• F est une famille orthonormale de H, c'est-à-dire si :
  • ;
  • .
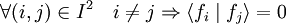
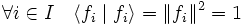
    Dans ce cas la famille est nécessairement libre.
• (la convergence de cette série étant au sens de la norme ).

Dans ce cas, la famille est unique pour chaque vecteur x ; ce sont ses coordonnées dans la base de Hilbert F. L'expression des coordonnées est .

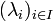
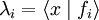
Propriétés

Ainsi une base de Hilbert de H n'est pas une base de H, mais une base orthonormale d'un sous-espace D, qui est dense dans H et qui permet donc d'approcher tous les éléments de H.

Théorème 2 (identité de Parseval) – Une famille orthonormale de H est une base de Hilbert si et seulement si : .

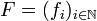
Dans ce cas, on a aussi .

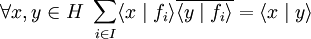
C'est une généralisation du théorème de Pythagore, bien connue dans le cadre des séries de Fourier.

Un cas important est celui où l'ensemble I est dénombrable. On dit alors que l'espace de Hilbert est séparable. On peut alors supposer que ou . Le théorème 2 a pour conséquence que tout espace de Hilbert séparable est isomorphe à l'espace des suites telles que converge.

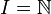
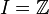
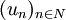
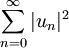
La démonstration de ce dernier théorème nécessite l'axiome du choix.

On notera que dans un espace vectoriel de dimension infinie, une base de Hilbert B n'est jamais une base dudit espace vectoriel: un vecteur n'est pas en général une combinaison linéaire finie d'éléments de cette base B.

Exemples

L'exemple classique de base de Hilbert (et même l'origine du concept) est l'ensemble des fonctions trigonométriques cos(nx) et sin(nx), pour l'espace de Hilbert L²([0,2π]) (voir les espaces L^p). Cependant, en termes d'algèbre linéaire pure, la famille des fonctions cos(nx) et sin(nx) n'est pas une base car non génératrice. Précisément, c'est une base du sous-espace des polynômes trigonométriques. Notons qu'il est beaucoup plus commode de travailler avec des fonctions à valeurs complexes, et d'utiliser la base e^inx