Théorème d'Ascoli - Définition
En analyse fonctionnelle, le théorème d'Ascoli est un puissant résultat caractérisant les parties relativement compactes de l'espace des fonctions continues définies sur un espace métrique compact à valeurs dans un espace métrique complet (espace vectoriel normé complet). Il se généralise sans difficulté aux espaces topologiques localement compacts, localement séparables, et dénombrables à l'infini.
Ce théorème est connu pour son nombre considérable d'applications (complétude de certains espaces fonctionnels, compacité de certains opérateurs, dépendance en les conditions initiales dans les équations différentielles ...).
Énoncé
Dans un espace vectoriel normé de dimension finie, les parties compactes sont exactement les parties fermées et bornées. Dans un espace vectoriel topologique séparé, les parties relativement compactes restent bornées ; mais la réciproque est fausse. Le théorème d'Ascoli traite du cas de l'espace des fonctions continues :
Soient
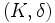
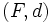
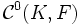
Une partie A de
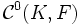
- A est équicontinue, i.e pour tout
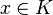
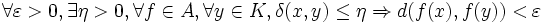
- Pour tout
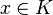
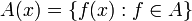
Un ensemble de fonctions r-lipschitziennes est un exemple d'ensemble équicontinu.
Il existe de nombreuses variantes du théorème d'Ascoli.
Démonstration
Le théorème d'Ascoli établit une équivalence. Les deux implications sont démontrées séparément. Les notations sont celles de l'énoncé ci-dessus.
Condition nécessaire
Supposons que A soit relativement compact. Comme
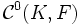
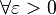
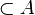
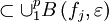
Littéralement, toute fonction f dans A se trouve à une distance au plus ε de l'un des fj. Pour x fixé dans K, toute image f(x) se trouve donc à une distance au plus ε de l'un des fj(x). De fait :
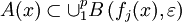
Une telle inclusion étant valable pour tout
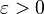
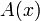
En outre, les fonctions fj sont continues sur le compact
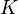
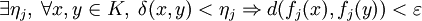
Posons
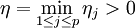
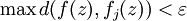
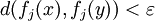
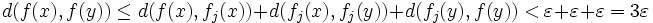
Cette inégalité, vérifiée par tous x et y tels que d(x,y) < η, reste valable pour toute fonction
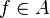
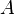
Condition suffisante
La réciproque est le sens le plus souvent utilisé et demande plus d'attention. On souhaite démontrer qu'une partie équicontinue A de C0(K,F) telle que A(x) soit relativement compacte pour tout x, est relativement compacte. Comme C0(K,F) est un espace métrique, il revient au même d'établir que l'adhérence de A est séquentiellement compacte ; ou encore que toute suite d'éléments de l'adhérence de A admet au moins une valeur d'adhérence.
Soit donc
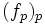

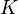
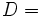
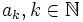
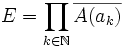
Par hypothèses,
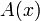
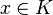
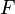

A chaque
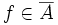
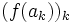

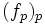
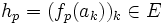
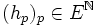
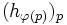
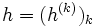
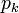
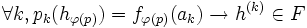
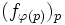
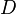
De plus,
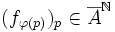
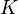
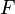
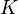
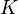
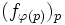
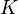
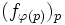
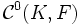
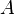
Opérateurs à noyau
| Théorèmes de l'analyse fonctionnelle |
| Théorème d'Ascoli | Théorème de Baire | Théorème de Banach-Alaoglu | Théorème de Banach-Mazur | Théorème de Banach-Schauder | Théorème de Banach-Steinhaus | Théorème du graphe fermé | Théorème de Hahn-Banach |

















































