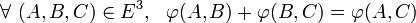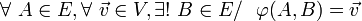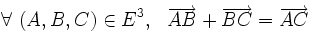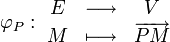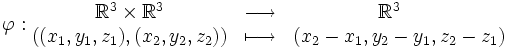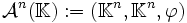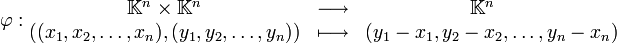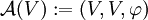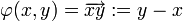Espace affine - Définition
Historiquement, la notion d’espace affine est issue du choc dû à la découverte de nouvelles géométries parfaitement cohérentes, mais différant de celle d'Euclide par l'axiome des parallèles. Elles remettaient en cause les notions de longueur et d'angle, qui reposaient elles-mêmes sur celle de distance, et poussèrent à redéfinir l'espace euclidien, en excluant ces notions et tout ce qui s'y rapportait. Le résultat fut une géométrie affine, où l'espace apparait comme une structure algébrique, voisine de celle d'espace vectoriel qui en fut dégagée par la suite (donnant ainsi naissance à l'algèbre linéaire).
Définitions
Il existe de nombreuses manières de définir un espace affine (voir l'article " Structure affine "). Ici, nous supposons donnés :
- un corps (
, + , x ) , noté " " en abrégé, d'éléments neutres " 0 " pour la loi additive et " 1 " pour la loi multiplicative ;
- les éléments du corps sont habituellement appelés " scalaires " et notés par des lettres grecques minuscules :
,...
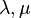
- un espace vectoriel (
, 
, · ) sur ce corps, noté " " en abrégé, d'élément neutre " 
" ;
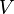
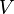
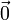
- les éléments de l'espace vectoriel sont appelés " vecteurs " et notés par des lettres latines minuscules surmontées d'une flèche :
, 
,...
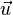
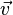
- et un ensemble
non vide, à partir duquel nous allons construire notre espace affine ;
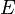
- ses éléments seront appelés " points " et notés par des lettres latines majuscules :
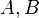
,... - remarque : les couples d'éléments de , éléments de
, seront appelés " bipoints ", conformément à la tradition. De même, le premier élément d'un tel couple sera appelé " origine " du bipoint, et le second élément " extrémité " du bipoint.
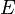
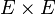
Un espace affine peut alors être défini comme le triplet 
où 
est une application satisfaisant aux deux propriétés suivantes (appelées axiomes des espaces affines) :
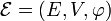
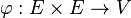
- (A1) Pour tout couple de bipoints tels que l'origine du second coïncide avec l'extrémité du premier, la somme des images par
est égale à l'image, toujours par , du bipoint formé par l'origine du premier et l'extrémité du second. En d'autres termes :
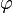
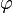
- (A2) Pour tout point et tout vecteur, il existe un unique bipoint dont l'origine est le point considéré et dont l'image par est le vecteur considéré. En d'autres termes :
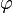
Notation : pour tout couple de points 
, et si toute confusion est impossible, on note " 
" le vecteur 
.
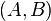
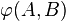
La propriété (A1) s'écrit alors :
Cette propriété est souvent appelée Relation de Chasles.
La propriété (A2) dit tout simplement que lorsqu'on fixe un point 
dans , l'application 
:
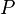
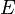
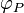
est une bijection. Elle permet aussi de définir une opération (qui est plus utilisée comme une notation) correspondant à l'addition d'un vecteur à un point :
-
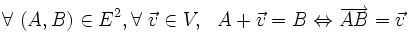
La dimension d'un espace affine est la dimension de l'espace vectoriel qui lui est associé.
L'espace vectoriel est appelé direction de
Propriétés élémentaires
Les propriétés suivantes découlent directement de la définition d'espace affine (c'est-à-dire des axiomes (A1) et (A2)). Soient 
et 
des points quelconques dans un espace affine 
. Nous avons alors :
;
;
(relation de Chasles généralisée)
(relation du parallélogramme).
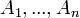
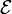
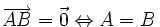
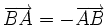
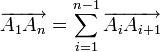
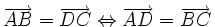
Exemples d'espaces affines
- Regardons le plan
comme un ensemble de points (sans structure particulière) mais aussi comme un 
-espace vectoriel.
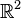
- Le triplet
où est définie par : -
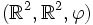
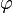
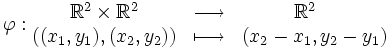
est un espace affine de dimension 2 (c'est le plan affine).
- Le triplet
avec :
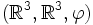
est un espace affine de dimension 3.
- De façon plus générale, si est un corps quelconque, l'espace affine canonique sur de dimension n est le triplet :
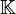
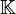
où 
est vu à la fois comme un espace de points et un -espace vectoriel, et l'application 
est définie par :
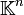
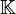
- De façon encore plus générale, si V est un espace vectoriel sur un corps , on définit l'espace affine canonique associé à l'espace vectoriel V par le triplet :
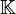
où V est vu à la fois comme un espace de points et un -espace vectoriel, et l'application est définie par :
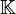
Sous-espaces affines
Un sous-espace affine d'un espace affine est un triplet 
où 
est inclus dans et 
est un sous-espace vectoriel de , le tout satisfaisant aux deux propriétés suivantes :
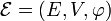
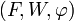
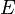
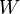
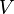
- (SA1) Pour tout couple de points
et 
de , le vecteur appartient à ;
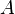
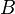
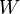
- (SA2) Pour tout point de et tout vecteur
de , le point 
appartient à .
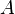
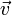
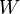
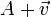
Le sous-espace vectoriel est appelé la direction du sous-espace affine. La dimension d'un sous-espace affine est tout simplement la dimension de sa direction.
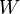
On nomme Hyperplan affine un sous-espace affine dont la direction est un hyperplan de V.
Tout hyperplan affine peut se définir comme ensemble des points 
vérifiant une équation f(M) = 0, où f est une forme affine, c'est-à-dire une application affine dont la partie linéaire est une forme linéaire.
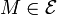
Notion de parallélisme
Dans un espace affine , deux sous-espaces affines et 
sont parallèles si l'un des sous-espaces vectoriels, ou 
, est inclus dans l'autre.
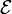
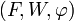
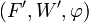
Le célèbre cinquième postulat d'Euclide n'est alors qu'un résultat facile à démontrer à partir des définitions et des propriétés des espaces vectoriels :
Théorème (Cinquième Postulat D'Euclide) : Dans un espace affine , étant donné un point quelconque et une direction , il existe un unique sous espace affine passant par et ayant comme direction.
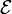
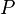
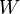
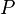
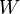
A voir aussi...
- La notion d'application et de transformation affine,
- La définition de géométrie affine,
- La notion de repère affine.