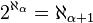Hypothèse du continu - Définition
En théorie des ensembles, l'hypothèse du continu, due à Georg Cantor, affirme qu'il n'existe aucun ensemble dont le cardinal est strictement compris entre le cardinal de l'ensemble des entiers naturels et celui l'ensemble des nombres réels. Reformulé sous une autre forme : Tout ensemble strictement plus grand (au sens du cardinal) que l'ensemble des entiers naturels doit contenir une " copie " de l'ensemble des nombres réels. Les mathématiciens lui vouent une importance certaine, puisqu'elle est le premier problème des 23 problèmes de Hilbert.
Cantor, en mettant en place la théorie axiomatique des ensembles, définit les cardinaux des ensembles infinis, qu'il appela alors nombres transfinis, dans le but de comparer les différents infinis. Au fur et à mesure de la formation de sa théorie, il en vint à comparer les cardinaux de


Définition de l'hypothèse du continu
On définit
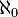

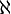

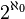
Soit
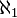
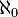
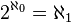


Cardinalité
Deux ensembles S et T ont même cardinalité lorsqu'il existe une bijection
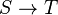
Par exemple, les ensembles {avion, moto, sous-marin} et {air, terre, eau} ont même cardinalité. En fait, la nature des objets mis en jeu n'a aucune importance ; leur symbolique ne sert qu'à aider le lecteur à suivre le discours.
Avec des ensembles infinis, certaines analogies peuvent tromper. Naïvement, il semble y avoir plus de nombres rationnels que de nombres entiers : un rationnel est le quotient de deux entiers. Cependant, cette vision est erronée, car il est possible d'énumérer tous les rationnels en les indexant par les entiers naturels. L'ensemble des nombres rationnels, noté


L'ensemble des nombres réels, noté



L'hypothèse du continu affirme que tout sous-ensemble du continuum est soit fini, soit infini dénombrable, soit a la même cardinalité que le continuum.
Indécidabilité
Kurt Gödel a montré en 1938 que l'ajout de l'hypothèse du continu à la théorie des ensembles, défini par exemple par les axiomes de Zermelo-Fraenkel, ne changeait nullement la consistance de cette théorie, même si on l'augmente de l'axiome du choix.
Paul Cohen a montré en 1963 que l'hypothèse du continu n'était pas démontrable dans la théorie des ensembles basée sur les axiomes de Zermelo-Fraenkel. Elle est donc indépendante de la théorie des ensembles.
Commencée il y a une trentaine d'années, la recherche d'axiomes " naturels " à ajouter à la théorie de Zermelo-Fraenkel (axiomes de détermination, axiomes de grands cardinaux, etc.) va sans doute permettre, grâce aux travaux de Woodin, de résoudre prochainement l'hypothèse du continu... par la négative, ce que soupçonnait déjà Gödel.
Il n'y a pas de quoi être surpris de l'existence d'énoncés ne pouvant être démontrés ou infirmés à partir d'un système d'axiomes donné, c'est par exemple le cas du postulat d'Euclide relativement à son système "axiomatique".
L'hypothèse du continu n'est pas sans rapport avec des énoncés d'analyse, ou de théorie de la mesure.
Historiquement, les mathématiciens en faveur d'une large classe d'ensembles rejettent l'hypothèse du continu, alors que ceux favorables au contraire à une ontologie ensembliste plus restreinte l'acceptent.
Généralisation
L'hypothèse généralisée du continu déclare qu'il n'existe pas d'ensemble dont le cardinal serait strictement compris entre
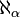
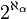
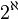
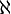
On aurait alors