Démonstration (mathématiques élémentaires) - Définition
Cet article fait partie de la série Mathématiques élémentaires |
| Algèbre |
| Analyse |
| Arithmétique |
| Géométrie |
| Logique |
| Probabilité |
| Statistique |
Démontrer une propriété c'est utiliser des théorèmes, des définitions ou des axiomes que l'on sait être vrais et quelques règles de logique élémentaire.
Elle expose une justification d’une propriété nouvelle algébrique, géométrique, numérique… Une démonstration est rarement achevée parce qu’on peut toujours retoucher son style de rédaction (plus ou moins télégraphique), sa longueur (profondeur des détails), les outils utilisés (parfois radicalement différents) voire simplement l’usage des règles logiques. Certains s’amusent même à s’interdire l’usage d’une lettre, d’une méthode ou même de mots pour écrire une preuve.
Du point de vue pédagogique, une démonstration sert à prouver aux élèves que le professeur a raison, mais aussi qu’un autre professeur que lui aurait aussi raison, à condition d’accepter les prérequis et la méthode de la preuve. Elle sert aussi à montrer aux élèves la liberté scientifique dans l’acte de rédiger et d’expliquer.
Quelques méthodes de démonstration
En mathématiques, il existe plusieurs méthodes pour démontrer un théorème :
- Par application directe du théorème
- Par contraposée
- Par l’absurde
- Par analyse-synthèse
- Par l’exemple
Par application directe du théorème
Si un théorème est sous la forme Si A alors B, s’il est vrai et si on montre que A est vraie alors B est vraie.
Ainsi pour démontrer que le triangle ABC est rectangle, avec AB=12, BC=13 et AC=5, on utilise le théorème réciproque de Pythagore :
- On vérifie d’une part que AB²+AC²=12²+5²=144+25=169 et d’autre part que BC²=13²=169 donc AB²+AC²=BC²
- Le théorème réciproque de Pythagore énonce que Si le carré du côté d'un triangle est égal à la somme des carrés des deux autres côtés alors ce triangle est rectangle (l'hypoténuse étant le premier côté cité)
- On a bien A vraie et si A alors B vraie, on peut donc en conclure que B est vraie, soit que le triangle ABC est rectangle en A
Par contraposée
Pour démontrer que " Si A alors B " est vrai, il est souvent commode de démontrer que la contraposée est vraie
Par l'absurde
Pour montrer que A est vraie, on montre que si on suppose A est fausse on arrive alors à une contradiction.
Exemple:
A : Il existe une infinité de nombres premiers
non A : Il existe un nombre fini de nombres premiers
On les note
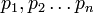
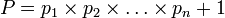
P n'est divisible ni par p1, ni par
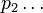
Or P est premier car tout nombre non premier admet au moins 1 diviseur premier.
Mais il n'y a pas de nombre premier plus grand que pn d'après l'hypothèse. Donc A est vraie.
Par analyse-synthèse
On suppose le problème résolu, on en déduit les conditions nécessaires (phase d'analyse). On utilise ces conditions nécessaires pour résoudre le problème (phase de synthèse).
Exemple :
Toute fonction définie sur ? est la somme d'une fonction paire et d'une fonction impaire
Analyse
Si f=p+i avec p fonction paire et i fonction impaire
- Quel que soit x ∈ ?, f(x)=p(x)+i(x) et f(−x)=p(x)−i(x)
- p(x)=(f(x)+f(−x))/2 et
- i(x)=(f(x)−f(−x))/2
Synthèse
On considère les fonctions i et p définies par les formules précédentes
- f=p+i
- Quel que soit x ∈ ?, p(−x)=p(x) donc p est paire
- Quel que soit x ∈ ?, i(−x)=−i(x) donc i est impaire
Par l’exemple
Pour montrer que pour un x, P(x) est vraie, on trouve une valeur a telle que P(a) soit vraie : on trouve un exemple.
Pour montrer que pour un x, P(x) est fausse on montre qu'il existe x tel que non P(x) est vraie. On trouve a tel que non P(a) soit vraie : un contre-exemple.
Attention
Pour montrer que pour tout x, P(x) est vraie, un exemple ne suffit pas bien au contraire.

















































