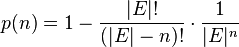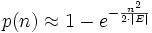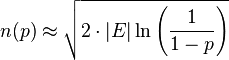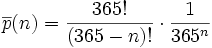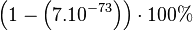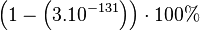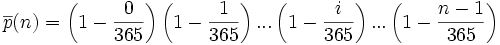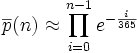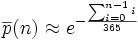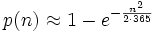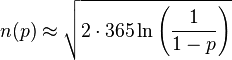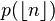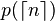Paradoxe des anniversaires - Définition
Le paradoxe des anniversaires, dû à Richard von Mises, est à l'origine, une estimation probabiliste du nombre de personnes que l'on doit réunir pour avoir une chance sur deux que deux personnes de ce groupe aient leur anniversaire le même jour. Il se trouve que ce nombre est 23, ce qui choque un peu l'intuition. À partir d'un groupe de 57 personnes, la probabilité est supérieure à 99 %.
Cependant, il ne s'agit pas d'un paradoxe dans le sens de contradiction logique ; c'est un paradoxe, dans le sens où c'est une vérité mathématique qui contredit l'intuition : la plupart des gens estiment que cette probabilité est très inférieure à 50 %.
Les gens pensent en général à la probabilité que 2 personnes soient nées en même temps un jour donné, probabilité qui est en effet très faible.
Généralisation
Ce paradoxe des anniversaires se généralise bien évidemment à la situation plus abstraite que l'on peut énoncer sous la forme :
Soit E un ensemble fini. La probabilité p(n) que, parmi n éléments de E, chaque élément étant tiré uniformement dans tout l'ensemble E, deux éléments au moins soient identiques vaut :
où la notation | E | désigne le cardinal de l'ensemble E.
Une valeur approchée est donnée par
et une valeur de n en fonction de p par
Démonstration
Nous donnons une preuve pour le cas d'origine, avec des jours d'anniversaires, mais cela se transpose simplement au cas de la généralisation énoncé.
Le plus simple pour obtenir le résultat annoncé est de calculer la probabilité que chaque personne ait un jour anniversaire différent de celui des autres. On va procéder par dénombrement, c'est-à-dire, que nous allons compter le nombre de cas où n personnes ont des jours d'anniversaires différents et nous diviserons par le nombre de possibilités. Il y a n personnes, pour chacune il y a 365 jours possibles, donc au total si on ne se fixe aucune contrainte, il a 365n possibilités. Si maintenant on veut des jours différents, nous obtenons un arrangement de n parmi 365, soit :
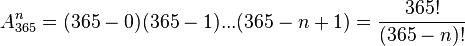
On a donc
Or, l'évènement " un jour anniversaire différent par personne " est le complémentaire de " au moins deux identiques ". Par conséquent la probabilité recherchée est
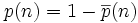
En faisant l'application numérique, on trouve 50,72 % pour 23 personnes … Le calcul exposé néglige la date du 29 février dont la prise en compte changerait très peu le pourcentage indiqué.
| n | p(n) |
|---|---|
| 10 | 12% |
| 20 | 41% |
| 30 | 70% |
| 50 | 97% |
| 100 | 99.99996% |
| 200 | 99.9999999999999999999999999998% |
| 300 |
|
| 350 |
|
| ≥366 | 100% (par le Théorème des tiroirs) |
Approximation
p(n)
La probabilité
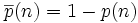
Or, on a le développement limité ex = 1 + x + o(x) pour x voisin de 0. Cela conduit à l'approximation :
Or, la somme des entiers de 0 à n − 1 vaut (n − 1)n / 2, ce qui donne finalement :
En revenant à p(n) :
n(p)
L'approximation de p(n) permet d'obtenir simplement une approximation du nombre de personnes nécessaire pour avoir une probabilité donnée p d'avoir au moins deux personnes avec le même jour d'anniversaire. On obtient ainsi
Quelques valeurs numériques
Le tableau ci-dessous indique, pour une probabilité p, l'approximation n(p), puis, sur la même ligne, l'approximation de la probabilité pour l'entier inférieur ou égal à n(p) (noté
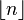
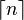
| p | n |
|
|
|
|
|
0.01
|
2.70864
|
2 | 0.00274 | 3 |
0.00820
|
| 0.05 | 6.11916 | 6 | 0.04046 | 7 | 0.05624 |
|
0.1
|
8.77002
|
8 | 0.07434 | 9 |
0.09462
|
|
0.2
|
12.76302
|
12 | 0.16702 | 13 |
0.19441
|
| 0.3 | 16.13607 | 16 | 0.28360 | 17 | 0.31501 |
| 0.5 | 22.49439 | 22 | 0.47570 | 23 | 0.50730 |
| 0.7 | 29.64625 | 29 | 0.68097 | 30 | 0.70632 |
| 0.8 | 34.27666 | 34 | 0.79532 | 35 | 0.81438 |
| 0.9 | 40.99862 | 40 | 0.89123 | 41 | 0.90315 |
| 0.95 | 46.76414 | 46 | 0.94825 | 47 | 0.95477 |
|
0.99
|
57.98081
|
57 |
0.99012
|
58 | 0.99166 |
Applications
Le paradoxe des anniversaires est utilisé en cryptographie pour élaborer des attaques sur les fonctions de hachage. Une des contraintes imposées sur ces fonctions, pour une utilisation cryptographique, est de produire peu de collisions, autrement dit, de rarement prendre la même valeur sur des entrées différentes.
Le paradoxe des anniversaires donne une borne sur le nombre moyen d'éléments nécessaires pour avoir une collision avec une probabilité
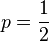
Plus concrètement, si une fonction de hachage a une sortie de N bits alors l'ensemble d'arrivée possède 2N éléments et il faut environ |2N/2 hachés d'éléments distincts pour produire une collision avec 50% de chance ; les sorties de la fonction pouvant être comparées à des personnes avec des anniversaires se répartissant sur 2N valeurs.