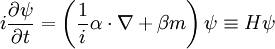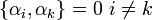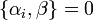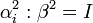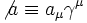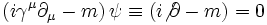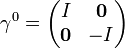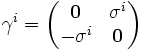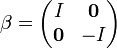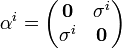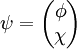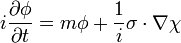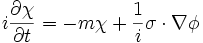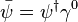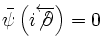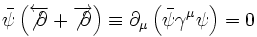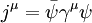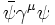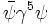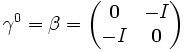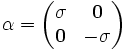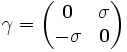Matrice de Dirac - Définition

Les matrices de Dirac sont des matrices qui furent introduites par Paul Dirac, lors de la recherche d'une équation d'onde relativiste de l'électron.

Intérêt

La généralisation naturelle de l'équation de Schrödinger est l'équation de Klein-Gordon. Malheureusement, celle-ci décrit des particules de spin 0 et ne convient pas pour les électrons qui sont de spin 1/2. Dirac essaya alors de trouver une équation linéaire comme celle de Schrödinger sous la forme :

où ψ est une fonction d'onde vectorielle, m la masse de la particule, H l'hamiltonien et sont respectivement un vecteur de matrices hermitiques et une matrice hermitique. L'équation de Dirac doit respecter les trois points suivants :

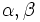
• Les composantes de ψ doivent satisfaire l'équation de Klein-Gordon, une onde plane dont une solution est :

  étant une solution.

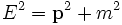
• Il existe un quadrivecteur densité de courant qui est conservé et dont la composante temporelle est une densité positive (identifiée avec la charge électrique).
• Les composantes de ψ ne doivent satisfaire aucune condition auxiliaire, c’est-à-dire qu'à un instant donné elles sont des fonctions indépendantes de x.

Matrices de Dirac

Dirac proposa que les matrices hermitiques soient anticommutantes et de carré égal à un. C’est-à-dire qu'elles obéissent à l'algèbre suivante :

où les crochets sont l'anticommutateur .

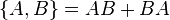
En élevant l'équation de Dirac au carré, on vérifie immédiatement que la première condition est satisfaite. On introduit ensuite les matrices de Dirac γ^μ proprement dites :

γ⁰ = β

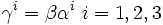
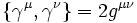
Le slash de Feynman

On introduit aussi le " slash " de Feynman :

L'équation de Dirac prend alors la forme :

Une représentation explicite, dite " représentation standard ", est donnée par :

où I est la matrice unité 2×2 et σⁱ sont les matrices de Pauli.

Cette représentation est particulièrement pratique car elle met en évidence le caractère spinoriel (dû au spin demi-entier) de la fonction d'onde de l'électron et elle sépare les composantes d'énergie positive et négative. Ainsi, en écrivant la fonction d'onde comme un bispineur :

où φ et χ sont deux spineurs, l'équation de Dirac devient :

En introduisant la fonction d'onde conjuguée comme :

On trouve :

Et avec l'équation de Dirac, cela donne :

Ce qui donne un courant conservé :

Dont la composante temporelle est positive. On définit aussi la matrice :

γ⁵ = γ⁰γ¹γ²γ³

L'utilisation de γ⁵ permet ainsi de construire différents types de combinaisons tel que, par exemple, des vecteurs :

Des pseudoscalaires :

On vérifie aisément la covariance relativiste de tout ce formalisme.

Représentations

Les matrices de Dirac sont totalement déterminées par la relation :

γ^μγ^ν + γ^νγ^μ = 2η^μν

où η^μν est le tenseur de Minkowski. On a aussi γ_μγ^μ = 4. Il existe une infinité de représentations possibles des matrices de Dirac. C’est-à-dire une infinité de solutions possibles à la relation précédente.

Citons par exemple la représentation de Majorana obtenue à partir de la représentation précédente en échangeant α₂ et β et en changeant le signe de α₁ et α₃. Elle a la propriété intéressante de rendre l'équation de Dirac réelle dont les solutions sont des combinaisons de solutions réelles. Citons aussi la représentation chirale :

Son avantage est que les deux spineurs se transforment indépendamment sous les rotations et les translations. Elle est particulièrement utile pour des particules sans masse, les équations se simplifiant considérablement. Elle a été utilisée pour le neutrino bien que l'on sache maintenant que celui-ci possède une masse extrêmement petite mais non nulle.

Bibliographie

• Lev Landau, Evguéni Lifchitz, Physique théorique, t. 4 : Électrodynamique quantique, Éditions MIR, Moscou, [détail des éditions]

• C.Itzykson, J.B.Zuber Quantum Field Theory
• N.Nelipa Physique des particules élémentaires