Balistique extérieure - Définition
La liste des auteurs de cet article est disponible ici.
Le cas assez réaliste : résistance en v²
Alors , encore une fois , toutes les trajectoires s'expriment à l'aide du seul paramètre k = (Vo/V1)².sinAo . L'hodographe se calcule, mais sans propriété simple, à part sa non-symétrie.
- En fait, en pratique, on recourt à des abaques.
{ L'empirisme le plus total ( ???) montre que la portée est : pour z=0 , x = Portée(k=0)/( k +0.5exp(-2k/3)). (1+ résidu(k)), avec résidu(k)< 0.0025.(Cet empirisme des artilleurs est conforté par le fait que le résultat est bon pour k petit et pour k grand?)}
Le cas irréaliste linéaire
Ce cas est totalement irréaliste, mais il est étudié simplement parce qu'il est facilement intégrable !!!
Il donne, par le tracé des trajectoires, une certaine intuition du mouvement, considéré par beaucoup comme fausse.
L'équation différentielle est :
|
|
L'hodographe est donc la droite:
|
|
la trajectoire du projectile P est :
|
|
{ébauche : aide figure demandée, svp }
La trajectoire est dissymétrique par rapport à son point de culmination : pour la même altitude positive, il y a deux racines dont la demi somme décroît régulièrement, et les angles A1 et A2 ont une somme négative.
- remarques annexes :
- Pour t < \tau, on retrouve la trajectoire parabolique + termes perturbatifs :
|
|
.
- L'hodographe peut se retrouver en polaire via l'équation-Balistique ( bien que cela soit inutilement compliqué ! ) : l'équation est 2-Bernoulli, on prend donc T(A) = g\tau.1/v comme fonction inconnue et l'équation se simplifie : -dT/dA = T. tan(A) +1/cos(A) ( +CI) eq dif linéaire dont la solution est : T(A) = g \tau . 1/v = sin(A) + cos(A) [ (gt/Vo -sin(Ao))/cos(Ao)] : l'hodographe est bien un segment de droite.
Histoire des sciences
Il est clair que depuis le temps des frondes, flèches, arbalètes, catapultes, onagres, ballistes, pierrières, trébuchets, scorpions, puis arquebuses, mousquets, canons (Chute de Byzance,1453), la balistique extérieure a suscité de nombreuses recherches.
L'artillerie développe énormément la recherche. Donc en Europe de 1500 à 1638, un effort prodigieux est mené, pour performer l'enseignement d'Aristote. Tartaglia a une solution fausse, mais proche de la réalité avec la notion d'asymptote.
- Ce sont Galilée et Torricelli qui mettent définitivement en forme le mouvement de chute libre avec lancer, au grand dam des artilleurs : Torricelli a historiquement complètement traité ce problème dans le vide (cf : parabole de sûreté). Mais il savait fort bien que sa description ne s'accordait pas à celle des artificiers (à cause de la résistance de l'air).
- Il faut attendre Newton pour avoir vraiment le développement de la théorie ; puis Bernoulli pour mettre en forme ce qui sera nommé la balistique extérieure. En particulier pour invalider cette hérésie du calcul de Torricelli qui donnait une portée infinie pour un angle A = -90°.
- Ensuite, le calcul porte soit sur des améliorations numériques, soit sur des cas d'intégrations spéciaux, œuvres plutôt de mathématiciens : la balistique extérieure a connu son apogée vers les années 1910 ; aujourd'hui, les calculs sont conduits souvent par ordinateur.
- Néanmoins, l'effort le plus grand aura été opéré par Galilée : cette idée osée d'imaginer la trajectoire dans un fluide évanescent ; d'analyser l'impetus de départ ; de voir qu'il ne s'épuisait jamais ; mais qu'au contraire la chute libre était "composition" des mouvements Vo.t et 1/2 g.t², et que le Vo de départ pouvait être compté comme rien, etc, etc, efforts amplement racontés dans les Dialogues de 1632 et les Discours de 1638.
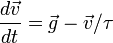
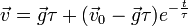
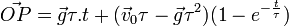
![^{\vec {OP} = \vec v_0 t + \frac 1 2 \vec g t^2 - [ \vec v_0 t^2/2\tau + \vec g t^3/6 \tau^2] +...}](https://static.techno-science.net/illustration/Definitions/autres/3/377dd9719b9ab194035b0f66e5e785c3_a5b37bdfab6e167a77c5d3e1264bbf05.png)

















































