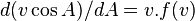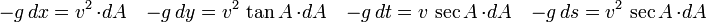Balistique extérieure - Définition

Introduction

La balistique extérieure est la branche de la balistique qui étudie le vol libre des projectiles sans propulsion interne. Le cas d'application le plus important est l'étude de la trajectoire des balles ou obus tirés par une arme à feu après qu'ils ont quitté le canon de l'arme.

Mouvement ; asymptote

Le cas d'un point matériel soumis à un champ de pesanteur uniforme tombant sans vitesse initiale est traité dans l'article Chute avec résistance de l'air. Il a fait apparaître la notion très importante de vitesse-limite. De même dans le cas d'un projectile, il apparaît la notion d'asymptote de la trajectoire.

La restriction champ de pesanteur uniforme est gardée ici ; si la trajectoire du mobile dépasse 100km, il faut modifier.

Le vecteur vitesse sera repéré par son module v et son angle de hauteur A : les composantes cartésiennes sont donc .

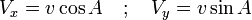
L'analyse des forces est : poids et résistance fluide de module r(v): = mg f(v), de direction opposée à la vitesse.

Hodographe

L'accélération montre que la courbe est concave vers le bas : donc, quand l'abscisse curviligne s augmente, l'angle de la vitesse avec l'horizontale, A(t) diminue de sa valeur initiale Ao à -90° : la fonction t-> - A(t),fonction croissante monotone, peut être avantageusement choisie comme échelle de temps:

échelle des temps

• Les équations de Frenet donnent :
• dv/dt = -g sinA -g.f(v)
• mv²/R = mg cosA soit -v.dA/dt = g cosA.

d'où l'échelle de temps : dt = -V(A)/(g cosA).dA

On en tirera dx = -v²/g .dA ; dy =dx.tanA pour avoir la trajectoire, dont les coordonnées intrinsèques sont R = V²(A)/(g.cosA) ;

équation dite hodographe de la balistique

En éliminant dt :

équation du premier ordre, avec C.I. de Cauchy ( Ao, Vo).

D'où v = V(A), ce qui est l'hodographe en coordonnées polaires.

Quand A tend vers -90°,développer la dérivée, v tend vers une limite V1 telle que :

On retrouve la notion de vitesse-limite de l'article chute avec résistance de l'air.

La trajectoire

Pour obtenir la trajectoire, il suffit donc d'intégrer l'équation précédente, puis :

Tout s'exprime donc "à une quadrature près" si on sait résoudre l'équation de l'hodographe (Bernoulli, 1695).

Cette trajectoire est dissymétrique par rapport à sa culmination (qui correspond à A = 0), car l'équation (B) donne v(A) > v(-A) et x(t) représente l'aire balayée par l'hodographe (cf. vitesse aréolaire).

asymptote de la trajectoire

L'immense différence avec le cas de Torricelli est que :

• la vitesse est bornée par V1 et ne croît donc pas indéfiniment.
• et x est fonction croissante du temps mais majorée par V1²/g .Pi/2 donc bornée : la portée est finie, quelle que soit la "hauteur de la citadelle" : c'est bien ce qu'affirmaient les artilleurs, la trajectoire parabolique de Torricelli n'étant solution valable que dans le cas irréaliste où l'on néglige la résistance de l'air.

Cas intégrables

L'équation (B) de l'hodographe est donc l'équation fondamentale de la Balistique.

• Le cas le plus facile d'intégrabilité est donné par Lagrange : f(v) = kv^n = (v/V1)^n . L'équation (B) est alors une équation de Bernoulli, et s'intègre comme telle ( on obtient une équation différentielle linéaire, du premier ordre ).
• Drach(CRAS1914) donne les différentes formes de f(V) pour lesquelles l'intégration est possible, y compris via les fonctions elliptiques.
• En pratique, les artilleurs préfèrent une intégration numérique de (B), compte-tenu de la formule empirique de f(V) déterminée en soufflerie ; il faut en effet tenir compte de la variation de la densité de l'air avec l'altitude, donc en réalité f(V)*d(z), ce qui est plus dur à résoudre.

Enfin , pour les tirs assez lointains, il ne faut pas oublier la déviation de Coriolis ( cf la Grosse Bertha).