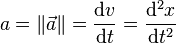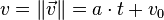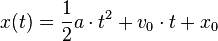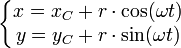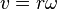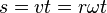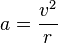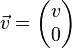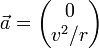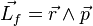Cinématique - Définition

Mouvement simple

Le problème est donc ramené à trouver la fonction donnant la position sur la courbe en fonction du temps, soit s(t). On appelle diagramme horaire le graphe de [t,s(t)] : de tels diagrammes sont très utilisés pour les trains (par exemple en France, le CHAIX donne pour l'ensemble du réseau les diagrammes horaires, ce qui permet de calculer les tableaux de correspondance de transport de gare en gare).

Mouvement rectiligne

Evolution de la position, de la vitesse et de l'accélération d'un corps dans un mouvement rectiligne uniforme.

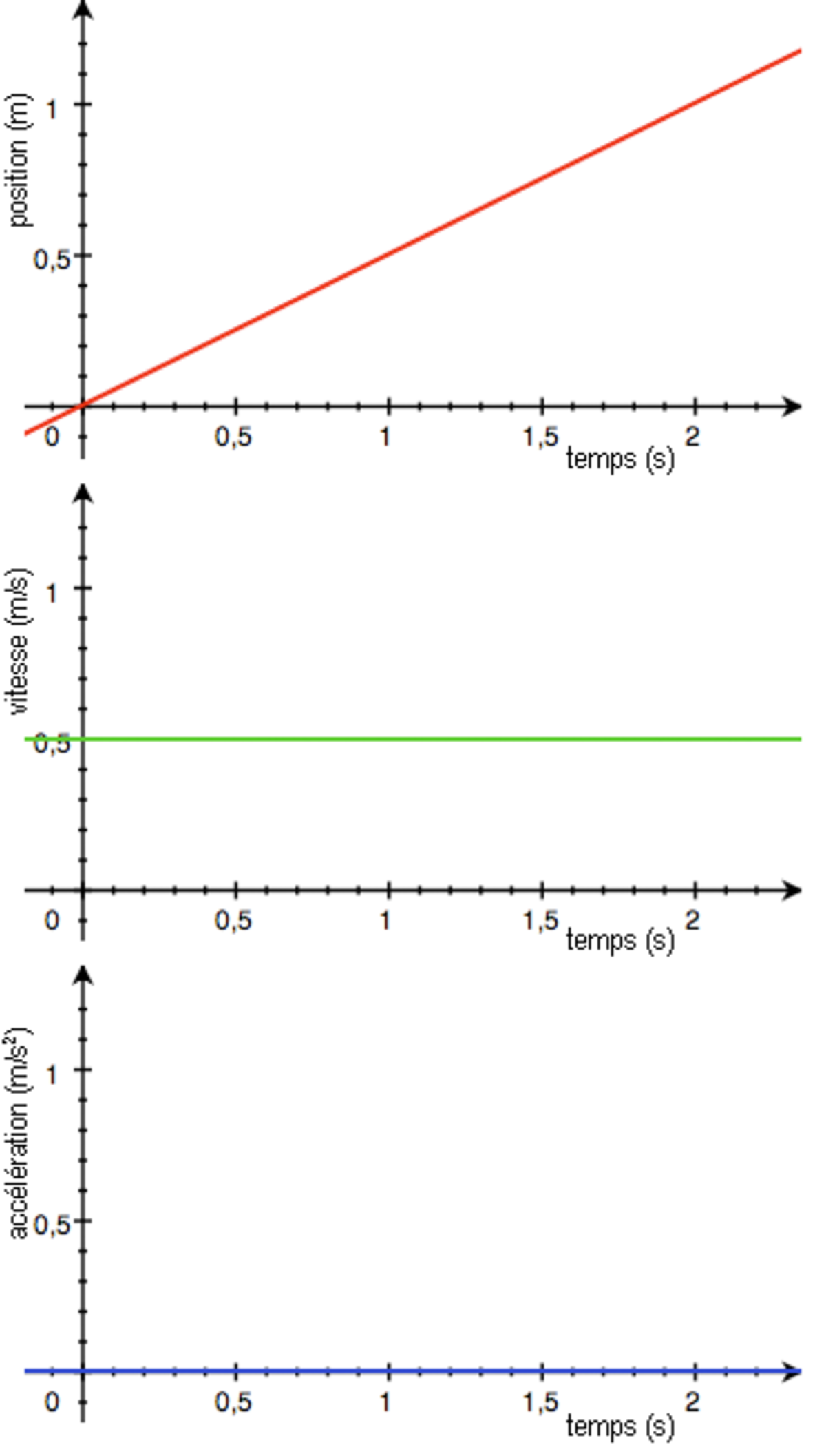
Le cas le plus simple est celui du mouvement rectiligne : la trajectoire décrite est une droite.

Mouvement rectiligne uniforme (MRU)

Le mouvement est dit rectiligne uniforme si la vitesse v est constante ; cela correspond au mouvement d'un objet lancé dans l'espace hors de toute interaction, ou encore au mouvement d'un objet glissant sans frottement. On a :

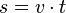
L'abscisse curviligne est alors une fonction linéaire du temps.

Mouvement dans lequel tout segment reliant 2 points du solide reste parallèle à lui-même au cours du temps est aussi une définition classique du mouvement rectiligne uniforme.

En étude des vitesses, ce type de mouvement a une propriété fondamentale. Tous les points d'un solide en translation rectiligne uniforme ont le même vecteur vitesse.

On considère de plus qu'un solide immobile est en translation rectiligne uniforme : L'immobilité est un cas particulier du mouvement rectiligne uniforme.

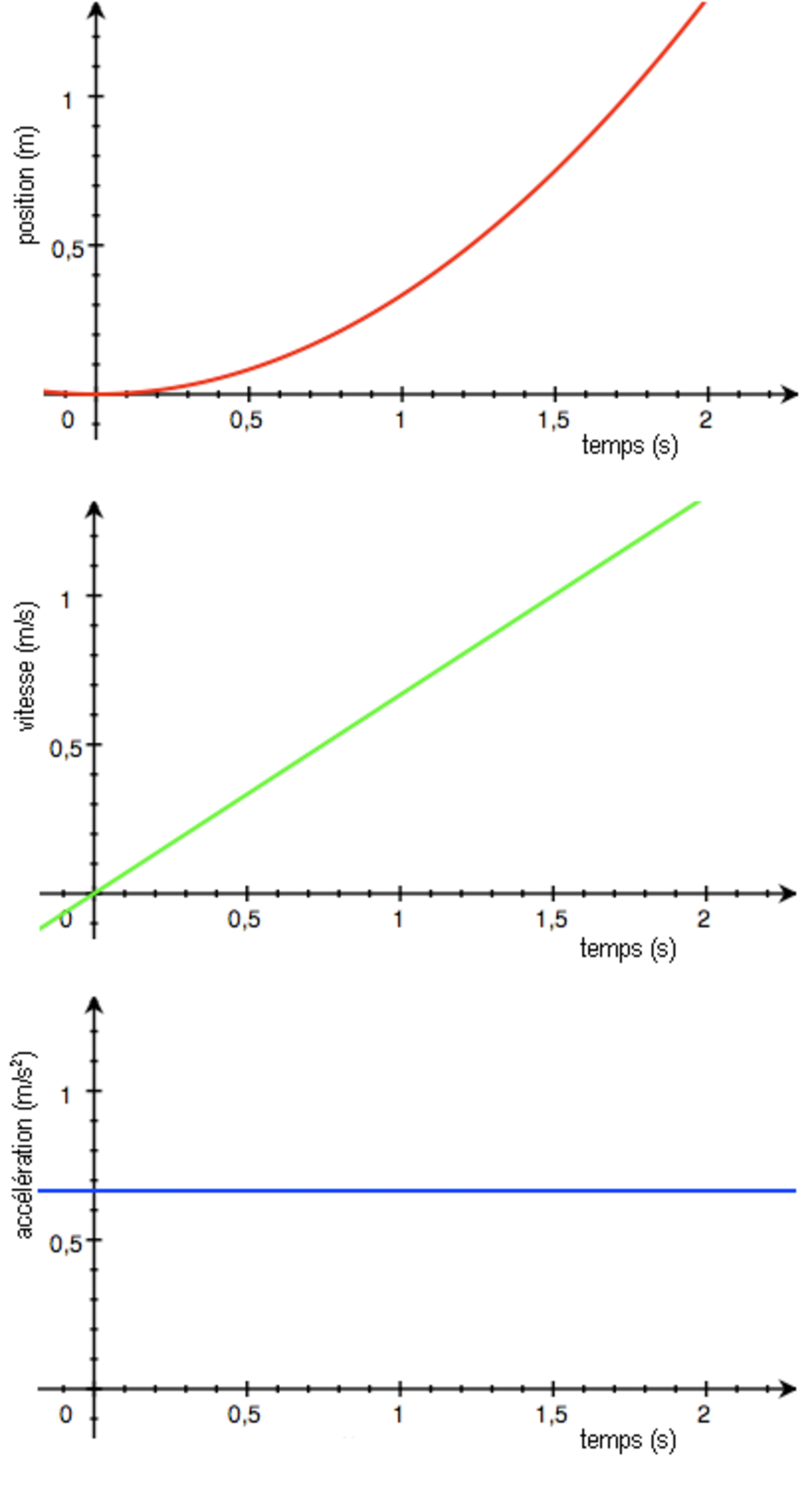
Mouvement rectiligne uniformément accéléré (MRUA)

Evolution de la position, de la vitesse et de l'accélération d'un corps dans un mouvement rectiligne uniformément accéléré.

Le mouvement peut être rectiligne uniformément accéléré — MRUA — (on dit aussi rectiligne uniformément varié) ; le vecteur accélération est constant. Ceci correspond à la chute libre (sans frottement) d'un objet lâché avec une vitesse initiale nulle ou dirigée verticalement ; ou bien un mouvement sans frottement sur un plan incliné d'un mobile lâché avec une vitesse initiale nulle ou dirigée par la pente du plan incliné. On a l'accélération

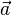
qui est constante, soit :

où v₀ est la vitesse à t = 0 (elle est nulle si l'objet est lâché sans vitesse initiale), et

(on prend x₀ = 0 à t = 0). La vitesse est une fonction linéaire du temps, et l'abscisse curviligne est une fonction parabolique du temps.

Dans le cas de la chute d'un corps, a = − g, où g est l'accélération de la pesanteur au lieu considéré.

Le temps nécessaire au solide pour atteindre une position, se calcule en fonction de l'accélération et en fonction des conditions initiales.

Exemple

Prenons une fusée dont la position x varie à chaque instant t ; elle suit une trajectoire rectiligne A–B. Elle subit une accélération a de 6 m·s^-2, et on prend x = 0 et v = 0 à t = 0.

Si sa vitesse était constante, on aurait

x= v·t.

Mais comme la fusée a une accélération continue, il faut utiliser

x = 1/2·a·t ².

Donc, après 5 secondes de vol depuis A, la fusée est à (6/2)·(5²) = 75 mètres de A. Maintenant pour connaître sa vitesse, on calcule

v = a·t.

Donc si la fusée est en vol depuis 5 secondes, sa vitesse est de 30 m·s^-1.

Mouvement circulaire

Le centre d'inertie du mobile décrit un cercle. Cela peut être un mobile contraint à suivre cette trajectoire comme par exemple une bille dans une gouttière circulaire, un pendule à fil dont le fil reste tendu, ou un train sur un rail circulaire.

Le mouvement est dit circulaire uniforme si la norme de la vitesse est constante. L'équation horaire est alors du type

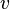
où (x_C, y_C) sont les coordonnées du centre du cercle, r est le rayon du cercle et ω est la vitesse angulaire du centre d'inertie du mobile, exprimée en radian par seconde. On a :

Le vecteur vitesse est tangent au cercle ; on a :

On voit aussi que l'accélération est toujours dirigée vers le centre du cercle (on parle d’accélération centrale centripète), et sa norme vaut

Ceci explique que lorsque l'on tourne en voiture, plus le virage est serré (r est faible), plus l'accélération est importante.

mouvement circulaire uniforme : la vitesse est tangentielle et l'accélération est centripète — l'accélération et la vitesse n'étant pas homogènes, on utilise une échelle différente pour ces deux types de vecteur

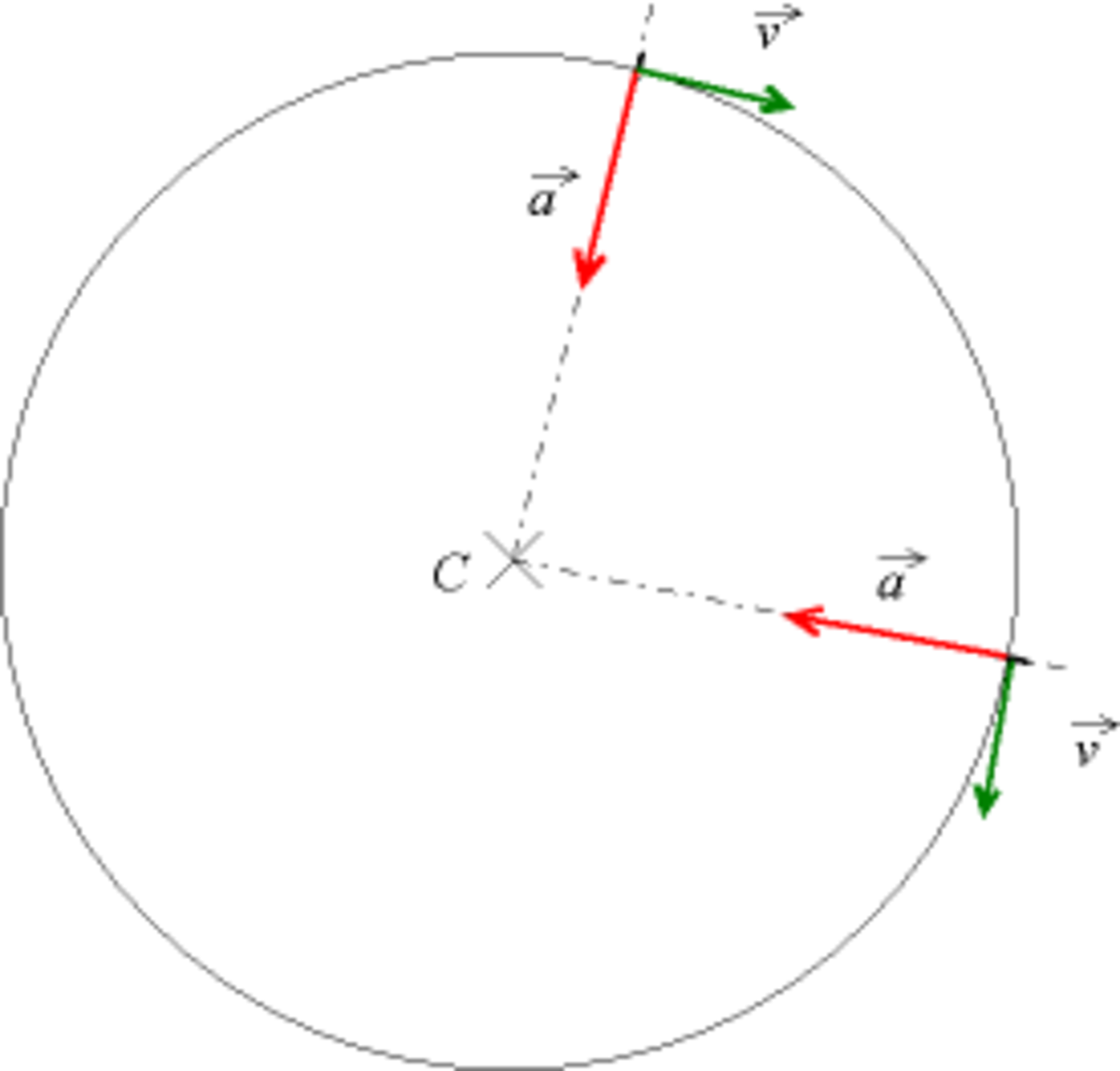
Dans le repère de Frenet, on a :

Le mouvement du pendule à fil ou d'une bille dans une gouttière est circulaire mais pas uniforme.

Mouvement elliptique

Le centre d'inertie du mobile décrit une ellipse (le mouvement circulaire est un cas particulier du mouvement elliptique). Cela peut être le mouvement d'une voiture sur une courbe suivant un arc d'ellipse, ou bien celui d'un satellite autour d'une planète dans un référentiel galiléen dans lequel la planète est fixe, ou encore le mouvement d'une planète ou d'une comète autour d'une étoile ; l'objet le plus massif est alors à un des foyers de l'ellipse.

On définit la vitesse aréolaire comme étant l'aire balayée par un rayon joignant le foyer au centre d'inertie du mobile.

Dans le cas des mouvement orbitaux, le moment cinétique par rapport à un foyer ƒ est constant (ceci peut se déduire du principe de conservation du moment cinétique d'un système isolé) :

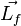
où

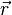
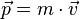
• est le vecteur reliant le foyer au mobile ;
• est la quantité de mouvement du mobile (m est la masse, le vecteur vitesse)
• désigne le produit vectoriel.