Cristal photonique - Définition

Théorie

La présence de bandes interdites peut être prédite par la théorie. Les bandes interdites peuvent être trouvées en calculant le diagramme de dispersion des cristaux. Plus le nombre de dimensions est grand, plus les calculs sont complexes.

Cas d’un cristal photonique à une dimension

Équations de Maxwell

L’existence d’une bande interdite peut être déterminée par le calcul. Il existe plusieurs variantes à la méthode utilisée, mais il est possible d’en définir les étapes les plus importantes. Pour prédire le comportement de propagation des ondes électromagnétiques, les équations de Maxwell sont utilisées. De plus, les phénomènes qui se produisent, en incluant la propagation de la lumière dans un cristal photonique, appartiennent à l’électromagnétisme macroscopique. Et en assimilant les matériaux à des milieux continus, avec des propriétés telles que l’indice de réfraction, la permittivité, la conductivité, et/ou différentes susceptibilités, l’utilisation des équations de Maxwell dans la théorie macroscopique est préférée.

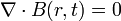
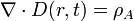
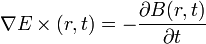
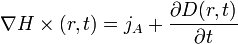
Diverses considérations sont ensuite faites sur les propriétés des matériaux, dont notamment :

• La limitation à un milieu diélectrique, c’est-à-dire qui ne possède que des régions diélectriques homogènes, avec une structure qui ne varie pas avec le temps et libre de charges.
• Le matériau est isotrope, linéaire et non dispersif.
• La perméabilité magnétique μ(r) étant très proche de l’unité pour la plupart des matériaux concernés, il est possible d’écrire B = μ₀H.
• L’absence de sources de lumières dans la structure, c'est-à-dire ρ_A = 0, j_A = 0

Les vecteurs de champ électrique et magnétique sont décrits en nombres complexes, sous la forme d’ondes planes :

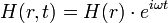
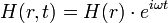
Ce qui permet d’obtenir après plusieurs arrangements combinaisons et simplifications :

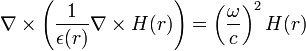
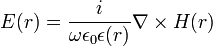
La première équation est l’équation maîtresse pour l’étude de diagrammes de dispersion. La deuxième permet de retrouver le vecteur champ électrique. Les deux premières équations de Maxwell n’apparaissent plus car elles sont facilement vérifiées : avec une onde plane , il suffit d’avoir un vecteur d’onde k qui satisfasse  ; et de même pour le champ électrique. À partir d’ici, la résolution pour une structure ε_r(r) se fait en résolvant l’équation maîtresse pour trouver les modes H(r) et leurs fréquences correspondantes, et en utilisant ensuite la deuxième équation qui permet de retrouver E(r). Il est toutefois possible de procéder de la manière inverse, c'est-à-dire trouver E(r) puis H(r), en recombinant les deux dernières équations. L’étape suivante consiste à introduire un opérateur hermitien Θ et à démontrer que (ΘH,H) = (H,ΘH), ce qui permet de déterminer plusieurs propriétés sur les vecteurs propres H(r) :

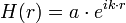
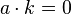
• Les valeurs propres sont réelles.
• Pour deux fréquences ω₁ et ω₂, on doit obtenir (H₁,H₂) = 0, ce qui signifie que les vecteurs propres H(r) sont orthogonaux.
• Les modes concentrent l’énergie des champs électriques dans les zones à forte constante diélectrique. La démonstration est faite avec le théorème variationnel, analogue au principe variationnel en mécanique quantique.
• Simplification des résolutions par des symétries des modes électromagnétiques dans une structure diélectrique.

Théorème de Bloch-Floquet

Le théorème de Bloch-Floquet a été initialement posé pour trouver les solutions de l’équation de Schrödinger indépendante du temps pour un potentiel périodique donné. Il a ensuite été appliqué dans le cas d’un cristal parfait pour décrire la conductivité des électrons, et finalement dans le cas d’un cristal photonique. Le théorème donne la forme des fonctions propres. Pour l’obtenir, des considérations sont faites sur les opérateurs de translations, et la zone de Brillouin est introduite. Ainsi, chaque valeur du vecteur d’onde k dans la zone de Brillouin représente un état propre de Θ ayant une fréquence ω(k)et un vecteur propre H_k de la forme :

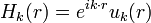
Où u_k(r) est une série périodique de Fourier. Le théorème permet de conclure que les modes électromagnétiques H_k peuvent être écrits comme des états de Bloch.

Résolution

Toutes les informations sur les modes électromagnétiques sont données par le vecteur d’onde k et la fonction périodique u_k(r). En réintroduisant l’équation précédente d’un état de Bloch dans l’équation maîtresse, u_k(r) peut être déterminé. On définit un nouvel opérateur hermitien Θ_k définit par :

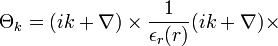
L’équation finale à résoudre est alors:

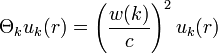
La résolution de cette équation s’effectue alors dans la zone de Brillouin, avec . Les modes d’un cristal photonique peuvent alors être décris comme une famille de fonctions continues, ω_n(k), indexées dans un ordre de fréquence croissante par le numéro de bande n. L’information contenue dans ces fonctions est reportée sur le diagramme de dispersion du cristal photonique. Les solutions sont déterminées par de puissants outils informatiques, avec par exemple la méthode d’accroissement des ondes planes.

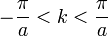
Présence de bandes interdites

Cristal Photonique 1D avec deux indices de réfraction ε_A et ε_B et une période a.

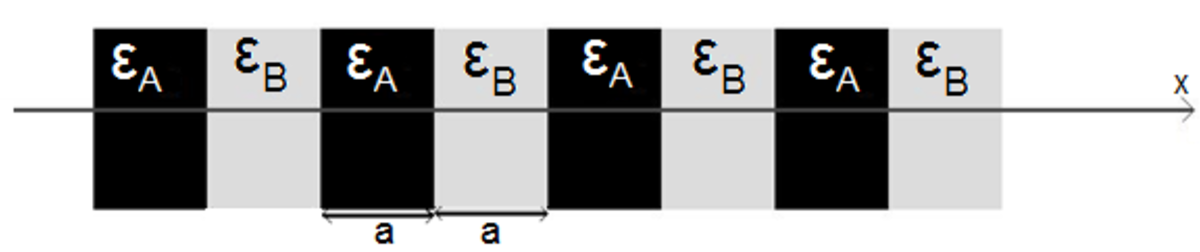
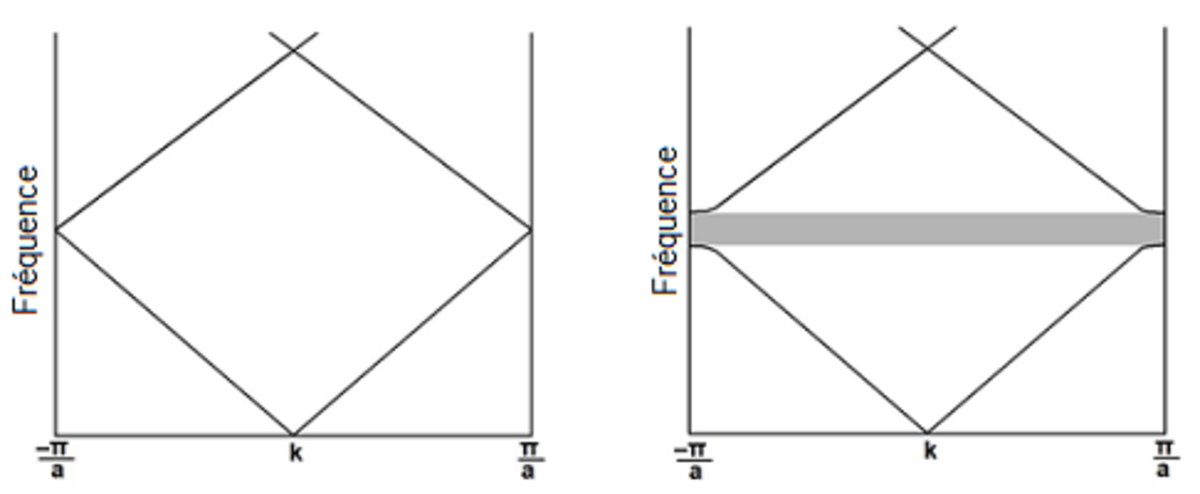
La comparaison de deux structures, l’une avec ε_A = ε_B, et l’autre avec permet d’observer la présence d’une bande interdite :

Diagrammes de dispertion pour un cristal photonique 1D avec ε_A = ε_B à gauche, à droite.

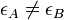
À cause de la périodicité dans la zone de Brillouin, la fréquence à est la même qu’à . Physiquement, l’origine de la bande interdite peut être comprise en considérant le profil électrique pour les états au-dessus et en-dessous de la bande interdite. Il est aussi possible de remarquer que la bande interdite se forme vers . En fait, pour , les modes ont une longueur d’onde de 2a, ce qui signifie que ces modes ne peuvent être centrés que de deux différentes façons dans le cristal : soit dans les couches à haute permittivité électrique ε, soit dans les couches à basse permittivité électrique ε.

Structures de cristal photonique 1D avec ε_A < ε_B. Au-dessus : Champ électrique pour le mode de la bande au-dessus de la bande interdite, centré dans les couches à basse permittivité électrique. En-dessous : Champ électrique pour le mode de la bande au-dessous de la bande interdite, centré dans les couches à haute permittivité électrique.

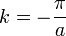
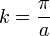
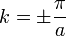
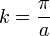
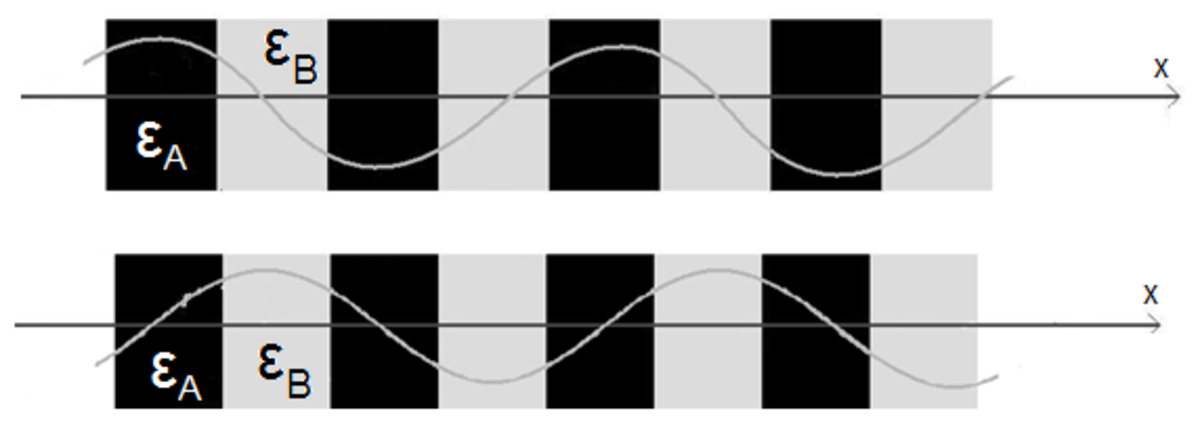
Il y aura donc plus d’énergie pour la bande du dessous à cause des sommets qui se concentrent dans les régions à haute permittivité électrique, et moins pour la bande du dessus. De cela résulte la différence de fréquence entre les deux cas.

Méthodes de calcul de diagrammes de dispersion

Pour fabriquer un cristal photonique, il est essentiel de définir au préalable les fréquences et la taille de la bande interdite. Pour cela, plusieurs méthodes de calcul informatisées sont utilisées :

1. La méthode d’accroissement des ondes planes (« Plane wave method » en anglais).
2. La méthode des différences finies pour l’espace et le temps (« Finite Difference Time Domain » en anglais)
3. La méthode spectrale d’ordre N.
4. La méthode d’approximation du « moule à madeleines » (« Muffin-tin approximation » en anglais).

Ces méthodes résolvent principalement les fréquences des cristaux photoniques pour chaque valeur de la direction de propagation donnée par le vecteur d’onde k, ou vice-versa.