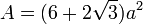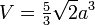Cuboctaèdre - Définition
Source: Wikipédia sous licence CC-BY-SA 3.0.
La liste des auteurs de cet article est disponible ici.
La liste des auteurs de cet article est disponible ici.
Aire et volume
L'aire A et le volume V d'un cuboctaèdre de côté a sont donnés par
Coordonnées cartésiennes
Les coordonnées cartésiennes des sommets d'un cuboctaèdre (de longueur d'arête √2) centré à l'origine sont
- (±1,±1,0)
- (±1,0,±1)
- (0,±1,±1)
| Solides géométriques | ||||
| Les polyèdres | ||||
| Les solides de Platon | ||||
| Tétraèdre régulier - Cube - Octaèdre régulier - Icosaèdre régulier - Dodécaèdre régulier | ||||
| Les solides d'Archimède | ||||
| Tétraèdre tronqué - Cube tronqué - Octaèdre tronqué - Dodécaèdre tronqué - Icosaèdre tronqué - Cuboctaèdre - Cube adouci - Icosidodécaèdre - Dodécaèdre adouci - Petit rhombicuboctaèdre - Grand rhombicuboctaèdre - Petit rhombicosidodécaèdre - Grand rhombicosidodécaèdre | ||||
| Les solides de Kepler-Poinsot | ||||
| Petit dodécaèdre étoilé - Grand dodécaèdre étoilé - Grand dodécaèdre - Grand icosaèdre | ||||
| Les solides de Catalan | ||||
| Triakioctaèdre - Tétrakihexaèdre - Triakitétraèdre - Pentakidodécaèdre - Triaki-icosaèdre - Dodécaèdre rhombique - Icositétraèdre pentagonal - Triacontaèdre rhombique - Hexacontaèdre pentagonal - Icositétraèdre trapézoïdal - Hexakioctaèdre - Hexacontaèdre trapézoïdal - Hexaki icosaèdre | ||||
| Les solides de Johnson | ||||
| Les solides de révolution | ||||
| Boule - Cylindre de révolution - Cône de révolution - Tore - Paraboloïde de révolution |