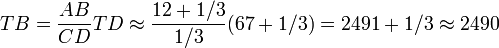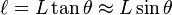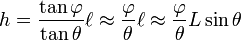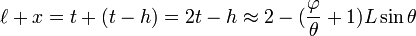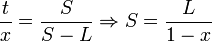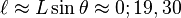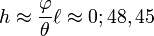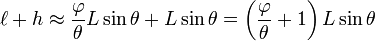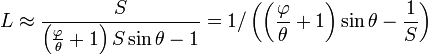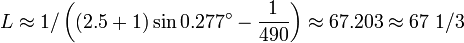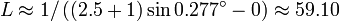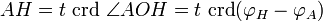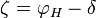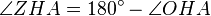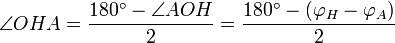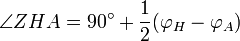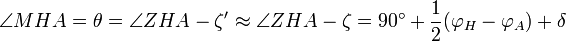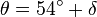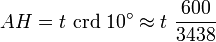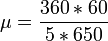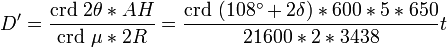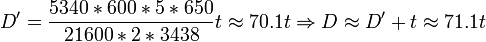Des grandeurs et des distances du Soleil et de la Lune - Définition

Conclusions

Si ces reconstitutions reflètent réellement le contenu des Grandeurs et distances, on ne peut que trouver ce travail remarquable. C'est tout au moins l'avis de Toomer:

Ce procédé, si je l'ai construit correctement, est tout à fait remarquable (...) Ce qui est étonnant, c'est la sophistication dans l'approche du problème par deux méthodes différentes et aussi la totale honnêteté avec laquelle Hipparque révèle ses résultats discordants (...) qui appartiennent néanmoins au même ordre de grandeur et, pour la première fois dans l'histoire de l'astronomie, constituent une bonne approximation.

En tout état de cause, en effet, même si Ptolémée et Pappus font quelque peu la fine bouche, les résultats obtenus par Hipparque pour la distance Terre-Lune sont remarquablement proches de la réalité, puisque la distance moyenne de la lune est en réalité d'approximativement 60,2 rayons terrestres équatoriaux. Comme l'évaluation du dit rayon terrestre était meilleure chez Ératosthène (et donc chez Hipparque) que chez Ptolémée, ce dernier était, au final, plus éloigné de la réalité. Il est intéressant de remarquer que si l'on applique le procédé du livre II avec les valeurs présentes chez Théon de Smyne et chez Cléomède, on aboutit respectivement à 60,5 et 61 rayons terrestres.

Pour la distance Terre-Soleil, à l'inverse, Hipparque était loin du compte, puisque la distance moyenne est d'environ 23 455 rayons terrestres : avec des triangles aussi étirés, la moindre différence d'angle entraîne des écarts considérables pour la distance.

Cette approche, qui consiste à déterminer les limites d'une quantité inconnue n'était pas neuve : Aristarque de Samos fit de même, tout comme Archimède pour le nombre pi. Mais dans ce cas, les limites reflétaient une incapacité de déterminer une constante mathématique et non une incertitude dans l'observation.

Reconstitutions modernes

Trois tentatives de reconstitutions ont été recensées et analysées par Neugebauer :

Hultsch

La première tentative fut réalisée par Friedrich Hultsch en 1900, mais elle fut réfutée en 1969 par Noel Swerdlow et par G. J. Toomer en 1974.

Friedrich Hultsch estimait que la source de Pappus comportait une erreur de copie et que la distance du soleil calculée par Hipparque devait être 2490 et non 490 rayons terrestres. En numération grecque, un seul caractère muni d'un signe diacritique différencie ces deux nombres. Son analyse reposait sur un texte de Théon de Smyrne qui indique qu'Hipparque avait trouvé que la grandeur du soleil valait 1880 fois celle de la terre, et que la grandeur de la terre valait 27 fois celle de la lune.

En supposant que Théon parlait de volumes, il obtient un rayon solaire (AB) égal à 12+1/3 rayons terrestres et un rayon lunaire (CD) égal à 1/3 de rayon terrestre.

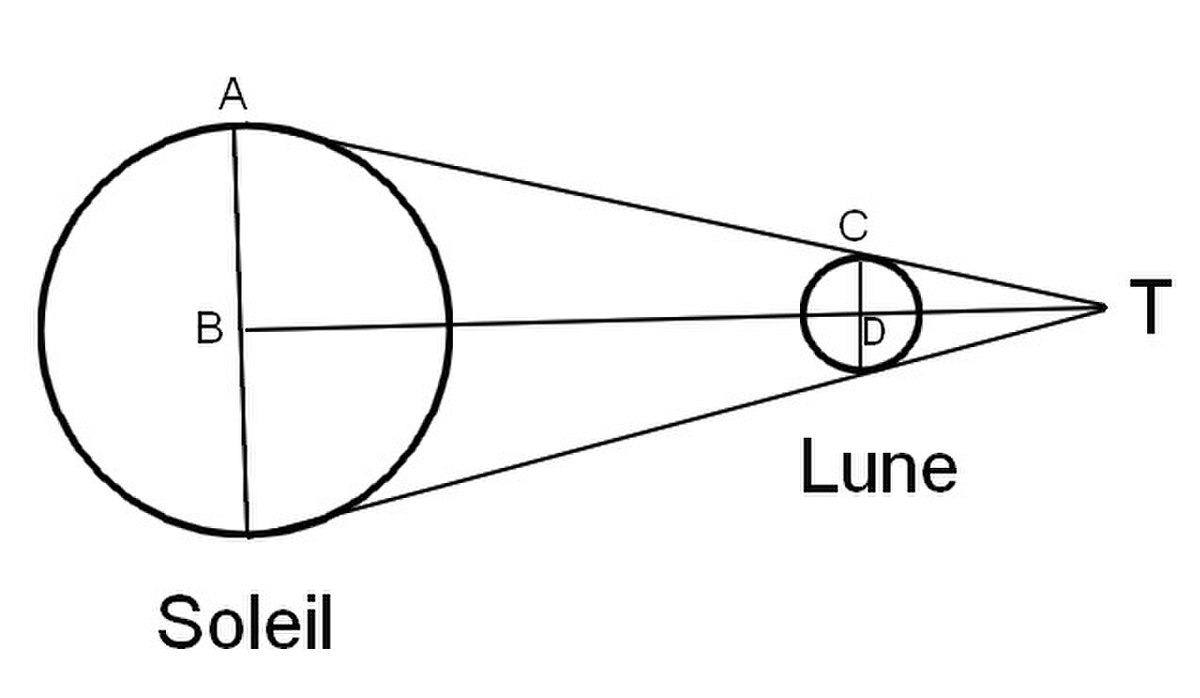
Considérant que l'observateur terrestre (T) voit le Soleil de la même grandeur que la Lune (figure 1), les triangles ABT et CDT sont semblables et leurs côtés sont proportionnels. Si l'on suppose, avec Hipparque, que la distance Terre-Lune (TD) vaut 67+1/3 (rayons terrestres), on a :

Swerdlow : reconstitution d'après le livre II

Swerdlow considère qu'Hipparque calcule les distances du Soleil et de la Lune en utilisant une construction présente dans Ptolémée. Il n'est pas absurde, en effet, de penser que ce calcul fut initialement développé par Hipparque, qui fut une source primaire de l'Almageste.

En effectuant le calcul qui suit, Swerdlow put aboutir au résultats d'Hipparque (67 1/3 pour la Lune et 490 pour le Soleil), en utilisant certaines approximations bien précises.

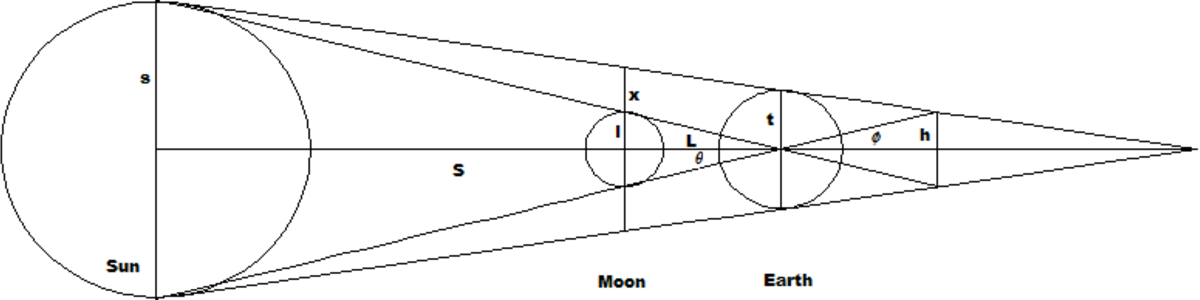
Si l est le rayon lunaire et L la distance Terre-Lune par rapport aux centres de ces astres ; si s et S sont les valeurs correspondantes pour le Soleil, la trigonométrie donne :

et

En traçant x et h parallèles équidistantes à t, on obtient :

et par les triangles semblables :

La combinaison de ces équations donne :

Les valeurs adoptées par Hipparque pour θ, ϕ et L se trouvent dans l'Almageste et dans Pappus. Ptolémée dit qu'Hipparque a trouvé que l'orbite de la lune mesure 650 fois son cercle et que le diamètre angulaire de l'ombre de la terre est 2,5 fois celui de la lune. D'autre part, Pappus nous informe que la valeur retenue en définitive par Hipparque comme distance moyenne de la Lune est de 67 1/3 rayons terrestres.

En d'autres termes,

• θ, le diamètre angulaire apparent de la Lune vaut 360°/650 = 0,554°
• ϕ, le diamètre angulaire apparent de l'ombre de la terre au niveau de l'orbite lunaire, vaut 2.5 X θ = 1,385°
• L, la distance Terre-Lune vaut 67 1/3 rayons terrestres.

Selon Swerdlow, Hipparque calcule l'expression ci-dessus en arrondissant les résultats comme suit (en sexagésimal) :

et

Puis, étant donné que

il s'ensuit que

\ell \approx L \sin \theta \approx 0;19,30

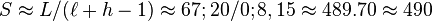
Swerdlow utilise ce résultat pour montrer que 490 était la leçon correcte du texte de Pappus, invalidant ainsi l'interprétation de Hultsch. Toutefois, ce résultat est très dépendant des approximations et arrondissements utilisés. Néanmoins, son raisonnement a été largement accepté, bien qu'il restât aussi la question de avoir d'où Hipparque tire la distance lunaire de 67 1/3.

Conformément à Pappus et Ptolémée, Swerdlow suggère qu'Hipparque considérait les 490 rayons terrestres comme la distance minimale possible de la Terre au Soleil. Cette distance correspond à une parallaxe solaire de 7', qu'il pensait être le plus grand angle qui soit indiscernable. En fait, la résolution normale de l'oeil humain est de 2'.

La formule utilisée plus haut peut, bien entendu être inversée pour obtenir la distance lunaire à partir de la distance solaire :

Soit, avec les valeurs définies plus haut :

Toomer prolonge le raisonnement en observant que si la distance solaire croît considérablement, la valeur de -1/S tend vers zéro et la distance lunaire s'approche de sa valeur moyenne minimale :

ce qui est proche de la valeur retenue ultérieurement par Ptolémée.

Toomer : reconstitution d'après le livre I

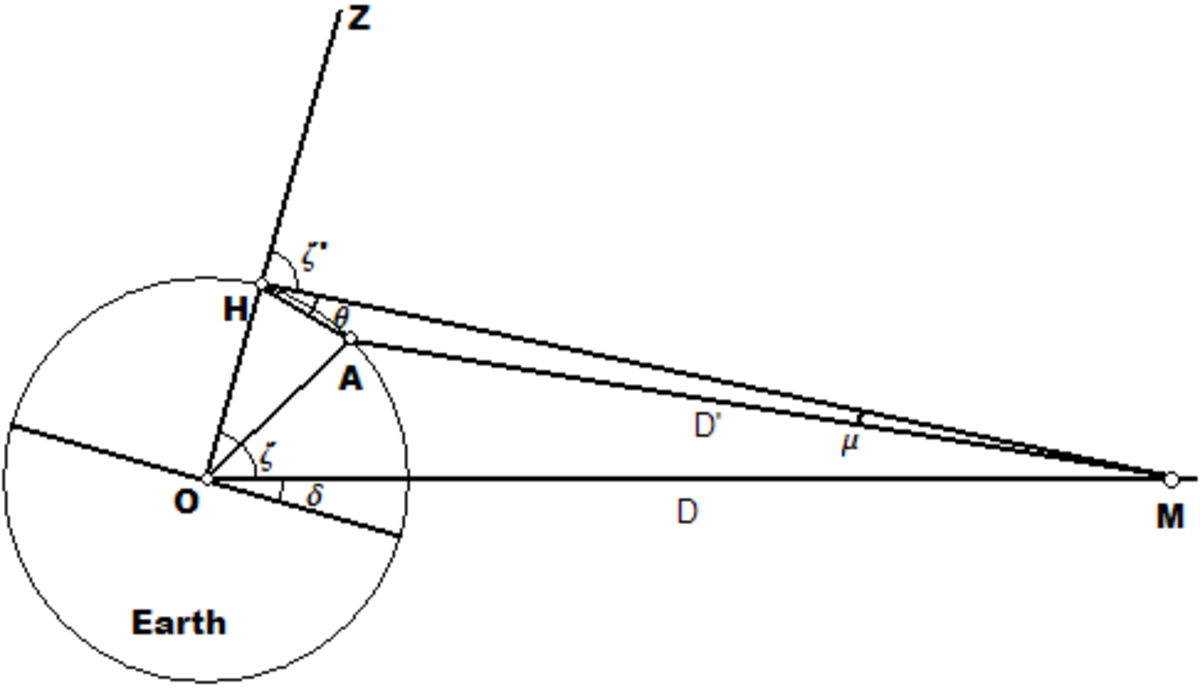
En plus de l'explication de la distance lunaire minimale telle que la trouva Hipparque, Toomer parvint à décrire la méthode du premier livre, qui utilise une éclipse solaire. Pappus indique que l'éclipse fut totale dans la région de l'Hellespont, mais fut observée au 4/5 de la totalité à Alexandrie.

Si Hipparque suppose que le Soleil est infiniment distant (cf Pappus : " La terre a la proportion d'un point au centre (de l'orbite) du Soleil), alors la différence dans la magnitude de l'éclipse doit être due exclusivement à la parallaxe et, par suite, à la distance de la lune. En se basant sur des données issues de l'observation, il devrait pouvoir déterminer cette parallaxe et dès lors la distance de la lune. Hipparque devait connaître et , les latitudes d' Alexandrie et de l'Hellespont, respectivement. Il devait aussi connaître δ, la déclinaison de la Lune au moment de l'éclipse, et μ, qui représente la différence de magnitude de l'éclipse entre les deux régions.

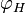
Soit t le rayon terrestre et crd la fonction corde, définie par la table des cordes d'Hipparque.

Comme la lune est très lointaine, on peut admettre l'approximation . De cette manière , on a :

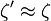
Donc,

Connaissant AH et θ, la valeur de µ suffit pour obtenir D'. Puisque l'éclipse était totale en H et au 4/5 de la totalité en A, µ vaut 1/5 du diamètre apparent du Soleil. Cette valeur était bien connue d'Hipparque, qui lui attribuait 1/650 de cercle. La distance entre les centres de la Lune et de la Terre résultera donc de .

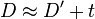
Toomer a déterminé comment Hipparque obtint la corde des petits angles. Les valeurs qu'il attribue pour les latitudes de l'Hellespont (41 degrés) and Alexandrie (31 degrés) sont connues par la Géographie de Strabon. Quant à la déclinaison, il faut savoir, pour la déterminer, de quelle éclipse Hipparque fit usage.

Sachant qu'Hipparque attribuait à la distance Terre-Lune une valeur proche de 71 rayons terrestres et connaissant la région où se produisit l'éclipse, Toomer détermina qu'il s'agissait de l'éclipse du 14 mars 190 av. J.-C., qui concorde en outre avec les données historiques dont on dispose. Cette éclipse fut totale à Nicée, lieu de naissance probable d'Hipparque. Elle est également mentionnée par Strabon. La déclinaison de la lune à ce moment était de : Par la trigonométrie des cordes, on a :

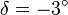
et en utilisant la table des cordes d'Hipparque, on obtient :

donc

Ce qui concorde avec les 71 rayons terrestres rapportés par Pappus.