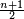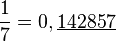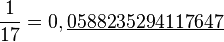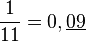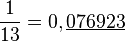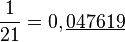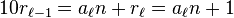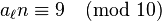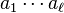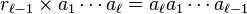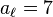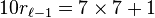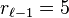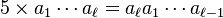Développement décimal périodique - Définition

Période de 1/n

La connaissance d'une période pour le développement décimal de 1/n permet d'en découvrir par multiplication pour tout quotient m/n. Le développement de 1/n possède plusieurs périodes (il suffit pour en créer une nouvelle de mettre bout à bout deux périodes identiques), l'intérêt est de travailler sur la plus courte que l'on appellera la période et d'en déterminer certaines propriétés.

Longueur de la période

Les exemples précédents ont mis en évidence le rôle de la répartition des restes dans la division a par b , c'est-à-dire dans le cas présent , les restes dans la division de 1 par n. Ces restes correspondent aux restes de 10^k dans la division euclidienne par n. Cette question se traite bien si l'on fait intervenir l'arithmétique modulaire et les notions de congruence sur les entiers et plus précisément l'ordre de 10 dans muni de la multiplication. L'ordre de 10 est le plus petit entier ℓ tel que 10 ^ℓ -1 soit multiple de n. L'arithmétique modulaire démontre que, si 10 et n sont premiers entre eux, cet ordre est toujours un diviseur de φ(n) où φ est la fonction d'Euler, φ(n) représente le nombre d'entier compris entre 1 et n - 1 et premiers avec n

On peut démontrer les résultats suivants :

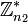
Lorsque n est un nombre premier différent de 2 et 5, la période de 1/n peut être de n - 1. C'est la période maximale pour une division par n. Ce cas se produit par exemple pour 1/7 et 1/17

mais elle peut aussi être plus courte comme dans le cas de 1/11 ou 1/13

Mais elle reste toujours un diviseur de n - 1.

Les périodes de longueur maximal sont donc celle des fractions 1/n où n est un nombre premier pour lequel l'ordre de 10 est n - 1. On dit alors que 10 est une racine primitive modulo n. Emil Artin s'est intéressé à ce type de nombre premier. Il a émis l'hypothèse qu'il existe une infinité de nombres premiers de cette sorte et que leur densité parmi les nombres premiers est une constante valant environ 0,374.

Lorsque n n'est pas premier, φ(n) < n - 1. La longueur de la période doit diviser φ(n) et elle n'est jamais maximale. Ainsi la période de 1/21 doit diviser φ(21) = 2 × 6 = 12. En effet la période de 1/21 est de longueur 6

Cycle et permutation

Si n et 10 sont premiers entre eux, la division posée pour 1/n permet de trouver aussi les développement décimaux de r_k/n pour tout les restes intervenant dans la division. En effet, r_k a pour quotient a_{k + 1} et pour reste r_k+1 dans la division par n. On retrouve alors pour le développement périodique de r_k/n, celui de 1/n ayant seulement subi une permutation circulaire et commençant à a_k+1. Ainsi on a

,

,

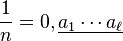
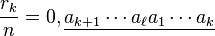
et l'écriture fractionnaire donne

,

.

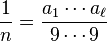
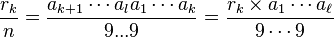
En observant les numérateurs, on peut voir que multiplier la période de 1/n par r_k équivaut à effectuer une permutation circulaire sur les chiffres de ce nombre

Lorsque la période de 1/n est de longueur maximale, les restes parcourent tous les entiers de 1 à n - 1. Dans ce cas, on peut multiplier la période de 1/n par tout entier m < n, on conservera toujours les mêmes chiffres à une permutation près. La nouvelle période obtenue sera celle de m/n.

Cette propriété rend remarquables les périodes des nombres 1/n pour lesquels 10 est d'ordre n - 1. C'est le cas par exemple de 142857 période de 1/7 ou 052631578947368421 période de 1/19 qui sont des nombres cycliques. On a ainsi :

• 1 × 142857 = 142857
• 2 × 142857 = 285714
• 3 × 142857 = 428571
• 4 × 142857 = 571428
• 5 × 142857 = 714285
• 6 × 142857 = 857142
• 7 × 142857 = 999999 (période de l'écriture décimale impropre de 1.

Lorsque la période de 1/n n'est pas de longueur maximale, seuls ℓ entiers sont concernés, chacun associé à une permutation circulaire de la période de 1/n. Si l'entier m, premier avec n ne fait pas partie de ce premier groupe, la période de m/n est alors m *a₁...a _ℓ = b₁...b _ℓ différente de la précédente. A chaque permutation de cette nouvelle période est associée un autre quotient de la forme m'/n .On répartit ainsi tous les entiers premiers avec n dans des ensembles disjoints contenant ℓ éléments et associés à φ(n)/ℓ périodes différentes.

Pour n=27 par exemple, on a φ(27)=2 × 9 = 18 et 1/27 a pour période 037. Cette période engendre 5 autres périodes qui sont les seules périodes possibles à une permutation circulaire près de tout quotient m/27 où m et 27 sont premiers entre eux.

• 037 pour m=1, 370 pour m=10, 703 pour m=19
• 074 pour m=2, 407 pour m=11, 740 pour m=20
• 148 pour m=4, 481 pour m=13, 814 pour m=22
• 185 pour m=5, 518 pour m=14, 851 pour m=23
• 259 pour m=7, 592 pour m=16, 925 pour m=25
• 296 pour m=8, 629 pour m=17, 962 pour m=26

Construction

Si n est premier avec 10, on peut construire la période de 1/n en posant la division mais on peut aussi la reconstituer uniquement par multiplication à partir de son dernier terme.

L'égalité

permet de dire que

ou, plus simplement, que ce produit doit se terminer par 9.

Comme n est premier avec 10, un tel nombre a_ℓ existe, il n'en existe d'autre part qu'un seul compris entre 1 et 9. On peut le trouver en résolvant l'équation diophantienne nx - 10y = 9. Le nombre a_ℓ étant trouvé, on en déduit la valeur de r_ℓ-1.

D'autre part, si on note

la période recherchée, on sait, par permutation circulaire que

Ce produit permet de déterminer a_{ℓ -1} qui, réinjecté dans la même égalité permet de trouver a_{ℓ -2} et de proche en proche permet de découvrir tous les chiffres de la période.

Par exemple, pour déterminer la période de 1/7, on cherche d'abord le chiffre qui multiplié par 7 donne un nombre se terminant par 9. Puisque 7 × 7 = 49, on peut poser

puis, comme

on sait que

Les chiffres successifs de la période se trouvent en remplissant progressivement la multiplication à trous

. . . . . 7 × 5 .3 5

. . . . 5 7 × 5 . 2 8 5

. . . 8 5 7 × 5 . 4 2 8 5

. . 2 8 5 7 × 5 . 1 4 2 8 5

. 4 2 8 5 7 × 5 . 2 1 4 2 8 5

1 4 2 8 5 7 × 5 7 1 4 2 8 5

C'est ce principe qui est utilisé dans la construction de la période de 1/19 dont le dernier terme est 1 et dont l'avant dernier reste est 2.

Structure

On se place ici dans le cas où n est premier, supérieur ou égal à 7 et on suppose que la période la plus courte de 1/n est de longueur ℓ =st où s>1. La période est alors constituée de s blocs de t chiffres. Si on note A₁, ... A_s ces blocs, ils peuvent être vus comme l'écriture décimale de s nombres. La somme de ces s nombres est alors toujours un multiple de 10^t - 1 = 99...9. De plus, on peut démontrer que, si le nombre de blocs n'est que de 2 ou 3, la somme est exactement égale à 10^t - 1.

Par exemple, la période de 1/7 est de 142857, partageable en 6, 3, ou 2 blocs

• en deux blocs :142+857 = 999
• en 3 blocs : 14+28+57 = 99
• en 6 blocs : 1+ 4 + 2 + 8 + 5 + 7 = 36 (divisible par 9)

Cette propriété porte le nom de théorème de Midy.

O. Mathieu a démontré que si n est premier supérieur ou égal à 13, la décimale de rang est selon le reste de n modulo 40, tantôt 0 tantôt 9.