Développement décimal périodique - Définition

Notations

Il est possible de noter la répétition de chiffres à l'infini en plaçant des points de suspension après plusieurs occurrences de décimales. Cette écriture peut paraître claire lorsqu'une seule décimale est répétée une dizaine de fois, mais d'autres notations sont plus explicites en décomposant le nombre rationnel en trois parties :

• sa partie entière,
• une partie décimale non périodique,
• une partie décimale périodique.

Les chiffres de la partie entière sont placés classiquement à gauche de la virgule, qui est suivie par les chiffres de la partie décimale non périodique. Ceux-ci sont suivis des chiffres de la partie décimale périodique, marqués par une barre au-dessus ou en dessous, voire par des crochets les encadrant.

Fragments d'histoire

L'écriture décimale des entiers apparaît très tôt dans l'histoire des mathématiques notamment en Orient. L'idée de prolonger les opérations au-delà de l'unité est présente en Chine dès le III^e siècle mais la partie décimale y est présentée sous forme d'une fraction décimale. La présentation d'un nombre décimal avec une partie entière, une virgule et une partie décimale apparaît dans les écrits du mathématicien Ibrahim Uqlidisi au X^e siècle quand il présente le système de numération hindou mais le calcul des nombres sous forme de fractions reste prédominant. Le système décimal arrive en Europe tardivement (vers le X^e siècle) et c'est Simon Stevin qui prône l'écriture décimale des nombres fractionnaires qu'il appelle les rompus. Dans son traité La disme, écrit en 1585, il précise les méthodes de calcul sur les écritures décimales et envisage que celles-ci puissent être illimitées et s'appliquer même à des nombres irrationnels (nombres incommensurables).

Au cours du XVIII^e siècle, les mathématiciens se préoccupent de la période décimale des fractions. Un des premiers à utiliser une notation spécifique pour la période d'un nombre fractionnaire est John Marsh qui signale le début et la fin de la période par un point placé au-dessus du chiffre. H. Clarke préfère l'apostrophe tandis que d'autre utilisent des accents avant et après la période. Tout est fait pour faciliter le calcul des fractions sous forme décimale et, tout comme il existe des tables de logarithmes ou des tables de sinus, existent aussi des tables de périodes. Jean le Rond D'Alembert en publie dans son Encyclopédie méthodique. La révolution française privilégie le système décimal dans les unités de mesure et encourage le calcul sous forme décimale. On trouve ainsi dans Introduction abrégée sur les nouvelles mesures qui doivent être introduites dans toute la République au 1er vendémiaire an 10, avec des tables de rapports et de réductions, par C.H. Haros, une table donnant les périodes des fractions de dénominateurs inférieurs à 50.

Carl Friedrich Gauss (1777-1855) par Christian Albrecht Jensen

Une grande avancée et une formalisation de ces notions sont faites par Gauss dans ses Disquisitiones arithmeticae en 1801. Gauss se préoccupe de déterminer facilement le développement périodique de tout rationnel. Cet objectif le conduit à travailler sur les restes dans la division par n qu'il appelle les résidus. Il définit l'ordre d'un nombre modulo n comme le plus petit entier non nul k tel que a^k ait pour reste 1 modulo n. Il s'intéresse aux racines primitives : celles dont les puissances modulo n permettent de donner tous les entiers inférieurs à n et premier avec n. Une racine primitive a étant choisie, Il définit l'indice d'un nombre b comme l'entier i tel que aⁱ a pour reste b modulo n. Cet indice i s'appelle de nos jours le logarithme discret. Il remarque que, si n est premier ou puissance d'un nombre premier, il existe des racines primitives. Dans le chapitre 6 de son traité, il applique ces connaissances aux fractions. Il remarque que toute fraction peut se décomposer en éléments simples, c'est-à-dire en somme de fractions dont le dénominateur est une puissance de nombre premier. Pour chacun de ces dénominateurs n, il détermine une racine primitive a de Z_n*. Il détermine ensuite l'indice i de 10 dans la base a. Il sait alors que la longueur de la période de 1/n est de φ(n)/i et il en détermine la valeur. Il prouve ensuite que la fraction m/n a aussi une période de même longueur et que cette période est à choisir entre i périodes différentes, à une permutation près. Il démontre ensuite que l'indice de m lui permet de déterminer quelle période il doit choisir ainsi que la permutation à effectuer. Il fournit alors pour chaque entier n, premier ou puissance de nombre premier, des tables donnant les périodes et les indices des tous les nombres premiers inférieurs à n.

On peut illustrer sa démarche sur un exemple : il s'agit de chercher le développement décimal de

.

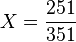
La première étape consiste à décomposer 351 en produit de facteurs premiers :

.

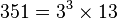
Il faut ensuite décomposer cette fraction en éléments simples. Il faut trouver deux entiers x et y tels que

.

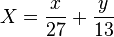
La résolution de l'équation diophantienne 13x+27y=251 donne pour décomposition :

.

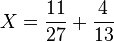
On prend d'abord n=27. La table numérique fournit comme racine primitive 2, l'indice de 10 est de 6, et l'indice de 11 est 13 = 2× 6 + 1. Il existe 6 périodes possibles et celle associée à l'indice 1 est, d'après les tables, 074 donc la période associé 11 est 074 permutée de deux cases 407.

.

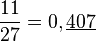
On prend ensuite n=13. la table donne deux périodes, la racine primitive est 6, et 4 est d'indice 10 = 5×2. La période de 4 est la période d'indice 0 (076923) décalée de 5 cases.

.

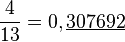
La somme de ces deux nombres a une période de longueur multiple commun des deux longueurs, ici, de longueur 6.

.

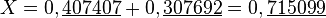
À partir du XIX^e siècle et jusqu'au développement des calculatrices, nombreux sont les ouvrages permettant de calculer à la main les périodes des nombres fractionnaires.