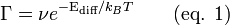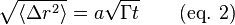Diffusion de surface - Définition

Introduction

Figure 1. Modèle de diffusion d'un adatome sur un réseau de surface carré. La fréquence de vibration de l'adatome est plus grande que la fréquence des sauts aux sites voisins. Ainsi, le modèle montre deux types de sauts : les sauts aux sites voisins les plus proches, et aux prochains voisins les plus proches (en diagonale).

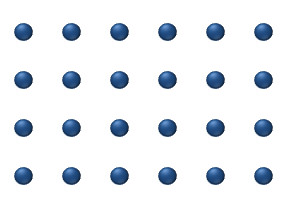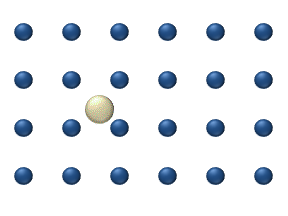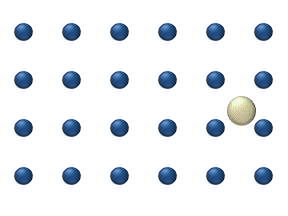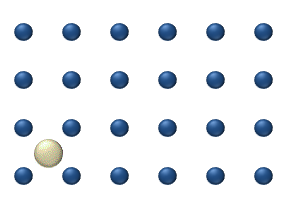
En science des matériaux, la diffusion de surface ou diffusion superficielle est un phénomène impliquant le déplacement d'adatomes, de molécules, et d'agrégats atomiques sur la surface de matériaux solides. Les mécanismes par lesquels cette diffusion s'effectue ont une certaine importance, car ils conditionnent le développement de matériaux ayant des propriétés intéressantes.

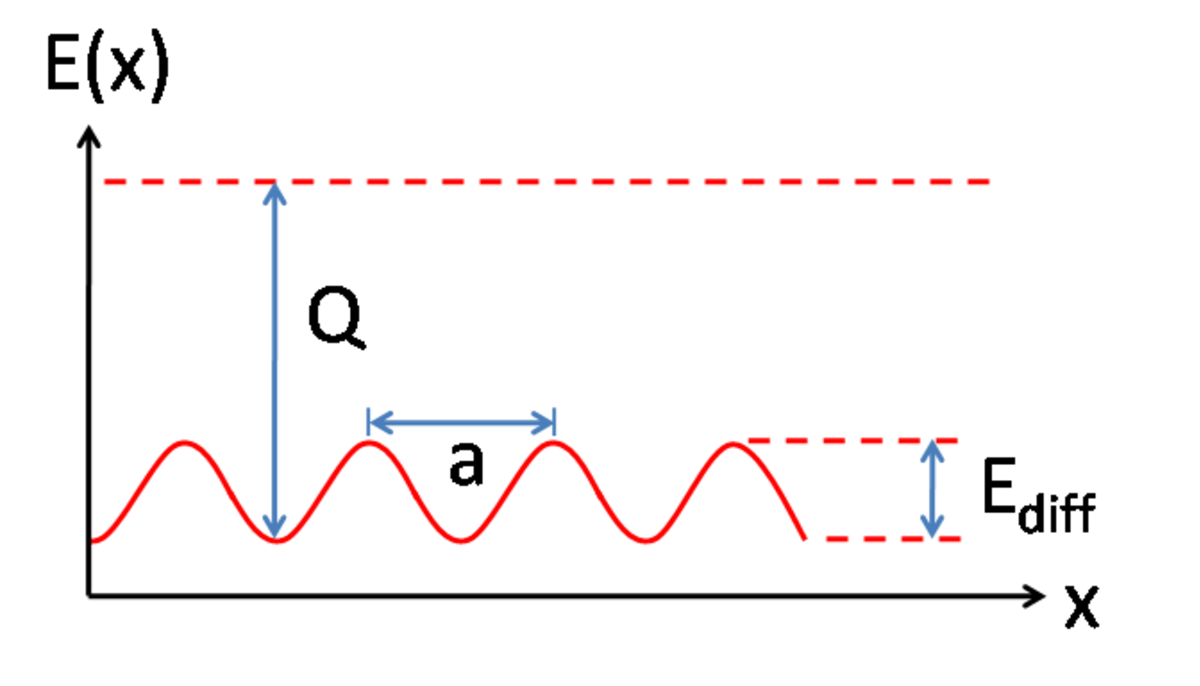
Le processus peut être considéré comme des particules sautant d'un site d'adsorption d'une surface à une autre, comme schématisé sur la figure 1. Comme pour la plupart des diffusions de la matière, ce mouvement est caractéristique d'un processus thermique dont la fréquence augmente avec la température. Il a été mis en évidence que de nombreux systèmes présentent un comportement de diffusion, qui dérive d'un modèle conventionnel de sauts aux voisins proches. La diffusion à effet tunnel est un exemple particulièrement intéressant de mécanisme non conventionnel, dans lequel il a été montré que de l'hydrogène peut diffuser sur une surface métallique via l'effet tunnel.

Plusieurs techniques d'analyse peuvent être utilisées pour étudier les mécanismes de diffusion superficielle, les plus importantes sont la microscopie ionique, la microscopie à effet tunnel. Ce phénomène peut se rencontrer sur de nombreux matériaux, la plupart des expériences sont faites sur des surfaces cristallines. Dû aux contraintes expérimentales, les majorités des études de diffusion de surface sont limitées par la température de fusion du substrat, et les simulations à hautes températures montrent des résultats de processus d'échange multiple, mais qui n'ont pas pu être vérifiés à ce jour.

Les mécanismes et les coefficients de diffusion superficielle sont affectés par plusieurs facteurs, comme la force de la liaison chimique surface-adparticule, l'orientation du cristal sur le réseau de surface, les forces attractives et répulsives existantes, et les gradients de potentiel chimique. Les transitions de phases, la croissance par épitaxie, la catalyse hétérogène sont des notions importantes de la science des surfaces. Les phénomènes de diffusion des surfaces sont primordiaux pour l'industrie chimique et des semi-conducteurs. De nombreuses applications sont fondées sur la compréhension de ces phénomènes, on peut notamment citer les pots catalytiques, les circuits intégrés, ou encore l'halogénure d'argent dans les pellicules photographiques.

Aspects cinétiques

Figure 2. Diagramme d'énergie de diffusion en une dimension. x est le déplacement ; E(x) est l'énergie ; Q est la chaleur d'adsorption ; a est l'espace entre deux sites d'adsorption adjacent ; E_diff est la barrière de diffusion.

Les aspects cinétiques de la diffusion superficielle peuvent être considérés par des adatomes résidant dans les sites d'adsorption, sur un réseau à deux dimensions, et se déplaçant vers les sites adjacents (les plus proches voisins) par des processus de saut. La fréquence de saut est caractérisée par une fréquence d'essai et un facteur thermodynamique, lequel détermine la probabilité qu'un essai se concrétise en processus de saut. La fréquence d'essai ν est prise égale à la celle de vibration moléculaire de l'adatome, tandis que le facteur thermodynamique est le facteur de Boltzmann dépendant de la température et de l'énergie potentielle de la barrière de diffusion E_diff.

Le fréquence de saut est alors donnée par :

où

• ν est la fréquence d'essai ;
• E_diff l'énergie potentielle de la barrière ;
• Γ la fréquence de saut ;
• T la température ;
• et k_B la constante de Boltzmann.

E_diff doit être plus petit que l'énergie de désorption afin que la diffusion se produise au lieu du processus de désorption. L'équation 1 montre clairement l'influence de la température sur la fréquence de saut. La manière selon laquelle la diffusion a lieu dépend de la relation entre E_diff et k_BT. Lorsque E_diff est plus petit que k_BT, le facteur thermodynamique est proche de l'unité, et E_diff n'est alors plus une barrière significative à franchir. Ce case est nommé diffusion mobile, est peu commun et a été observé dans seulement quelques systèmes.

Dans la suite de l'article, on considère E_diff ≫ k_BT, et donc . Dans le cas d'une diffusion de Fick, il est possible d'extraire à la fois ν et E_diff d'un diagramme de Arrhenius, c'est-à-dire un diagramme représentant le logarithme du coefficient de diffusion D en fonction de 1/T.

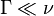
Pour les cas, où il y a plus d'un mécanisme de diffusion qui intervient, il peut y avoir plusieurs E_diff et la distribution entre les différents processus peut changer avec la température.

Les statistiques de marche au hasard décrivent le déplacement quadratique moyen lors de la diffusion en termes de nombre de saut N et de distance a. Le nombre de sauts réussis est simplement Γ multiplié par le temps autorisé par diffusion, t. Dans la plupart des modèles de base, seulement les sauts adjacents sont considérés et a correspond à la distance entre deux sites d'adsorption. Le déplacement quadratique moyen est défini par :

Le coefficient de diffusion est donné par :

où z = 2 pour une diffusion à une dimension, comme par exemple pour une diffusion in-channel ; z = 4 pour un réseau carré ; z = 4 pour un réseau hexagonal.