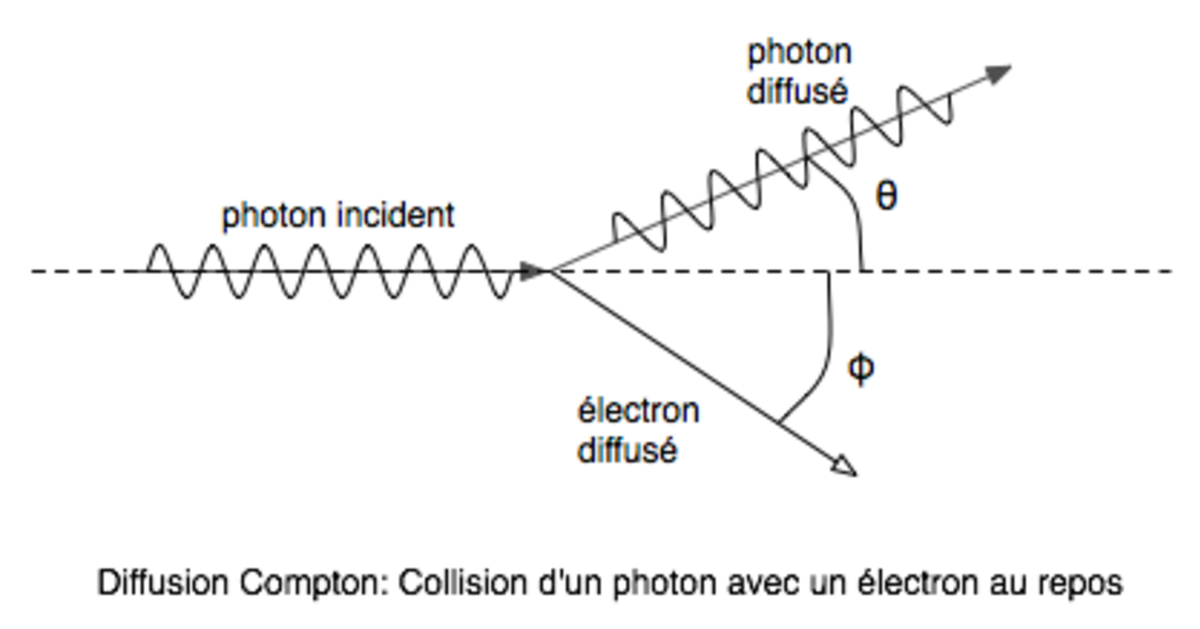
Diffusion élastique de rayonnement - Définition
La liste des auteurs de cet article est disponible ici.
Facteur de forme
Très souvent l'information clé à laquelle l'expérimentateur souhaite accéder, concerne la structure ou la conformation des objets constituant l'échantillon étudié. Cette information est contenue dans le facteur de forme.
Objets à symétrie sphérique
La fonction φ1, qui décrit la façon dont la matière est répartie dans l'objet, n'est fonction que de la distance r au centre de masse. Par ailleurs, à chaque vecteur
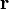
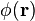
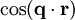
![\begin{array}{rcl} TF(\phi_1(\mathbf{r})) & = & \displaystyle{\int_V d\mathbf{r}\phi_1(\mathbf{r})e^{i\mathbf{q}\cdot\mathbf{r}} = \int_Vd\mathbf{r}\phi_1(\mathbf{r})\cos(\mathbf{q}\cdot\mathbf{r})}\\[2ex] ~ & = & \displaystyle{\int_0^\infty dr 4\pi r^2 \phi_1(r)\int_0^{\pi/2}\cos(qr\cos(\varphi))\sin(\varphi)d\varphi}\\[2ex] ~ & = & \displaystyle{\int_0^\infty dr 4\pi r^2 \phi_1(r)\frac{\sin(qr)}{qr}} \end{array}](https://static.techno-science.net/illustration/Definitions/autres/b/b3c75518c2a00359bc4864f5712e360f_e228462a2315506e3820f2007fa3e991.png)
d'où pour le facteur de forme :
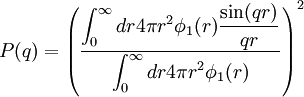
Il faut souligner que qr désigne le produit des normes des vecteur
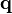
Pour une sphère de rayon R, on obtient :
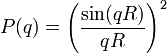
Objets ayant des orientations aléatoires
Dans certains cas, par exemple pour une solution de macromolécules, les objets sont libres de tourner autour de leur centre de masse. Le facteur de forme mesuré est une moyenne sur toutes les orientations possibles d'un objet par rapport au vecteur
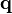
Rayon de giration
Dans le cas où les objets ont en moyenne une symétrie sphérique (cf. les deux cas précédents), le développement limité:
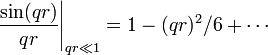
utilisé dans l'expression du facteur de forme donne:
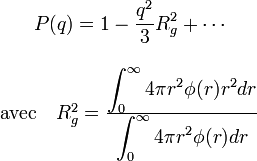
le domaine de vecteur de diffusion pour lequel la condition
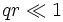
La grandeur Rg a la dimension d'une longueur. C'est la moyenne quadratique des distances au centre de masse de l'objet. C'est le rayon de la sphère ayant le même moment d'inertie que l'objet. Ce rayon "moyen" est appelé rayon de giration de l'objet.
Pour une boule de rayon R et de densité uniforme, on obtient . Pour une sphère, Rg = R.