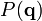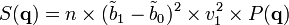Diffusion élastique de rayonnement - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
La diffusion élastique de rayonnement est une technique de mesure physique permettant d'accéder à certaines propriétés structurales de la matière condensée (liquides, solides).
Principes généraux
Diffusion élastique d'une onde plane, longueur de diffusion
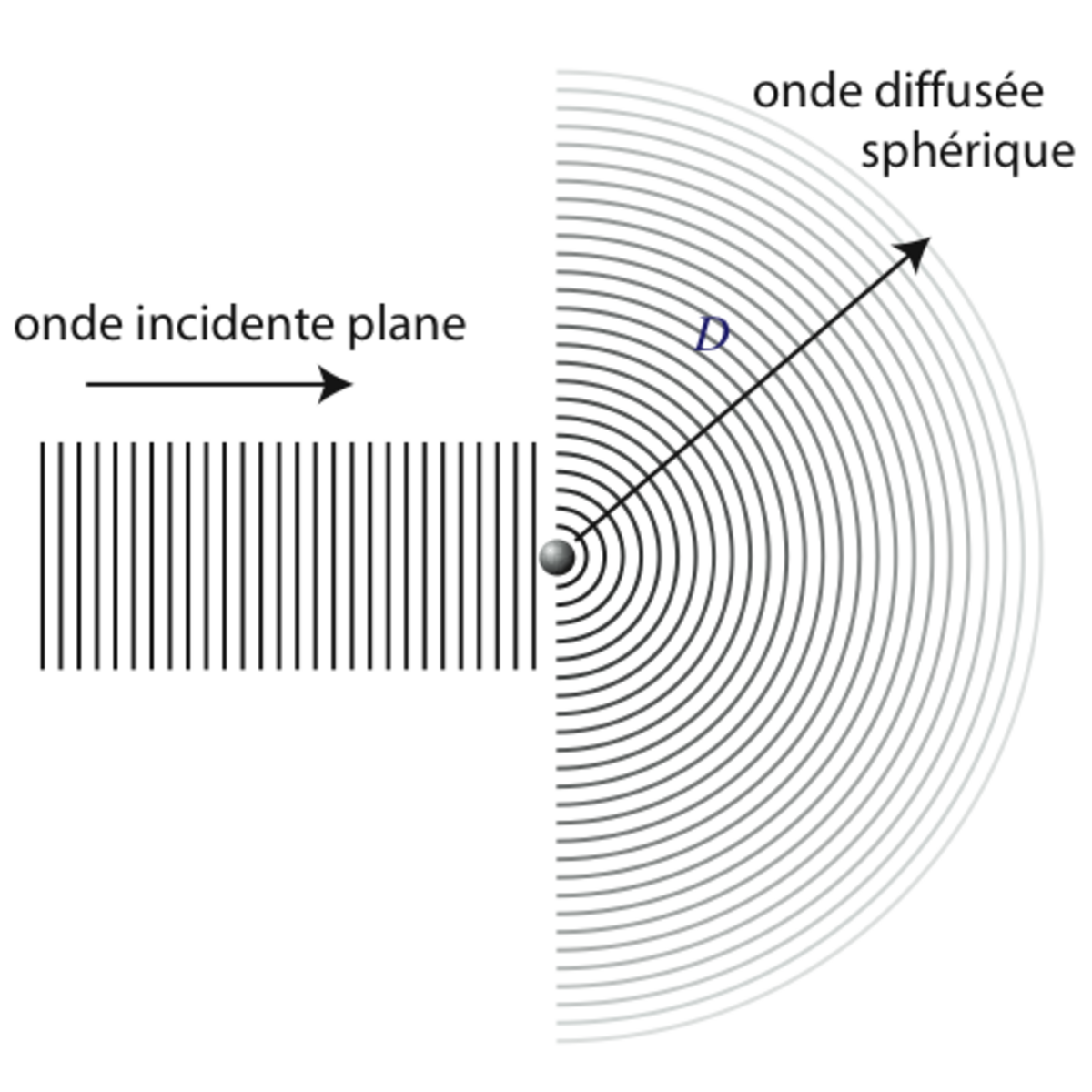
Lors d'une expérience de diffusion de rayonnement, une onde plane incidente ψi de vecteur d'onde ki, (par exemple une faisceau monochromatique de lumière, de rayons X ou de neutrons) éclaire un échantillon. En rencontrant un atome, une partie de cette onde diffuse dans toutes les directions: l'onde diffusée, ψd, est sphérique et son amplitude varie comme l'inverse de la distance D au centre diffuseur. L'amplitude de l'onde diffusée s'écrit donc:
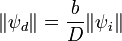
La grandeur b est appelée "longueur de diffusion" et représente la taille de l'atome vue par le rayonnement.
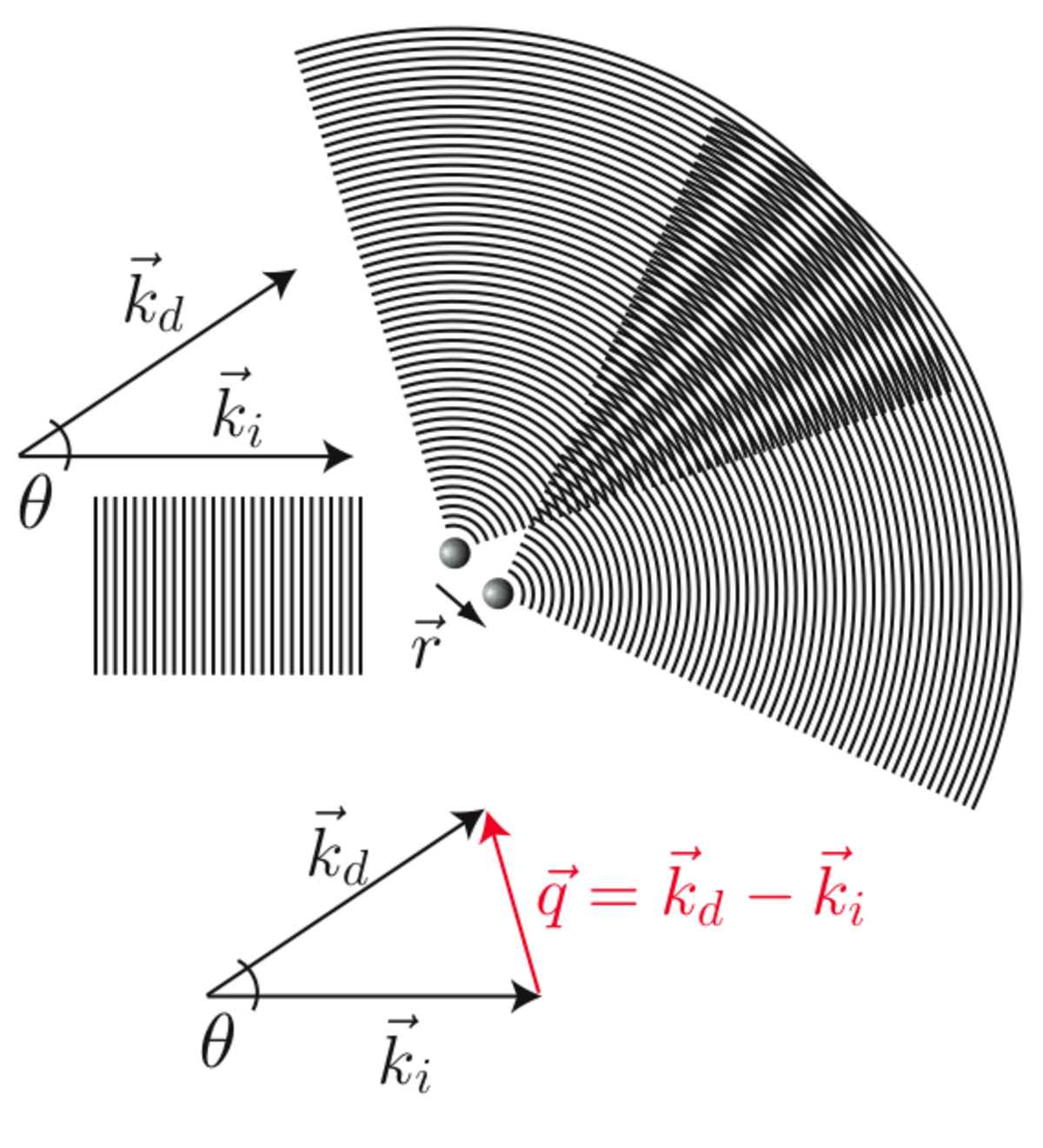
Dans l'hypothèse d'une diffusion élastique, l'onde incidente (de vecteur d'onde ki) et l'onde diffusée (de vecteur d'onde kd) ont la même longueur d'onde λ. Les deux vecteurs d'onde ont la même norme:
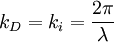
Interférences
Les ondes diffusées par plusieurs atomes interfèrent. L'onde mesurée selon un angle θ, auquel correspond un vecteur d'onde
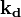
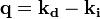
ayant pour norme:
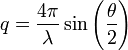
Si ψ(0) est l'onde diffusée par un atome pris pour origine, l'onde diffusée par l'atome situé en un lieu
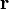
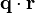
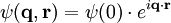
L'onde ψd résultant de la diffusion de tous les atomes a de l'échantillon est la somme des ondes ψa diffusées par chacun:
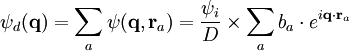
Plutôt que de considérer les atomes, il est possible d'écrire la même expression pour les éléments de volume de l'échantillon de volume total V. La longueur de diffusion,
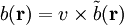
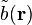
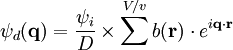
ψd apparaît donc comme la décomposition en série de Fourier de la longueur de diffusion
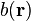
Intensité diffusée
Un détecteur ne mesure pas directement l'onde diffusée mais son intensité qui est son carré:
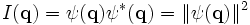
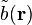
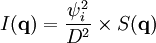
avec
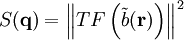
La grandeur
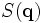
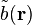

où V est le volume de l'échantillon. Dans cette expression, les crochets représentent la moyenne sur toutes les origines O et sur tous les états microscopiques possibles par lesquels passe l’échantillon.
Le vecteur
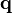
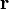
Un milieu homogène ne diffuse pas
Un milieu homogène correspond à
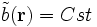
Différence entre diffusion et diffraction
Un milieu homogène est une vue de l'esprit, il existe toujours une échelle spatiale à laquelle des hétérogénéités existent. Par exemple, un cristal parfait observé à l'échelle atomique (grand
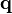
Le terme diffusion concerne des échelles plus grandes comprises entre q = 0 et l'inverse de la distance interatomique (typiquement 1 Å-1). Pour des rayonnements de relativement faible longueur d'onde (rayons X, neutrons), ces échelles d'observation correspondent à des petits angles de diffusion (quelques degrés). D'où le terme de diffusion aux petits angles souvent employé.
Les hétérogénéités responsables de la diffusion
L'intensité diffusée par un échantillon est uniquement due aux variations temporelles ou spatiales de sa densité de longueur de diffusion.
Diffusion et fluctuations: exemple du gaz parfait
On considère un échantillon constitué d'une seule sorte de diffuseur élémentaire (une seule sorte d'atome par exemple). Pour fixer les idées, on peut imaginer un gaz mais l'argumentation reste valable pour un liquide ou un solide.
Pour un gaz, du fait de l'agitation thermique chaque élément de volume est susceptible de contenir un atome à un instant donné puis aucun l'instant d'après. La densité de longueur de diffusion d'un élément de volume donné fluctue autour d'une valeur moyenne notée  . Si les atomes du gaz ont une densité de longueur de diffusion
. Si les atomes du gaz ont une densité de longueur de diffusion
 . La fonction d'autocorrélation de la densité de longueur de diffusion s'écrit:
. La fonction d'autocorrélation de la densité de longueur de diffusion s'écrit:

où
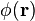
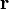
Pour un élément de volume situé en
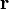
 , est nul en moyenne. Ainsi dans le produit
, est nul en moyenne. Ainsi dans le produit
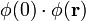
 sont nuls en moyenne. La fonction
sont nuls en moyenne. La fonction  peut donc s'écrire comme la somme de deux termes:
peut donc s'écrire comme la somme de deux termes:

Le premier terme correspond à la diffusion par un milieu homogène de densité de longueur de diffusion  . Sa contribution est nulle. Finalement la mesure n'est sensible qu'aux fluctuations autour de la moyenne:
. Sa contribution est nulle. Finalement la mesure n'est sensible qu'aux fluctuations autour de la moyenne:

Pour un gaz parfait, la fonction d'autocorrélation des fluctuations de densité est nulle sauf pour r = 0. Si les atomes sont très petits par rapport à l'échelle d'observation (
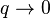
 .
.
où < Δφ2 > est la variance des fluctuations de densité de l'élément de volume v = a3 et a la taille d'un atome ou d'une molécule du gaz. δ est la fonction delta de Dirac. Par transformée de Fourier, on obtient:

La variance < Δφ2 > est directement reliée à la compressibilité isotherme, χT, du gaz:

On obtient le résultat général:

où kT est l'énergie thermique. Pour un gaz parfait, kTχT = kT / P = V / n. Par ailleurs et par définition φ = nv / V, d'où:
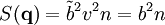
La section efficace différentielle de diffusion est indépendante du vecteur de diffusion (les fluctuations de la densité φ sont l'équivalent d'un bruit blanc) et correspond à la somme des sections efficaces des n atomes du volume de l'échantillon.
Diffusion incohérente et cohérente
Dans le cas d'un gaz parfait, il n'existe aucune corrélation entre les fluctuations de la densité du gaz en un lieu
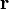
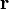
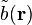
 sont indépendantes et n'ont aucune cohérence de phase. Leurs intensités s'ajoutent. On parle de diffusion incohérente.
sont indépendantes et n'ont aucune cohérence de phase. Leurs intensités s'ajoutent. On parle de diffusion incohérente.
Inversement, lorsque les fluctuations sont corrélées (
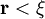
Mélange solvant-soluté
On considère une solution constituée d'un soluté de densité de longueur de diffusion
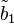
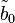
Si le soluté occupe une fraction volumique moyenne φ et le solvant la fraction (1 − φ) complémentaire, alors la densité de longueur de diffusion moyenne est
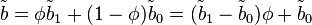
Par contre, en un lieu particulier
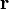
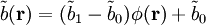
La transformée de Fourier de
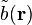
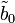
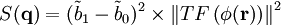
Si la solution est constituée de petites molécules par rapport à l'échelle d'observation, le calcul du paragraphe précédent pourra être repris pour obtenir la fonction de d'autocorrélation de φ(r). Elle fera intervenir la compressibilité osmotique de la solution. Seul change le facteur
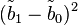
Objets, facteur de forme
Du point de vue de la diffusion de rayonnement, un objet peut être défini comme un volume connexe d'une densité de longueur de diffusion
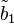
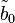
Lorsque la concentration des objets est assez faible pour que leur interdistance moyenne soit supérieure à l'échelle d'observation (1 / q), les interférences dues aux ondes diffusées par des objets différents deviennent négligeables: à la limite, on peut concevoir de n'avoir qu'un seul objet. Pour une population ainsi diluée de n objets, chacun contribue de façon propre à l'intensité diffusée qui est la somme de n termes identiques:
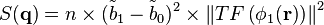
où φ1 désigne la fraction volumique d'un objet.
A q = 0,
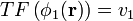
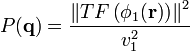
telle que P(0) = 1.