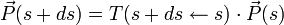Dynamique des faisceaux de particules chargées - Définition

Introduction

La dynamique des faisceaux de particules chargées est une discipline de la physique qui traite du transport et de l'optimisation des caractéristiques des faisceaux dans les accélérateurs de particules.

Le transport d'une particule chargée est décrit dans les champs électromagnétiques produits par l'accélérateur. On peut en déduire les propriétés propres à l'accélérateur (en relation avec un type de particule) qui vont permettre de définir :

• une particule de référence subissant le transport idéal dans l'accélérateur et dont la trajectoire devra être contrainte par les besoins des utilisateurs,
• un formalisme de transport (parfois linéaire) autour de cette particule de référence pour les particules non idéales qui devront demeurer dans une acceptance définie par de nombreux critères (dispersion en taille et divergence, courant perdu admissible). Cette acceptance permet de déterminer les meilleurs conditions d'injection et de transport du faisceau dans l'accélérateur.

Le faisceau de particules est caractérisé par des grandeurs statistiques (par exemple : dimension quadratique moyenne) dont on peut décrire analytiquement l'évolution au cours de l'accélération dans des conditions simplifiées de transport. Une simplification pertinente des paramètres permet une description rapide et très utile du comportement du faisceau pour la définition et le réglage des principaux éléments de l'accélérateur tels que les aimants ou les cavités accélératrices.

Fréquemment, le transport du faisceau à travers l'accélérateur est réalisé à l'aide de logiciels dédiés appelés codes de transport. On peut transporter alors, soit des propriétés statistiques du faisceau, soit un échantillonnage de macro-particules représentant le faisceau, soit la fonction de distribution du faisceau. Ces codes permettent d'accéder au calcul des interactions des particules avec leurs congénères (charge d'espace), le gaz résiduel (diffusion coulombienne, neutralisation, recombinaison) ou avec l'accélérateur (champs induits dans la structure). Ils permettent aussi de vérifier l'influence des imperfections de l'accélérateur sur les propriétés du faisceau.

Transport d'une particule

Représentation d'une particule - Espaces des phases

La dynamique des particules peut être décrite soit dans un référentiel galiléen (Bonne approximation du référentiel du laboratoire), soit dans un référentiel mobile lié à l'accélérateur.

Représentation classique dans un référentiel galiléen

Une particule de masse m et de charge q est décrite, à un instant t, par un point dans un espace des phases à 6 dimensions représentant :

• sa position :

.

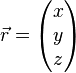
• son déplacement (par exemple, sa quantité de mouvement) :

.

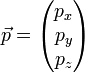
Plus généralement, 6 coordonnées (3 de position, 3 de déplacement) suffisent à décrire la dynamique de la particule en fonction d'une variable indépendante donnée (ici le temps).

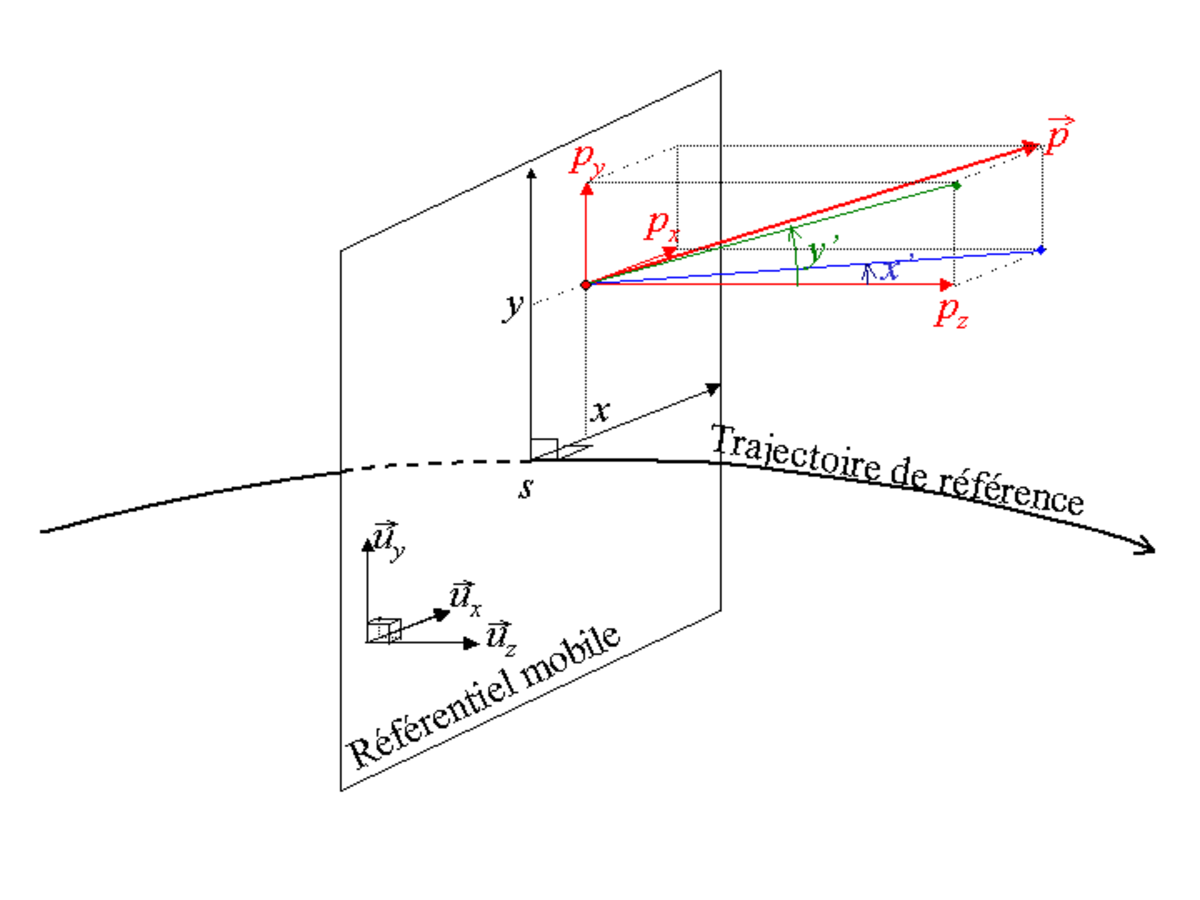
Représentation dans un référentiel mobile

Un accélérateur de particule est conçu de manière à accélérer une particule de référence (dite particule synchrone) qui se propage sur une trajectoire de référence avec une chronométrie bien précise. Cette trajectoire de référence peut être linéaire (linac), circulaire (synchrotron) ou spirale (cyclotron).

• Il est alors très courant de choisir comme variable indépendante, non pas le temps, mais une abscisse s le long de la trajectoire de référence. L'abscisse associée à une particule correspond au point d'intercection entre la trajectoire de référence et le plan normal à cette trajectoire qui contient la particule.

.

• En ce qui concerne sa position, la particule peut être repérée par ses 2 coordonnées (x,y) dans un référentiel mobile contenu le plan transverse à la trajectoire de référence. Généralement x repère la position dans le plan horizontal (plan de déviation du faisceau dans un accélérateur circulaire), y dans le plan vertical. L'autre coordonnée d'espace étant fixée par s, les particules sont finalement différenciées par leur instant de passage à l'abscisse s (comme une photo finish sur la ligne d'arrivée d'une course). Dans la plupart des accélérateurs utilisant des cavités radio-fréquences de fréquence f, cet instant d'arrivée est normalisée par la multiplication par 2π·f. On obtient alors une phase φ qui exprime l'évolution du champ dans les cavités. Il peut alors être pertinent utiliser la différence de phase Φ entre la particule et la particule synchrone.

.

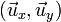
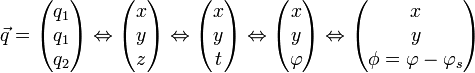
• En ce qui concerne son déplacement, il est usuel de choisir, pour le plan transverse, les 2 pentes x' et y' de la particule par rapport à la trajectoire de référence. L'intérêt porte sur leur mesure et interprétation faciles. Pour la troisième composante du déplacement, on peut trouver, pêle-mêle, la quantité de mouvement p de la particule, la différence relative de la quantité de mouvement de la particule par rapport à celle de la particule synchrone δ, l'énergie cinétique de la particule E ou la différence d'énergie avec la particule synchrone ΔE.

.

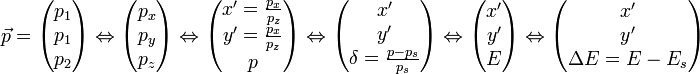
La particule pourra finalement être réprésentée par un vecteur à 6 composantes dont on exprimera l'évolution en fonction de la variable indépendante τ :

.

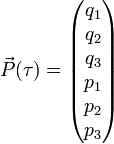
Equations du mouvement

Référentiel du laboratoire (galiléen)

Les équations du transport de la particule dans un champ électromagnétique sont données par la relation fondamentale de la dynamique relativiste :

.

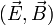
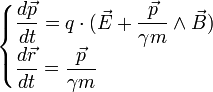
où :

γ est l'énergie réduite de la particule (ou facteur de Lorentz (appellation impropre dans ce cas présent)) reliée à la quantité de mouvement par la relation :

.

c est la constante de la physique correspondant à la vitesse de la lumière dans le vide.

Dans le référentiel galiléen, en utilisant le temps t pour variable indépendante, ces équations s'appliquent directement.

Référentiel mobile

Dans le référentiel mobile, en utilisant l'abscisse s pour variable indépendante, quelques transformations doivent être apportées. Elles sont dues au fait que les vecteurs de la base mobile ne sont pas obligatoirement invariants lors du transport.

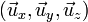
Soit ρ(s), le rayon de courbure de la trajectoire de référence au point s dans le plan (par définition de ). En considérant que ρ>0 si le vecteur pointe vers l'extérieur du virage , nous avons :

.

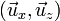
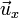
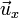
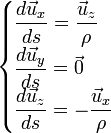
De plus, s étant la projection de la particule sur la trajectoire de référence, nous avons :

.

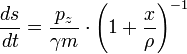
A partir de ces dernières équations et des équations du transport dans le référentiel galiléen, il est possible de déterminer les équations qui donnent les dérivées par rapport à s de chacune des coordonnées des particules dans l'espace des phases choisi.

Quel que soit le référentiel

Finalement, quel que soit le référentiel, si τ est la variable indépendante (t ou s), l'équation vectorielle du transport peut s'écrire :

.

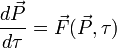
Linéarisation - transport matriciel

Dans ce paragraphe, nous introduisons un formalisme propre aux accélérateurs, et nous choisissons délibérément l'abscisse s pour variable indépendante. La justification est donnée par la suite.

Le traitement le plus simple du transport d'une particule consiste à :

• Utiliser ses coordonnées relatives à la particule synchrone,

.

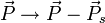
• Linéariser la variation de la force de rappel vers la particules synchrone.

.

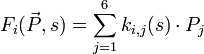
On obtient alors les équations d'évolution des composantes :

.

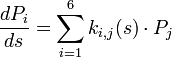
On peut alors utiliser le formalisme matriciel pour transporter la particule d'un point s à un point s+ds :

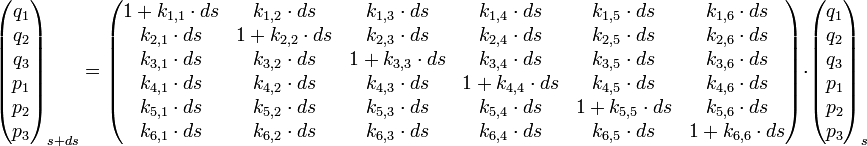
Soit :

Ce formalisme matriciel peut être utilisé pour aller d'un point s₀ à un point s₁:

.

est la matrice de transfert entre le point s₀ et le point s₁.

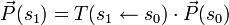
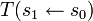
Formellement, elle peut s'obtenir à partir de la multiplication des matrices sur des petits pas ds de s₀ à s₁ (ce qui revient à intégrer pas à pas les équations du transport) :

.

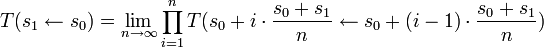
Concrètement, l'accélérateur est découpé en une succession d'éléments E_i dont on connaît les matrices de transfert T_i.

Le transport de l'entrée de l'élément i à la sortie de l'élément j (ou à l'entrée de l'élément j+1, avec j>i) est alors donné par la matrice de transfert :

.

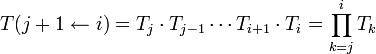
On peut, par cette méthode, transporter les particules élément après élément tout le long de l'accélérateur.

C'est justement parce que les éléments sont positionnés tout le long de l'accélérateur que nous avons choisi l'abscisse s comme variable indépendante. L'utilisation du temps comme variable indépendante pose des difficultés car, à un instant t donné, toutes les particules ne sont pas forcément dans le même élément de l'accélérateur. Il faudrait une matrice par particule !!