Dynamique des faisceaux de particules chargées - Définition

Description statistique d'un faisceau

Distribution des particules d'un faisceau dans deux sous-espaces des phases 2D

Un faisceau est constitué d'un grand nombre de particules. Ce nombre étant souvent très grand, il est généralement impossible de suivre (calculer, mais aussi mesurer) les caractéristiques individuelles de chacune des particules. On réduit alors la description du faisceau à quelques propriétés statistiques qu'il est possible de transporter dans l'accélérateur. Cette représentation statistique du faisceau peut se faire de 3 manières différentes :

• Par une fonction de distribution continue dont on transporte numériquement une discrétisation le long de l'accélérateur. Cette représentation permet aussi, dans certaines conditions, d'obtenir des distributions d'équilibre analytiques pour le faisceau.
• Par des macro-particules, moins nombreuses que le nombre réel de particules, que l'on transporte en résolvant les équations du mouvement des particules (sorte de sondage). Cette technique est essentiellement numérique.
• Par des moments d'ordres plus ou moins élevés de la distribution. Ils pourront être transportés en utilisant des formalismes simples, tels que le formalisme matriciel.

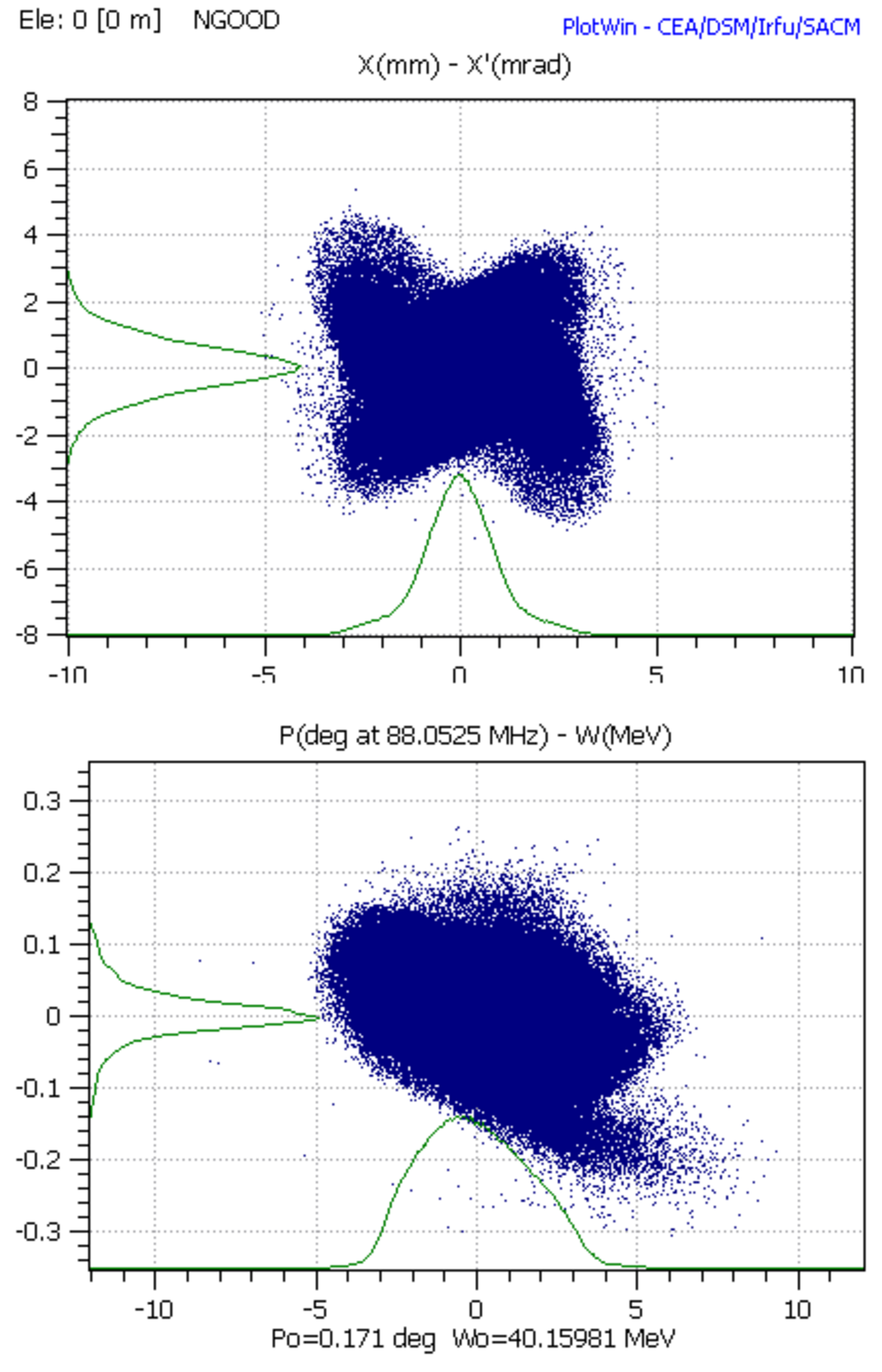
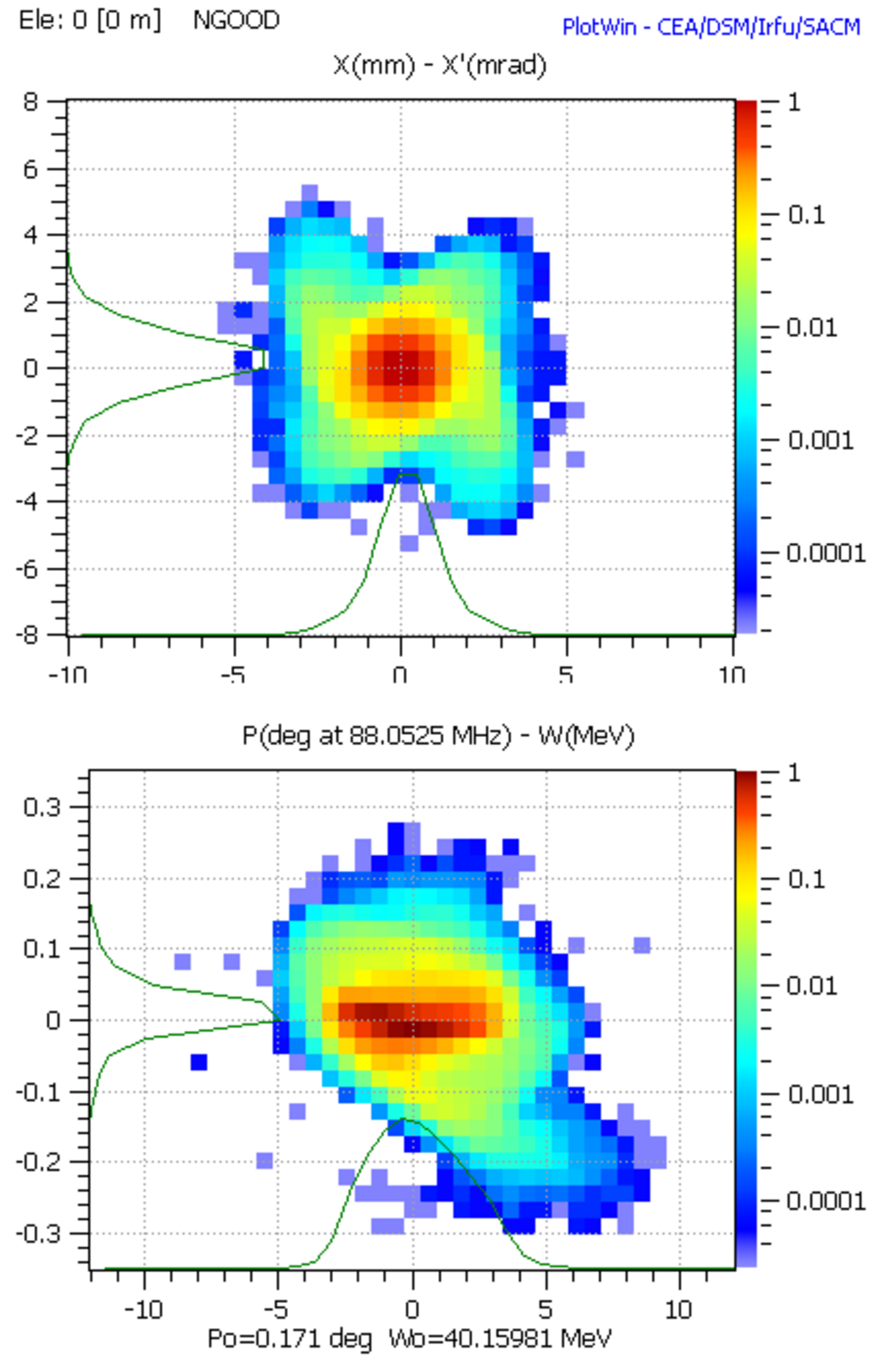
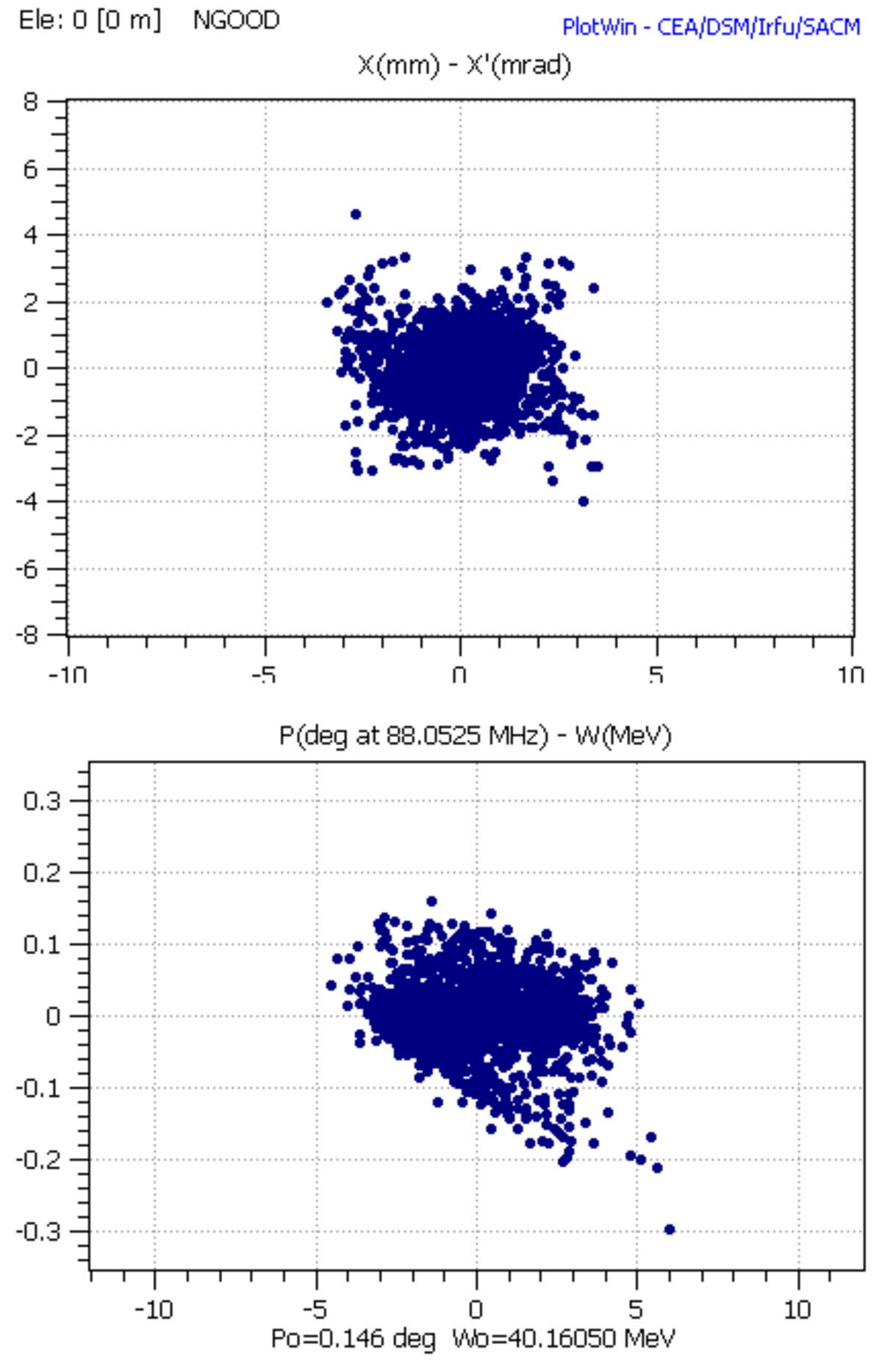
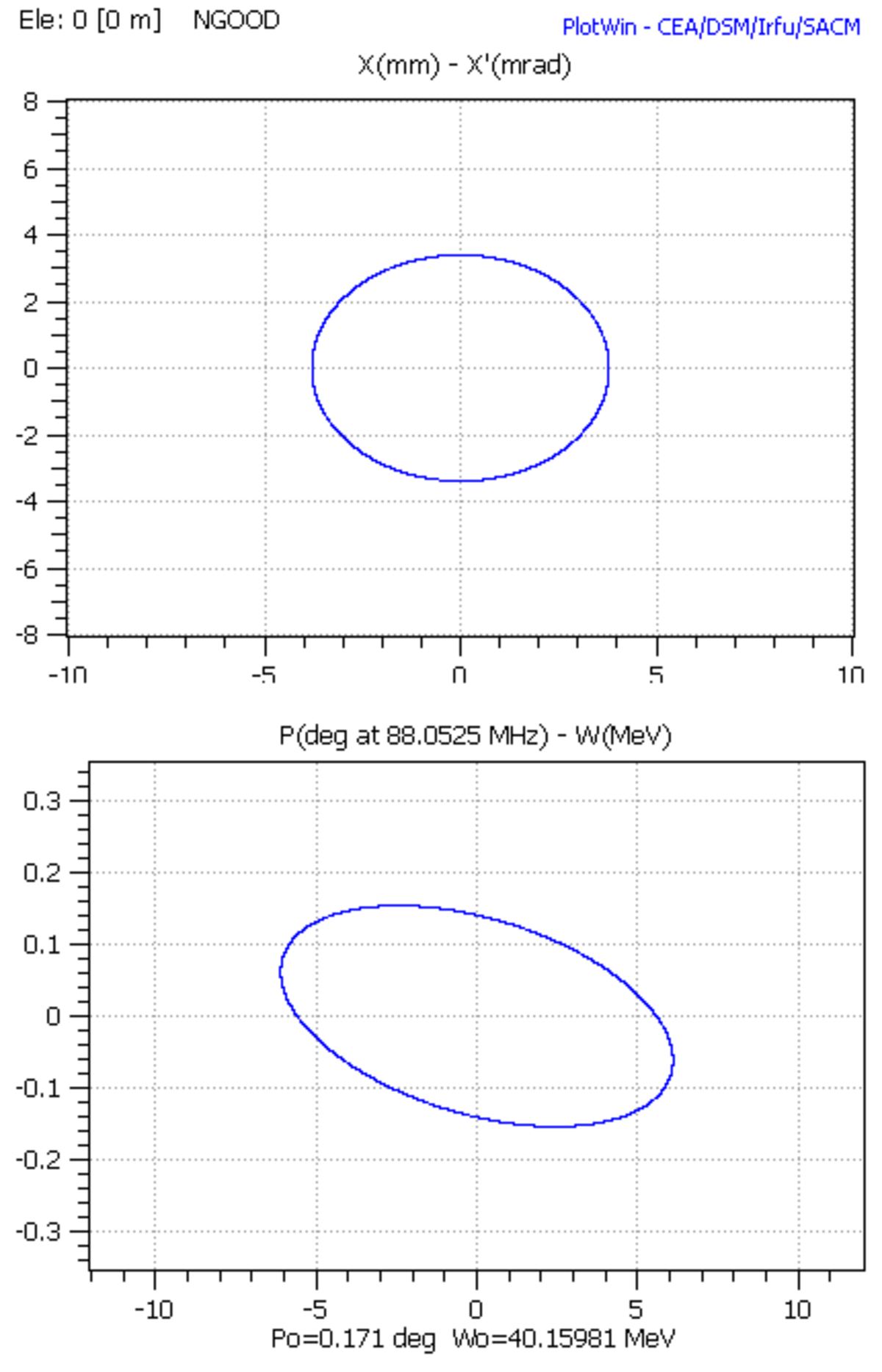
Des illustrations de modélisation issues du code de transport de faisceau TraceWIN sont données à droite.

Elles correspondent à la projection dans 2 sous-espaces des phases (transverse: (x,x') et longitudinal: (phase, Energie)) d'un même faisceau, à une abscisse s donné, pour différents types de modélisation.

Fonction de distribution d'un faisceau dans deux sous-espaces des phases 2D - Echelle logarithmique

Fonction de distribution

Pour une valeur donnée de la variable indépendante τ, un faisceau de particules est défini par la fonction de distribution à 1 corps des particules qui le constituent. Chaque particule pouvant être représentée par 6 coordonnées (3 de position, 3 de déplacement modélisé par le vecteur ), cette fonction de distribution dépend donc de 6 + 1 (variable indépendante) variables. Elle représente la densité de particules dans l'espace des phases 6D (position-déplacement) pour une valeur donnée de τ :

donne le nombre de particules dans le petit hyper-volume de l'espace des phases situé entre et à τ.

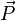
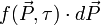
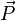
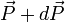
L'évolution de cette fonction de distribution à travers les champs électromagnétiques de l'accélérateur est solution :

• soit de l'équation de Vlasov, si 2 particules "proches" dans l'espace subissent une variation lisse et continue de la force,
• soit l'équation de Fokker-Planck, si les particules "proches" dans l'espace peuvent subir des forces qui diffèrent fortement (collision). Dans ce cas, les termes de Fokker-Planck modélisent ces interactions par une diffusion continue de la fonction de distribution. Cette diffusion correspond à l'effet de nombreuses petites collisions. Cela peut être le cas, par exemple, des collisions coulombiennes particule-particule, des collisions avec le gaz résiduel, ou de l'émission de rayonnement synchrotron.
• soit l'équation de Boltzmann, si la simple modélisation par une diffusion continue ne suffit pas (par exemple, les collisions aux grands angles).

Le choix de l'équation dépendra de la densité, de l'environement ou/et de la durée de vie du faisceau, mais aussi du pas de discrétisation de la fonction de distribution (espace, déplacement et temps ce qui permet de définir la notion de "proche") lors d'une résolution numérique.

Faisceau représenté par des macro-particules dans deux sous-espaces des phases 2D

Macro-particules

Le faisceau, constitué de N particules, est sous-échantillonné par un ensemble de n macro-particules (n<N) qui portent une macro-charge plus forte d'un facteur N/n (pour le calcul des champs induits) mais qui subissent la même dynamique que les particules du faisceau (voir ci-avant).

Le transport de ces macro-particules est simulé à l'aide de logiciels. Les propriétés du faisceau et les champs électromagnétiques induits peuvent être calculés à partir de cet échantillon de macro-particules.

NB : Même si on pouvait simuler N particules, cela resterait un modèle statistique car les conditions initiales réelles de chaque particule ne peuvent jamais être mesurées et sont, de toute manière, non reproductibles.

Moments de la distribution

A partir de la distribution des particules, il est possible de calculer, pour τ donnée, la valeur moyenne d'une fonction A des coordonnées de l'espace des phases :

.

Faisceau représenté par un ellispoïde déduit de ses moments d'ordre 1 et 2 dans deux sous-espaces des phases 2D

Les 6 coordonnées du centre de gravité du faisceau dans l'espace des phases sont données par les moments d'ordre 1 de la distribution :

;

Les dimensions quadratiques moyennes du faisceau dans l'espace des phases sont données par les moments d'ordre 2 centrés de la distribution :

.

Elles correspondent, pour chaque direction de l'espace des phases, à la racine carrée de la moyenne des carrés des distances de toutes les particules au centre de gravité du faisceau. Elles ont la dimension de l'espace des phases. Elles sont d'autant plus grandes que la distribution est étalée dans l'espace des phases. En ce sens, elles donnent une "mesure" de l'étalement de la distribution des particules.

Le faisceau peut être défini par une matrice 6×6, notée σ, donnant l'ensemble des moments d'ordre 2 centrés de la distributions des particules :

.

Cette matrice est symétrique. On retrouve le carré des dimensions quadratiques moyennes sur sa diagonale. D'un point de vue statistique, il s'agit de la matrice de covariance de la distribution du faisceau.