Endomorphisme de Frobenius - Définition
La liste des auteurs de cet article est disponible ici.
Propriétés
Morphisme
- L'endomorphisme de Frobenius est un morphisme d'anneau.
Les propriétés de morphismes multiplicatifs sont évidentes, en effet, comme l'anneau est commutatif:
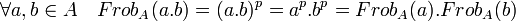
De plus si a est un élément inversible de l'anneau, alors:
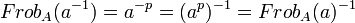
Pour la structure de groupe additif la formule du binôme de Newton montre l'égalité suivante:
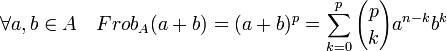
Or l'analyse des diviseurs des coefficient binomiaux montre que tous sont des multiples de p à l'exception du premier et du dernier (cf Diviseurs et coefficients binomiaux). Ce résultat est la conséquence de l'égalité suivante, comme p ne divise pas k il divise le coefficient du binôme d'après le lemme d'Euclide :
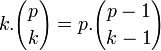
Cette propriété montre que:
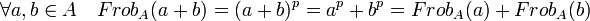
Si p est différent de deux, alors comme il est premier il n'est pas multiple de 2. En conséquence:
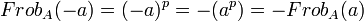
Si p est égal à deux, alors tout élément est égal à son opposé et FrobA(-a) est encore égal à -FrobA(a).
Injectivité et surjectivité
- Si l'anneau A est intègre alors l'endomorphisme de Frobenius est injectif.
Si l'anneau est intègre, alors par définition zéro n'admet pas de diviseur autre que lui-même. En conséquence une puissance d'un élément est nul si et seulement si cet élément est nul.
Dans le cas ou la structure est finie, alors l'injectivité impose la surjectivité car l'ensemble de départ est le même que celui d'arrivée. L'application est alors une permutation. Ce qui démontre la proposition suivante:
- Si l'anneau A est intègre et fini, l'endormorphisme est une bijection. On parle alors d'automorphisme de Frobenius
Point fixe
Le corps premier
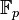
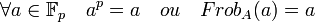
La démonstration est la même que celle du petit théorème de Fermat, le théorème de Lagrange indique que tout sous-groupe d'un groupe fini divise le cardinal du groupe. En conséquence le groupe monogène engendré par a, un élément du corps premier, est un groupe d'ordre d un diviseur de p -1 et ad = 1 et donc ap-1 = 1.
- Tout élément du corps premier est invariant par l'endormorphisme de Frobenius.
Dans le cas ou l'anneau est intègre, alors le polynôme Xp - X ne peut posséder plus de racines que son degré. Il possède donc exactement les racines de son corps premier.
- Si l'anneau est intègre les seuls points fixes de l'endormorphisme de Frobenius sont les éléments du corps premier.
Une conséquence directe est le fait suivant:
- L'endormorphisme de Frobenius est un endomorphisme d'espace vectoriel sur A ou A est considéré comme un
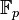
La dernière proposition se traduit de la manière suivante:
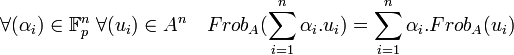
Cette dernière égalité donne l'identité remarquable sur les polynômes à coefficients dans
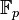
![\forall P[X] \in \mathbb F_p[X] \quad P[X^p]=(P[X])^p](https://static.techno-science.net/illustration/Definitions/autres/0/0b9e6f1be310f123987a783627e3a8aa_92da78b5ac63f996fcbb87c09f59bcdd.png)
Théorie de Galois
Dans le cas des corps commutatifs de caractéristique p ou p est premier, l'endomorphisme de Frobenius apparaît comme un élément du groupe de Galois. Comme ce groupe est essentiel à la compréhension de la structure du corps. Il représente un outil largement utilisé.
Dans le cas des corps finis, toutes les extensions sont séparables d'après le paragraphe précédent, elles sont aussi normales et donc en conséquence galoisiennes. L'automorphisme de Frobenius apparaît alors comme le générateur du groupe de Galois. Cette raison amène la définition suivante:
- Un élément de Frobenius est un élément du groupe engendré par l'endomorphisme de Frobenius.
Tout élément du groupe de Galois est donc un élément de Frobenius dans le cas des corps finis. Si le corps est fini, alors il est une extension finie de
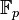
Le sous-corps des éléments invariants par un élément de Frobenius d'ordre l est le sous-corps
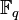
Dans le cas des extensions infinies, les éléments de Frobenius jouent aussi un rôle majeur. Ils sont particulièrement utilisés pour comprendre comment les idéaux premiers se décomposent dans les extensions abéliennes.