Extension quadratique - Définition

Définition

• Soit K un corps, L une extension de corps de K. L'extension L est dite quadratique si et seulement si la dimension de L comme espace vectoriel sur K est 2. Si α est un élément de L qui n'est pas élément de K, alors l'extension est souvent notée K(α).

• Un élément d'une extension L sur K est dit quadratique s'il est inclus dans une extension quadratique de K.

Remarque: K(α) désigne le plus petit corps contenant α, il est donc engendré par les puissances de α. Dans le cas d'une extension quadratique, tout élément de L est combinaison linéaire de 1 et α, car l'espace est de dimension 2 et que 1 et α forment une famille libre car α n'est pas élément de K.

Remarque: Toute extension de corps est un espace vectoriel sur son corps de base. Cette propriété n'est pas spécifique aux extensions quadratiques.'

Propriétés galoisiennes

Dans ce paragraphe L désigne une extension quadratique du corps K de caractéristique différente de 2.

Séparation

• L'extension L est séparable.

Si dans un corps, on additionne plusieurs fois de suite l'unité, il est possible de trouver zéro. C'est par exemple toujours le cas si le corps est de cardinal fini. Dans le cas où les sommes successives de l'unité ne sont jamais nulles alors on parle de caractéristique nulle. C'est par exemple le cas pour les corps des nombres rationnels, réels ou complexes.

Dire que l'extension L est séparable, c'est dire que les polynômes minimaux n'ont jamais de racines multiples. Cette propriété est importante pour la théorie de Galois. Elle apparaît dans la suite de l'analyse des propriétés des extensions quadratiques. Soit l un élément de L et P[X] son polynôme minimal à coefficient dans K. On suppose que l n'est pas élément de K car sinon son polynôme est de degré 1 est il n'existe évidemment pas de racine multiple. Alors P[X] est de degré deux. Sa dérivée est de degré un à coefficient dans K car P[X] est à coefficients dans K. Comme l n'est pas élément de K, l ne peut être racine de la dérivée. Or une racine est multiple si et seulement si elle est aussi racine du polynôme dérivée.

Ce raisonnement ne s'applique pas en caractéristique deux. considérons en effet un polynôme de la forme X² - c, ou c est un élément de K, sa dérivé est toujours nulle donc toute racine carrée possède un polynôme minimal non séparable.

Groupe de Galois

Le groupe de Galois est le groupe des automorphismes de corps de L laissant K invariant. Si l'extension est séparable, elle est dite de Galois si et seulement si elle est aussi extension normale, c'est-à-dire si tout morphisme de corps de L dans une clôture algébrique a pour image L. Une clôture algébrique est une extension de K tel que tout polynôme à coefficients dans la clôture admet au moins une racine. Par exemple, le corps des complexes est une clôture algébrique des nombres réels. On démontre d'ailleurs que c'est la seule (cf la preuve par la théorie de Galois du théorème de d'Alembert-Gauss). Une propriété démontrée dans l'article détaillé montre qu'une extension séparable L est galoisienne si et seulement si le groupe de Galois contient autant d'élément que la dimension de L sur K.

• Il existe exactement deux automorphismes de corps de l'extension quadratique L, laissant K invariant.

En effet, soit d un élément de K tel que L est égal à K[√d] et σ un automorphisme de L différent de l'identité et laissant invariant K. Pour tout élément de K L'application σ est aussi un automorphisme de K espace vectoriel. Par définition σ laisse K stable donc l'image de d est égal à d. On en déduit que σ (√d²) égal à σ (√d)² est égal à d et donc σ (√d) est égal à + ou - √d.

La famille (1, √d) est une base du K espace vectoriel L, l'image de 1 par σ est égal à 1 car K est stable par σ et 1 est élément de K. Le fait que σ est différent de l'identité montre que σ (√d) est égal à -√d. On en déduit que σ est défini par :

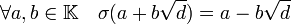
• L'automorphisme σ, laissant invariant K et tel que l'image de √d est égal à -√d est appelée application conjugué de L sur K.

On vérifie que l'application définie par l'égalité précédente est bien un automorphisme de corps.

• L'extension L sur K est normale, galoisienne et abélienne.

En effet, le groupe de Galois de l'extension L sur K contient deux éléments, l'identité et σ . Une proposition démontrée dans l'article détaillée montre que toute extension séparable dont le groupe de Galois contient autant d'éléments que la dimension de L sur K est normale et galoisienne. Le groupe de Galois contient deux éléments, il est donc abélien et l'extension L est abélienne.