Extension quadratique - Définition

Entier quadratique

Un des intérêts des extensions quadratiques est la résolution d'équations diophantiennes. Celles du grand théorème de Fermat, de Pell-Fermat ou des deux carrés en sont des exemples. Une partie uniquement de l'extension est considérée, celles des entiers algébriques. Soit d est un entier sans facteur carré, un élément u de Q(√d) est dit entier si et seulement s'il existe un polynôme unitaire et à coefficients entiers admettant u pour racine.

Corps quadratique et corps cyclotomique

Il existe un unique corps quadratique inclus dans le corps cyclotomique engendré par une racine primitive p-ième de l'unité, avec p, un nombre premier impair : en effet, le corps cyclotomique est une extension cyclique du corps des rationnels, de degré pair p-1, et la théorie de Galois assure l'existence et l'unicité souhaitées. Le discriminant du corps quadratique est p pour et - p pour  : en effet, les seules places ramifiées dans le corps cyclotomique sont la place p et la place à l'infini, ce sont donc les seules susceptibles de se ramifier dans le corps quadratique, et, comme noté ci-dessus, tout nombre premier divisant le discriminant réduit d'un corps quadratique est ramifié dans ce corps.

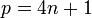
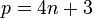
Un corps cyclotomique engendré par une racine n-ème de l'unité, pour n non premier admettent en revanche par la théorie de Galois plusieurs sous-corps quadratiques (non cyclicité du groupe de Galois).