Extension quadratique - Définition

Construction d'une extension quadratique

Cas général

Soit d un élément de K tel qu'il n'existe aucun élément de K dont le carré est égal à d. Le polynôme P(X) égal à X² - d n'admet pas de racine et est donc irréductible dans K. Un raisonnement analogue à celui du troisième exemple montre que le quotient K[X]/P(X) de l'espace des polynômes par l'idéal engendré par P(X) est un corps, noté ici L. Soit Q(X) un polynôme à coefficients dans K, la division euclidienne de Q(X) par P(X) montre qu'il est congru à un polynôme du premier degré. Tout élément de L admet donc comme représentant un polynôme du premier degré. Un exemple de cette nature est donnée dans l'article Indéterminée.

L'application de K dans L qui à k associe sa classe est un plongement de K dans L, c'est-à-dire un morphisme injectif de corps. Il est donc possible d'identifier K avec une partie de L, celle des classes de K. Si la classe du monôme X est noté √d, alors tout élément de L est combinaison linéaire de 1 et de √d, car tout élément de L possède pour représentant un polynôme de degré 1. Pour cette raison, l'extension est souvent noté K(√d). L est un K espace vectoriel engendré par une famille de deux éléments, 1 et √d, cette famille est libre car, par hypothèse √d n'est pas un élément de K. Le corps L est bien une extension quadratique de K.

Réciproquement, soit M une extension quadratique quelconque de K. Soit z un élément de M qui n'est pas élément de K. La famille (1, z) est une base de M, en tant que K espace vectoriel, car elle est libre et de cardinal égal à la dimension de l'espace. L'élément z² est combinaison linéaire de 1 et de z et il existe -b et -c deux élément de K tel que : z² + b.z + c est égal à 0. On en déduit l'égalité :

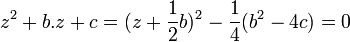
Comme K n'est pas de caractéristique 2, 2 et 4 sont bien des éléments différents de 0 donc inversibles. Notons d la valeur (b² - 4.c)/4. Le fait que b et c soit éléments de K montre que d l'est aussi. Soit δ l'élément de M égal à z + b/2, on remarque que δ n'est pas élément de K car z ne l'est pas et δ² est égal à d. On en déduit que d n'a pas de racine dans K.

Le polynôme P(X) = X² - d est irréductible. Considérons alors L le quotient K[X]/P(X). Pour les mêmes raisons que précédemment, L est un corps, noté K(√d). Un calcul élémentaire montre qu'il existe un automorphisme de corps de M dans L qui à δ associe √d. Ce qui montre la proposition suivante :

• Soit L une extension quadratique de K, il existe un élément d de K qui n'admet pas de racine carrée dans K tel que L est isomorphe à K(√d).

Cas des rationnels

Un cas souvent utilisé en arithmétique est celui où K est égal à Q, l'ensemble des rationnels. La propriété précédente prend une forme un peu plus forte :

• Soit L une extension quadratique de Q, il existe un unique entier d sans facteur carré tel que L est égal à Q(√d).

Un entier est dit sans facteur carré si sa décomposition en facteurs premiers ne comporte que des exposants égaux à un.

Remarque : Le symbole √ porte une double signification. Soit il désigne une fonction des réels positifs vers les réels positifs, soit il désigne la classe de X dans le quotient défini précédemment. La première définition ne peut se généraliser aux nombres négatifs. En effet, √-1 n'a pas de racine dans R, l'ensemble des réels et en possède deux dans celui des complexes. Si l'approche algébrique permet de définir rigoureusement √-1, tel n'est pas le cas de la deuxième. Pour cette raison, si d est strictement positif, √-d est aussi noté i√d, avec i désignant l'unité imaginaire. L'extension est alors identifiée avec un sous-corps des nombres complexes.

• Existence :

Soit deux entiers p et q tel que p/q est égal à d. Il est possible de multiplier d est aussi égal à p.q /q², en conséquence, Q(√d) est égal à Q(√p.q) et toute extension quadratique de Q s'exprime comme une extension d'un radical entier.

L'entier p.q s'exprime comme le produit de deux facteurs, l'un contenant tous les facteurs carrés et l'autre sans facteur carré. Il existe ainsi deux entiers n et m tel que p.q = n².m. On remarque alors que Q(√d) est égal à Q(√n) et l'entier n ne contient aucun facteur carré.

• Unicité :

Soit d₁ et d₂ deux entiers sans facteur carré, tel que les deux extensions soient confondues. Alors :

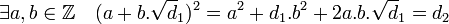
On en déduit que 2.a.b est égal à 0 et a² + d₁.b² = d₂. L'entier b ne peut être nul, d₂ serait alors un carré. En conséquence a est nul et comme d₂ ne contient aucun facteur carré b est égal à 1 donc d₁ est égal à d₂. Ce qui montre l'unicité.