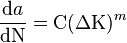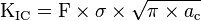Fatigue (matériau) - Définition

Introduction

La fatigue est un processus (succession de mécanismes) qui sous l'action de contraintes ou déformations variables dans le temps modifie les propriétés locales d’un matériau et peut entraîner la formation de fissures et éventuellement la rupture de la structure. La fatigue est notamment caractérisée par une étendue de variation de contrainte bien inférieure à la résistance à la traction du matériau. Les étapes principales de la fatigue sont l’amorçage de fissures (si des défauts ne sont pas déjà présents dans le matériau), la propagation de fissures et la rupture finale. Les paramètres souvent utilisés pour prédire le comportement en fatigue et ainsi le nombre de cycles à rupture d'une structure sont : l'amplitude de cette sollicitation (chargement ou déformation imposée), sa valeur moyenne, le fini de surface et le milieu dans lequel la structure sera utilisée.

Mécanisme

Lorsque l'on exerce une contrainte monotone (voir essai de traction) sur une éprouvette lisse (avec un champ de contrainte quasi uniforme) métallique ductile, celle-ci commence à se déformer de manière irréversible par déformation plastique, à partir d'une valeur de contrainte appelée limite d'élasticité. Bien inférieure à la valeur limite conventionnelle (définie pour une déformation résiduelle de 0.2%), il existe la limite d'endurance. Tout chargement cyclé au-delà de la limite d'endurance endommagera l'éprouvette.

Lorsque l'on analyse une structure dont le champ de contrainte est quelconque, on doit examiner ses différents modes de dégradation.

• la rupture statique ou rupture en 1/4 de cycle.
• la déformation permanente si elle peut obérer le fonctionnement ultérieur.
• la rupture en fatigue oligocyclique, pour des chargements conduisant à la ruine en moins de 50 000 cycles
• la fatigue conventionnelle au-delà de 50 000 cycles.

Ces différents modes de ruine correspondent à des chargements d'amplitudes décroissantes.

L'endommagement en fatigue se produit en priorité dans les zones dont les contraintes alternées sont les plus fortes, c'est-à-dire dans les zones à concentration de contraintes (trous, entailles...).

Si l'on observe la surface rompue au microscope, on a un faciès typique : on voit des stries globalement parallèles, correspondant à la propagation de la fissure à chaque sollicitation, puis une zone d'arrachement, correspondant à la rupture finale.

La durée de vie à l'amorçage de fissure a souvent une durée importante devant celle de propagation. Dans le cas d'une éprouvette lisse, la durée de vie en propagation est faible. En revanche, pour une structure, la partie propagation peut être significative. On distingue donc deux phases :

• la phase d'amorçage durant laquelle le matériau est endommagé de façon non détectable.

La durée de vie est souvent définie à l'amorçage de fissure détectable de la structure, avec un choix approprié des propriétés minimales du matériau.

• la phase de propagation de fissure pendant laquelle des inspections peuvent être effectuées avant rupture.

C'est le domaine de la mécanique de la rupture.

Loi de propagation d'une fissure

Une singularité peut exister dans le matériau, elle peut avoir deux origines :

• un défaut initial de fabrication
• un amorçage d'une fissure détectable dû à la fatigue.

On la caractérise par sa dimension a, et sa forme.

Cette fissure va se propager, donc a va augmenter si le chargement est variable jusqu'à la dimension critique a_c.

La loi de Paris est la loi la plus simple régissant sa propagation. Soient

• N le nombre de cycles ;
• ΔK la variation du facteur d'intensité de contrainte ;
• K, C et m des coefficients dépendant du matériau ;

on a

Sa dimension critique a_c est liée à la caractéristique du matériau K_IC, la ténacité, elle entraîne la rupture fragile de la structure :

où σ est une contrainte effective dans une direction normale à la fissure et F un facteur de forme.