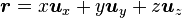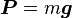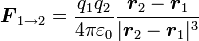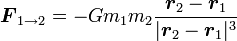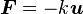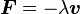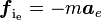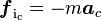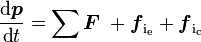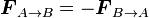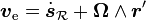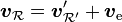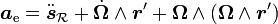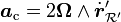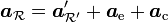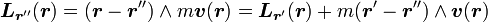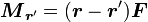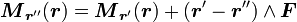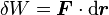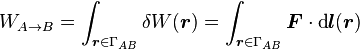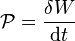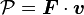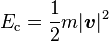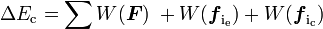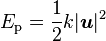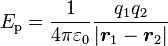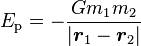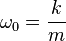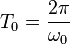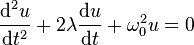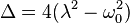Samedi 14 Décembre 2024
Rechercher 🔍

Formulaire de mécanique - Définition

Source: Wikipédia sous licence CC-BY-SA 3.0.
La liste des auteurs de cet article est disponible ici.
- Introduction - Cinématique : le rayon vecteur et ses dérivées successives - Dynamique - Changement de référentiel - Notion de Moment - Aspect énergétique - Oscillateur

Introduction
Optique
Électro- Magnéstatique
Physique quantique
Thermodynamique
Mécanique des fluides
Mécanique
Relativité restreinte
Trou noir
Analyse vectorielle

Cinématique : le rayon vecteur et ses dérivées successives

En coordonnées cartésiennes

\boldsymbol r =x \boldsymbol u_x + y \boldsymbol u_y + z \boldsymbol u_z

La vitesse du point situé en r s'écrit

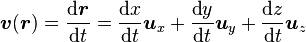
\boldsymbol v (\boldsymbol r) =\frac{ \text{d} \boldsymbol r}{ \text{d} t }=\frac{\text{d} x}{\text{d} t} \boldsymbol u_x + \frac{\text{d} y}{\text{d} t} \boldsymbol u_y + \frac{\text{d} z}{\text{d} t} \boldsymbol u_z ,

et l'accélération

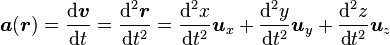
\boldsymbol a(\boldsymbol r)=\frac{\text{d} \boldsymbol v}{\text{d} t}=\frac{\text{d}^2 \boldsymbol r}{\text{d} t^2}=\frac{\text{d}^2 x}{\text{d} t^2} \boldsymbol u_x + \frac{\text{d}^2 y}{\text{d} t^2} \boldsymbol u_y + \frac{\text{d}^2 z}{\text{d} t^2} \boldsymbol u_z .

En coordonnées cylindriques

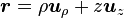
\boldsymbol r=\rho \boldsymbol u_\rho+z \boldsymbol u_z
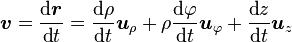
\boldsymbol v=\frac{\text{d} \boldsymbol r}{\text{d} t}= \frac{\text{d} \rho}{\text{d} t} \boldsymbol u_\rho+\rho\frac{\text{d} \varphi}{\text{d} t} \boldsymbol u_\varphi +\frac{\text{d} z}{\text{d}t} \boldsymbol u_z .
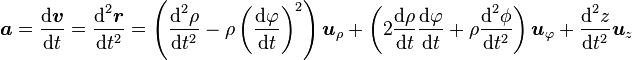
\boldsymbol a =\frac{\text{d} \boldsymbol v}{\text{d} t}=\frac{\text{d}^2 \boldsymbol r}{\text{d}t^2}=\left(\frac{\text{d}^2 \rho}{\text{d} t^2}-\rho\left(\frac{\text{d} \varphi}{\text{d} t}\right)^2\right) \boldsymbol u_\rho+\left(2\frac{\text{d} \rho}{\text{d} t}\frac{\text{d} \varphi}{\text{d} t}+\rho\frac{\text{d}^2 \phi}{\text{d}t^2}\right) \boldsymbol u_\varphi+\frac{\text{d}^2 z}{\text{d}t^2} \boldsymbol u_z .

Ces formules sont basées sur le fait que la dérivée temporelle de deux des vecteurs de base est non nulle :

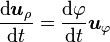
\frac{\text{d} \boldsymbol u_\rho}{\text{d} t}=\frac{\text{d}\varphi}{\text{d}t} \boldsymbol u_\varphi ,
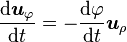
\frac{\text{d} \boldsymbol u_\varphi}{\text{d} t}=-\frac{\text{d}\varphi}{\text{d}t} \boldsymbol u_\rho .

En coordonnées sphériques

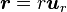
\boldsymbol r=r \boldsymbol u_r ,
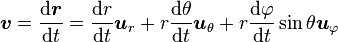
\boldsymbol v =\frac{\text{d} \boldsymbol r}{\text{d} t}=\frac{\text{d}r}{\text{d}t} \boldsymbol u_r+r\frac{\text{d} \theta}{\text{d} t} \boldsymbol u_\theta+r \frac{\text{d}\varphi}{\text{d}t}\sin \theta \boldsymbol u_\varphi ;
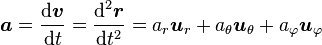
\boldsymbol a =\frac{\text{d} \boldsymbol v }{\text{d} t}=\frac{\text{d}^2 \boldsymbol r}{\text{d}t^2}=a_r \boldsymbol u_r+a_\theta \boldsymbol u_\theta+a_\varphi \boldsymbol u_\varphi ,

avec:

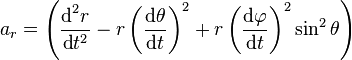
a_r=\left(\frac{\text{d}^2r}{\text{d}t^2}-r\left(\frac{\text{d} \theta}{\text{d} t}\right)^2+r\left(\frac{\text{d}\varphi}{\text{d}t}\right)^2\sin^2\theta\right) ,
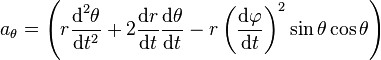
a_\theta=\left( r \frac{\text{d}^2 \theta}{\text{d}t^2} +2\frac{\text{d}r}{\text{d}t} \frac{\text{d} \theta}{\text{d} t}-r\left( \frac{\text{d}\varphi}{\text{d}t} \right)^2\sin \theta \cos \theta\right)
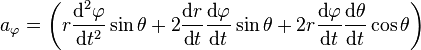
a_\varphi=\left( r \frac{\text{d}^2 \varphi}{\text{d}t^2}\sin \theta +2\frac{\text{d}r}{\text{d}t} \frac{\text{d} \varphi}{\text{d} t}\sin \theta + 2r\frac{\text{d} \varphi}{\text{d} t}\frac{\text{d} \theta}{\text{d} t}\cos \theta\right) .

Dynamique

Quelques forces

  • Poids :
    \boldsymbol P =m \boldsymbol g
  • Interaction électromagnétique :
    \boldsymbol F_{1\rightarrow 2}= \frac{q_1 q_2}{4\pi \varepsilon_0} \frac{\boldsymbol r_2 - \boldsymbol r_1}{|\boldsymbol r_2 - \boldsymbol r_1|^3}
  • Interaction gravitationnelle :
    \boldsymbol F_{1\rightarrow 2}= -G m_1 m_2 \frac{\boldsymbol r_2 - \boldsymbol r_1}{|\boldsymbol r_2 - \boldsymbol r_1|^3}
  • Tension d'un ressort de raideur k et d'allongement u :
    \boldsymbol F = - k \boldsymbol u
  • Frottement fluide :
    \boldsymbol F = -\lambda \boldsymbol v
  • Force d'inertie d'entraînement :
    \boldsymbol f_{\rm i_e}= - m \boldsymbol a_e
  • Force d'inertie de Coriolis:
    \boldsymbol f_{\rm i_c}=-m \boldsymbol a_c

Principe fondamental de la dynamique

  • Vecteur quantité de mouvement :
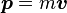
    \boldsymbol p = m \boldsymbol v (en général)
  • Principe fondamental de la dynamique :
    \frac{\text{d} \boldsymbol p}{\text{d}t}= \sum \boldsymbol F \; +\boldsymbol f_{\rm i_e} + \boldsymbol f_{\rm i_c}
  • Principe des actions réciproques : pour deux corps A et B,
    \boldsymbol F_{A \rightarrow B} = - \boldsymbol F_{B \rightarrow A}

Changement de référentiel

Soit un point de rayon vecteur r dans un référentiel \mathcal R . Soit un autre référentiel, \mathcal R ', dont l'origine est située au rayon vecteur s dans \mathcal R . Le rayon vecteur du point, déterminé dans \mathcal R ' est alors

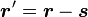
\boldsymbol r' = \boldsymbol r - \boldsymbol s .

Les vitesses du point peuvent être mesurées dans \mathcal R ou dans \mathcal R '. Elles sont notées avec l'indice \mathcal R ou \mathcal R ', de même que les accélérations.

  • Vitesse d'entraînement :
    \boldsymbol v_{\rm e} = \dot \boldsymbol s_{\mathcal R} + \boldsymbol \Omega \wedge \boldsymbol r'
  • Loi de composition des vitesses :
    \boldsymbol v_{\mathcal R} = \boldsymbol v'_{\mathcal R'} + \boldsymbol v_{\rm e}
  • Accélération d'entraînement :
    \boldsymbol a_{\rm e} = \ddot \boldsymbol s_{\mathcal R} + \dot \boldsymbol \Omega \wedge \boldsymbol r' + \boldsymbol \Omega \wedge (\boldsymbol \Omega \wedge \boldsymbol r')
  • Accélération de Coriolis :
    \boldsymbol a_{\rm c} = 2 \boldsymbol \Omega \wedge \dot \boldsymbol r'_{\mathcal R'}
  • Loi de composition des accélérations :
    \boldsymbol a_{\mathcal R} = \boldsymbol a'_{\mathcal R'} + \boldsymbol a_{\rm e} + \boldsymbol a_{\rm c}

Notion de Moment

  • Moment cinétique d'un point r par rapport à un point r' :
  • Par rapport à un autre point r'' :
    \boldsymbol L_{\boldsymbol r''}(\boldsymbol r)= (\boldsymbol r - \boldsymbol r'') \wedge m \boldsymbol v(\boldsymbol r) = \boldsymbol L_{\boldsymbol r'}(\boldsymbol r) + m (\boldsymbol r' - \boldsymbol r'') \wedge \boldsymbol v(\boldsymbol r)
  • Moment d'une force F au point de rayon vecteur r' :
    \boldsymbol M_{\boldsymbol r'} = (\boldsymbol r - \boldsymbol r') \boldsymbol F
  • Par rapport à un autre point r'' :
    \boldsymbol M_{\boldsymbol r''}(\boldsymbol r)= \boldsymbol M_{\boldsymbol r'}(\boldsymbol r) + (\boldsymbol r' - \boldsymbol r'') \wedge \boldsymbol F
  • Théorème du moment cinétique :
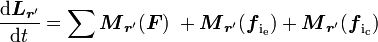
    \frac{\text{d} \boldsymbol L_{\boldsymbol r'}}{\text{d} t}=\sum \boldsymbol M_{\boldsymbol r'} (\boldsymbol F)\;+\boldsymbol M_{\boldsymbol r'}(\boldsymbol f_{\rm i_e})+ \boldsymbol M_{\boldsymbol r'}(\boldsymbol f_{\rm i_c}) .

Aspect énergétique

  • Travail élémentaire d'une force F lors d'un déplacement dr:
    \delta W =\boldsymbol F \cdot\text{d} \boldsymbol r
  • Travail le long d'un chemin ΓAB :
    \displaystyle W_{A \rightarrow B}=\int_{\boldsymbol r \in \Gamma_{AB}} \delta W(\boldsymbol r)=\int_{\boldsymbol r \in \Gamma_{AB}} \boldsymbol F \cdot\text{d} \boldsymbol l(\boldsymbol r)
  • Puissance :
    \mathcal{P}=\displaystyle \frac{\delta W}{\text{d} t}
  • On peut aussi définir la puissance comme étant le produit scalaire de la force appliquée au point M avec la vitesse du point :
    \mathcal{P}= \boldsymbol F \cdot \boldsymbol v
  • Énergie cinétique d'un point matériel :
    E_{\rm c} =\displaystyle \frac{1}{2}m |\boldsymbol v|^2
  • Théorème de l'énergie cinétique :
    \displaystyle \Delta E_{\rm c}=\sum W(\boldsymbol F)\;+W( \boldsymbol f_{\rm i_e})+W(\boldsymbol {f}_{\rm i_c})
  • Énergie mécanique :
    Em = Ec + Ep

Énergie potentielle pour quelques forces conservatives

Chacune de ces énergies est définie à une constante près

  • Pesanteur :
    Ep = mgz
  • Ressort :
    E_{\rm p} = \frac{1}{2}k |\boldsymbol u|^2
  • Force de Coulomb :
    E_{\rm p} = \frac{1}{4\pi \varepsilon_0} \frac{q_1 q_2}{|\boldsymbol r_1 - \boldsymbol r_2|}
  • Gravitation :
    E_{\rm p} = -\frac{G m_1m_2}{|\boldsymbol r_1 - \boldsymbol r_2|}

Oscillateur

Oscillateur harmonique (sans amortissement)

  • Équation différentielle de la forme :
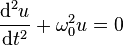
    \frac{\text{d}^2 u}{\text{d} t^2}+\omega_0^2 u=0 .
  • Pulsation propre :
    \omega_0=\frac{k}{m}
  • Période propre:
    T_0=\displaystyle \frac{2\pi}{\omega_0}
  • Solution sous la forme :
    u(t) = Acos(ω0t) + Bsin(ω0t).

Les constantes A et B sont déterminées par les conditions initiales.

Oscillateur avec facteur d'amortissement λ

  • Équation différentielle de la forme :
    \frac{\text{d}^2 u}{\text{d} t^2}+2\lambda\frac{\text{d} u}{\text{d} t}+\omega_0^2 u=0
  • Trois cas selon la valeur du discriminant de l'équation caractéristique :
    \Delta=4(\lambda^2-\omega_0^2)
    • Δ < 0, soit λ < ω0, alors
      (régime pseudo-périodique)
      Pseudo-pulsation :
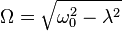
      \Omega=\sqrt{\omega_0^2-\lambda^2}  ;
      Pseudo-période :
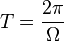
      T=\displaystyle \frac{2\pi}{\Omega}
    • Δ = 0, soit λ = ω0, alors
      x(t) = (At + B)e − λt (régime critique)
    • Δ > 0, soit λ > ω0, alors
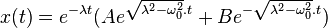
      x(t)=e^{-\lambda t}(Ae^{\sqrt{\lambda^2-\omega_0^2}.t}+Be^{-\sqrt{\lambda^2-\omega_0^2}.t}) (régime apériodique)
  • Dans chaque cas, les constantes A et B sont déterminées par les conditions initiales.
- Introduction - Cinématique : le rayon vecteur et ses dérivées successives - Dynamique - Changement de référentiel - Notion de Moment - Aspect énergétique - Oscillateur
miniature
Des particules de lumière "filmés" dans leur déplacement 🎬
miniature
Montre moi tes mains, je te dirai quel buveur d'alcool tu es 🍺
miniature
Ces papillons interprètent les "cris" des plantes pour choisir où pondre 🦋
miniature
3
Le nombre d'articles scientifiques rétractés est en hausse ❌
miniature
Une nouvelle manière de lire les mémoires magnétiques 🧲
miniature
2
Vous êtes né avant 1986 ? Voici pourquoi vous risquez de développer des troubles psychiques ⚠️
miniature
Ce nouveau modèle relie matière noire et inflation cosmique 🌀
miniature
Ils ont rendu ce bois bioluminescent: vers un nouveau mode d'éclairage ? 💡
miniature
Des mouches dans la station spatiale chinoise Tiangong 🛰️
miniature
Cette main-robot nanométrique est capable de saisir des virus (exemple avec la COVID-19) 🖐️
miniature
1
Une étoile dévorée à pleine vitesse par... un trou noir ? 🌟
miniature
Cette astuce simple réduit la consommation d'alcool... des femmes 🍷
miniature
Découverte: la lumière transforme un isolant en métal 💡
miniature
1
Cet aliment à bannir nourrit les cancers 🍽️
miniature
Cette tablette de 3000 ans dévoile une écriture jusqu'alors inconnue ✍️
miniature
Découverte d'une chimie des océans refroidissant le climat 🌊
miniature
Le télescope James Webb, poussé à ses limites, découvre ces structures incroyablement anciennes 🔭
miniature
Le rôle surprenant de la grossesse contre la grippe A 🦠
miniature
Découverte d'une nouvelle espèce éteinte grâce à... un accélérateur de particules ⚛️
miniature
Une avancée prometteuse pour le déploiement des batteries sodium-ion 🔋
miniature
Voici comment et pourquoi le risque de cancer augmente... puis diminue avec l'âge 🧬
miniature
Le Soleil bientôt en "zone de combat": une période de turbulences extrêmes ☀️
miniature
1
Les rhumatismes plus douloureux par temps humide: vrai ou faux ? 🌧️
miniature
Ce nouveau type de moteur repousse les limites du vol supersonique ✈️
miniature
Poster sur les réseaux sociaux peut nuire à votre santé mentale 🧠
miniature
Une super-Terre entre Mars et Jupiter ? 🌎
miniature
Découverte impressionnante d'un fossile de crocodile géant 🐊
miniature
1
Cet accident en laboratoire pourrait transformer drastiquement la mémoire numérique ⚡
miniature
1
Un virage technologique révèle l'impact du diabète gestationnel 🩺
miniature
Insolite: ces loups butinent des fleurs ! Des grands carnivores pollinisateurs ? 🌼
miniature
1
Ce fin gilet robotisé soulage les tâches répétitives 🦾
miniature
Les équations d'Einstein invalidées ? 👀
miniature
Ce tatouage électronique se connecte à votre cerveau 🧠
miniature
Cette IA de Google prédit la météo mieux que jamais, et sur 15 jours ! 🌦️
miniature
Des plats au bœuf... sans bœuf ? 🥩
miniature
2
Ce moteur de recherche d'un nouveau genre bouscule nos habitudes 🔍
miniature
Pourquoi les cheveux bouclent-ils en fonction de la météo ? 🌦️
miniature
Découverte: d'autres univers plus propices à la vie que le notre 👽
miniature
Ces sons urbains qui minent notre santé mentale 🚗
miniature
La testostérone impacte-t-elle vraiment le désir sexuel des hommes ? 🔥
miniature
Des microalgues éliminent les métaux lourds: voici comment 🧪
miniature
1
Et voici un qubit mécanique ! 🖥️
miniature
Les lentilles de contact sont-elles vraiment sans danger ? 👁️
miniature
Dans la course à l'IA générative, Google lance son générateur de vidéos 🎥
miniature
4
Une zone oubliée du cerveau permet aux paralysés de marcher à nouveau 🧠
miniature
Cette astuce quotidienne ajoute 11 ans à votre vie 🕒
miniature
Révolutions, migrations des européens... les éruptions volcaniques ont influencé l'histoire 🌋
miniature
Soit l'énergie noire n'est pas constante, soit une seconde force inconnue est à l'œuvre... 🌀
miniature
Voici pourquoi l'alcool peut rendre agressif 🥂
miniature
Expérience inédite: ce laser projette une ombre visible 💥
Page générée en 0.194 seconde(s) - site hébergé chez Contabo
Ce site fait l'objet d'une déclaration à la CNIL sous le numéro de dossier 1037632
A propos - Informations légales | Partenaire: HD-Numérique
Version anglaise | Version allemande | Version espagnole | Version portugaise