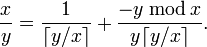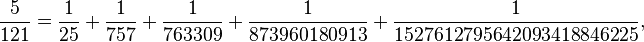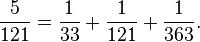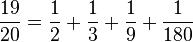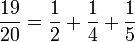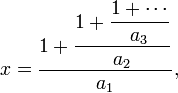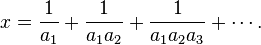Fraction égyptienne - Définition

Mathématiques médiévales

La notation sous forme de fractions égyptiennes a été utilisée pendant la période grecque et même au Moyen Âge (Struik 1967) en dépit des plaintes dès l'Almageste de Ptolémée à propos de la maladresse de cette notation comparée aux notations alternatives telles que la notation babylonienne en base soixante.

Le Liber Abaci (1202) de Fibonacci contient plusieurs sections sur les mathématiques liées aux fractions égyptiennes. La plus connue de ces dernières est l'algorithme glouton pour le calcul des fractions égyptiennes, par le choix répété de la fraction unitaire avec le plus petit dénominateur qui n'est pas plus grand que la fraction restante à développer : c’est-à-dire, dans une notation plus moderne, nous remplaçons une fraction x//y par le développement :

Comme chacun de ces développements réduit le numérateur de la fraction restante à développer, cette méthode termine toujours avec un développement fini ; néanmoins, comparée aux développements égyptiens anciens ou aux méthodes plus modernes, cette méthode peut produire des développements qui sont longs, avec de grands dénominateurs. Par exemple, cette méthode développe :

tandis que d'autres méthodes conduisent au meilleur développement :

La suite de Sylvester 2, 3, 7, 43, 1807, ... peut être vue comme engendrée par un développement glouton infini de ce type pour le nombre un, où à chaque étape, nous choisissons le dénominateur : à la place de

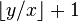
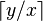
Construire une représentation par fraction égyptienne d'un nombre rationnel donné r=a/b, avec r compris entre 0 et 1 :

1. Trouver la plus grande fraction unitaire juste inférieure à r. Le dénominateur peut être trouvé en divisant b par a, en écartant le reste, et en additionnant un. S'il n'y a pas de reste, nous réussissons quand même, car r est elle-même une fraction unitaire.
2. Soustraire la fraction unitaire trouvée de r, puis recommencer l'étape précédente en utilisant cette valeur plus petite que r.

Exemple : convertir 19/20 en une fraction égyptienne.

• 20/19 = 1 avec un certain reste, donc notre première fraction unitaire est 1/2.
• 19/20 - 1/2 = 9/20.
• 20/9 = 2 avec un certain reste, donc notre deuxième fraction unitaire est 1/3.
• 9/20 - 1/3 = 7/60
• 60/7 = 8 avec un certain reste, donc notre troisième fraction unitaire est 1/9.
• 7/60 - 1/9 = 1/180 qui est elle-même une fraction unitaire.

Donc, notre résultat est :

Notez que cette représentation d'un nombre rationnel donné sous forme de fraction égyptienne n'est pas unique, et que l'algorithme donné plus haut ne produit pas la plus petite de ces représentations :

Quelquefois, l'algorithme glouton de Fibonacci est attribué à Sylvester.

Dans le Liber Abaci, Fibonacci a écrit aussi à propos de la forme ascendante d'une fraction continue,

qui peut être réécrite comme une sorte de fraction égyptienne, quelquefois appelée un produit égyptien :

Un développement de cette forme dans lequel les entiers a_i sont croissants est appelé un développement d'Engel. Chaque nombre rationnel possède un développement d'Engel fini, tandis que les nombres irrationnels ont un développement d'Engel infini.

Conjecture de Sierpiński

Pour tout entier n > 1, il existe trois naturels a, b et c tels que :

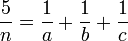
Remarque : contrairement aux fractions égyptiennes, on n'impose pas à a, b et c d'être tous différents.

Il semble que l'on ne sache pas encore démontrer la conjecture de Wacław Sierpiński.

	Histoire • Géographie • Mythologie • Dieux • Art / Pyramides • Sciences • Vie quotidienne / Organisation politique / Pharaons		Égyptologie • Bibliographie • Lexique • Index
Egyptopedia	Un article égyptologique au hasard :	Ouni	Modifications du jour