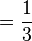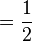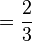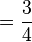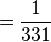Fraction égyptienne - Définition
La liste des auteurs de cet article est disponible ici.
Introduction

|
| Mathématiques |
| Médecine |
| Astronomie |
Une fraction égyptienne est une somme de fractions unitaires, c'est-à-dire de fractions qui ont des numérateurs égaux à 1 et des dénominateurs entiers positifs, avec ces dénominateurs tous différents les uns des autres.
Il peut être montré que tous les nombres rationnels positifs peuvent être écrits sous cette forme et ce, d'une infinité de façons différentes.
En effet, il est trivial d'exprimer toutes fractions par une somme de fractions unitaires en se permettant de répéter les termes comme dans l'exemple :
-
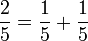
Mais si l'on exige que tous les dénominateurs soient distincts, à l'instar des Égyptiens durant l'antiquité, cette représentation est toujours possible grâce à l'identité :
-
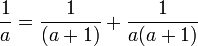
Ainsi, en reprenant l'exemple ci-dessus : 2/5 = 1/5 + 1/6 + 1/30. En appliquant le même procédé à chacune des fractions unitaires, 2/5 peut donc s'exprimer comme une multitude de fractions égyptiennes.
On peut démontrer le même résultat en utilisant les séries harmoniques.
Il peut être montré que chaque nombre rationnel positif, a/b, peut être écrit sous la forme d'une fraction égyptienne. Ce type de sommes, utilisé pour exprimer les fractions par les anciens Égyptiens, a continué à faire l'objet d'études lors de la période médiévale. En notation mathématique moderne, les fractions égyptiennes ont été remplacées par les fractions vulgaires et la notation décimale. Néanmoins, les fractions égyptiennes continuent d'être un objet d'étude en théorie des nombres moderne et en mathématiques récréatives, aussi bien que dans les études historiques modernes des mathématiques anciennes.
Dans cet article, nous résumons ce qui est connu à propos des fractions égyptiennes à la fois anciennes et modernes. Pour les détails des sujets traités ici, voir les articles liés.
Les fractions dans l'Égypte antique
Cette propriété a permis aux anciens Égyptiens d'exprimer simplement tous les nombres rationnels.
N'importe quelle fraction que nous écrivons avec un numérateur non unitaire était écrite par les anciens Égyptiens comme une somme de fractions unitaires sans que deux de ces dénominateurs soient les mêmes.
Le hiéroglyphe en forme de bouche ouverte qui signifie partie était utilisé pour représenter le numérateur 1 :
|
Les fractions étaient écrites avec ce hiéroglyphe dessus et le dénominateur en dessous. Ainsi 1/3 était écrit :
|
|
Il y avait des symboles spéciaux pour les fractions les plus courantes comme 1/2 et pour deux fractions non unitaire 2/3 et 3/4 :
|
|
|
|
|
|
Si le dénominateur devenait trop large, la "bouche" était placée juste au début du dénominateur :
|
|
Bien que d'usage peu commode, la représentation d'un nombre rationnel en fractions égyptiennes comme se l'imposaient les Égyptiens permet de déterminer immédiatement qu'une fraction est plus grande que l'autre.
Exemple :
- 55/84 = 1/2 + 1/7 + 1/84
- 7/11 = 1/2 + 1/8 + 1/88
Donc, le nombre rationnel 55/84 est clairement plus grand que 7/11 alors que ces deux nombres ne diffèrent entre eux que de 2% environ.
La "table de deux" du Papyrus Rhind
Le papyrus Rhind (environ -1650) qui est conservé au British Museum de Londres, est le plus important document nous informant des connaissances mathématiques des temps anciens. Il comporte 87 problèmes résolus d'arithmétique, d'algèbre, de géométrie et d'arpentage. Mais, avant de prendre connaissance de ces problèmes, l'égyptien devait avoir à sa disposition différentes tables lui permettant de décomposer directement les fractions non unitaires en fractions unitaires. Une de ces tables, la table dite "de deux", se trouve en première position sur le Papyrus de Rhind. Elle répertorie les fractions dont le numérateur est 2 et dont le dénominateur varie de 3 à 101, et donne leur équivalent en somme de fractions unitaires.
Quelques exemples de décomposition en fractions unitaires de la table de deux :
| 2/5 | -> 1/3 + 1/15 | |
| 2/7 | -> 1/4 + 1/28 | |
| 2/9 | -> 1/6 + 1/18 | |
| 2/11 | -> 1/6 + 1/66 | |
| 2/101 | -> 1/101 + 1/202 + 1/303 + 1/606 |
Ces différents résultats furent obtenus par les anciens égyptiens en appliquant la technique de la division :
exemple de 2/5 :
| 1 | 5 | |
| 2/3 | 3 + 1/3 | |
| ✔ | 1/3 | 1 + 2/3 |
| ✔ | 1/15 | 1/3 |
| | ||
| 1/3 + 1/15 | 2 | |
(1 + 2/3) + 1/3 = 2 par conséquent le résultat est 1/3 + 1/15.
Exemple du papyrus Rhind
Le problème numéro 24 du papyrus est le suivant : Un nombre ajouté à son septième donne 19, quel est ce nombre ?
Sous forme symbolique moderne, la réponse est triviale: x + x/7 = 8x/7 = 19, soit x = 133/8.
Mais il y a 4 000 ans, le calcul fractionnaire et le symbolisme algébrique n'étaient pas vraiment au point. En fait, le problème n'est alors pas dans la résolution même de l'équation, mais dans la mise en équation et la difficulté d'aboutir, à défaut d'une démarche algébrique pratique, à la forme simple ax = b.
Pour cela les Égyptiens utilisaient la méthode dite de la fausse position. On appelle ainsi une méthode de résolution algébrique consistant à fournir une solution approchée (fausse) conduisant, par un algorithme approprié tirant parti de l'écart constaté, à la solution du problème considéré.
Dans notre exemple l'idée première est de se débarrasser du dénominateur gênant en choisissant 7 comme solution "approchée" (fausse position) : le scribe obtient 8 dans le calcul du nombre augmenté de son septième. Il utilise ensuite implicitement l'algorithme suivant (où x' = 7 et c = 8) :
Si ax = b et ax'= c alors ax/ax' = b/c soit x = x'(b/c)
C'est exactement ce qui est proposé dans le papyrus : on divise 19 par 8, ce qui fournit 2 + 1/4 + 1/8 et multiplie le tout par 7 = 1 + 2 + 4, ce qui fournit (2 + 1/4 + 1/8) + (4 + 1/2 + 1/4) + (9 + 1/2), soit 16 + 1/2 + 1/8.