Gottfried Wilhelm Leibniz - Définition

Mathématiques

Les travaux mathématiques de Leibniz se trouvent dans le Journal des savants de Paris, les Acta Eruditorum de Leipzig (qu’il a contribué à fonder) ainsi que dans son abondante correspondance avec Huygens, les frères Bernoulli, l’Hospital, Varignon, etc.

Le « nouveau calcul »

L’algorithme différentio-intégral achève une recherche débutée avec la codification de l’algèbre par Viète et l’algébrisation de la géométrie par Descartes. Tout le XVII^e siècle étudie l’indivisible et l’infiniment petit. Comme Newton, Leibniz domine tôt les indéterminations dans le calcul des dérivées. De plus il développe un algorithme qui est l’outil majeur pour l’analyse d’un tout et de ses parties, fondé sur l’idée que toute chose intègre des petits éléments dont les variations concourent à l’unité. Ses travaux sur ce qu’il appelait la « spécieuse supérieure » seront poursuivis par les frères Bernoulli, le marquis de l’Hospital, Euler et Lagrange.

Notation de Leibniz

Leibniz développe une symbolique mathématique qu’il tente d’intégrer dans une notion plus générale qu’il appelle sa caractéristique universelle qu’il voulait pouvoir appliquer à tous les domaines.

Il est à l’origine du terme de « fonction » (1692, de functio : exécution), de celui de « coordonnées », de la notation du produit de a par b sous la forme a.b ou ab, d’une définition logique de l’égalité, du terme de « différentielle » (qu’Isaac Newton appelle « fluxion »), de la notation différentielle , du symbole pour l’intégrale.

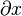
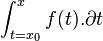
Calcul infinitésimal : Newton ou Leibniz ?

Dans l’histoire du calcul infinitésimal, le procès de Newton contre Leibniz est resté célèbre. Newton et Leibniz avaient trouvé l’art de lever les indéterminations dans le calcul des tangentes ou dérivées. Mais Newton a publié tard (son procès intervient en 1713, presque 30 ans après les publications de Leibniz: 1684 et 1686) et, surtout, Newton n’a ni l’algorithme différentio-intégral fondé sur l’idée que les choses sont constituées de petits éléments, ni l’approche arithmétique nécessaire à des différentielles conçues comme « petites différences finies ».

Autres travaux

Leibniz s’intéresse aux systèmes d’équations et pressent l’usage des déterminants. Dans son traité sur l’art combinatoire, science générale de la forme et des formules, il développe des techniques de substitution pour la résolution d’équation. Il travaille sur la convergence des séries, le développement en série entière des fonctions comme l’exponentielle, le logarithme, les fonctions trigonométriques (1673). Il découvre la courbe brachistochrone et s’intéresse à la rectification des courbes (calcul de leur longueur). Il a étudié le traité des coniques de Pascal et écrit sur le sujet. Il est le premier à créer la fonction (conspectus calculi). Il étudie les enveloppes de courbes et la recherche d’extremum pour une fonction (Nova methodus pro maximis et minimis 1684). Il conçoit une machine arithmétique inspirée de la Pascaline. Il tente aussi une incursion dans la théorie des graphes et la topologie (analysis situs).

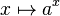
Pour l’anecdote, on trouve dans le Compte Rendu de l’Académie des Sciences (Paris, 1703, p. 85-89 des Mémoires) un article de Leibniz intitulé Explication de l’arithmétique binaire, qui se sert des seuls caractères 0 & 1, (…). Reconnaissant cette manière de représenter les nombres comme étant un héritage très lointain du fondateur de l’Empire Chinois « Fohy », Leibniz s’interroge longuement sur l’utilité des concepts qu’il vient de présenter, notamment en ce qui concerne les règles arithmétiques qu’il développe. Finalement il semble conclure que la seule utilité qu’il voit dans tout ceci est une sorte de beauté essentielle, qui révèle la nature intrinsèque des nombres et de leurs liens mutuels. C’est un quart de millénaire avant l’apparition de l’informatique…