Groupe abélien de type fini - Définition
La liste des auteurs de cet article est disponible ici.
Cas des groupes finis
Si G est d'ordre fini, il dispose alors d'une décomposition particulièrement simple:
-
- Il existe une suite d'entiers strictement positifs (a1,a2,...,ak) tel que G est isomorphe au produit direct des groupes cycliques de cardinal les différents éléments de la suite. De plus il est possible de choisir la suite tel que ai+1 divise ai si i est un entier entre 1 et k - 1.
Il existe donc la suite suivante isomorphe au groupe G:
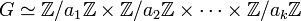
Ce théorème est connu sous le nom de théorème de Kronecker, la démonstration est donnée dans l'article détaillé.
Relation avec les modules
Soit g un élément de G et n un entier positif. L'expression n.g possède un sens. En effet, elle désigne l'élément de G obtenu par l'addition n fois de g. De même l'expression -n.g signifie l'inverse de n.g ou n fois l'addition de l'opposé de g.
Ces remarques permettent de conclure que Z opère sur le groupe. Il est aisé de vérifier que les axiomes définissant la structure de module sont vérifiés. En conclusion tout groupe abélien de type fini dispose d'une structure naturelle de Z module.
Cette notion permet d'identifier un groupe abélien de type fini avec un Z module. La théorie devient alors analogue à celle des espaces vectoriels. Il est possible de parler de famille génératrice, de famille libre et donc de base. En revanche, le théorème du rang ne s'applique pas. En effet, sur Z/6 Z, la classe de 1 est une génératrice et aucune sous-famille ne l'est, il en est de même de la famille constituée des classes de 2 et 3. Il existe donc deux familles génératrices minimales n'ayant pas le même cardinal.
Un morphisme de groupe est aussi un morphisme de module.
Cas général
Module libre
Un groupe abélien fini considéré comme un Z module ne peut contenir de base. En effet, toute combinaison linéaire de coefficient l'exposant du groupe pour chaque élément d'une famille du groupe est égale à l'élément neutre. Il en va différemment pour les groupes libres.
-
- Un groupe abélien de type fini est libre si et seulement s'il existe une base du groupe considéré comme un Z module.
On remarque alors que la donnée d'une base fournit directement un isomorphisme entre le groupe et une puissance de Z.
Dans le cas d'un groupe libre de type fini, alors le théorème définissant la dimension, analogue à celui de l'algèbre linéaire s'applique encore:
-
- Les bases d'un groupe abélien de type fini libre ont toutes le même cardinal.
Ce qui implique que si n est un entier différent d'un autre entier m, alors il n'existe aucun isomorphisme entre Z n et Z m. La situation, dans le cas des groupes libres est alors analogue à celle des espaces vectoriels.
La théorie des matrices donne alors une condition nécessaire et suffisante pour qu'une famille soit une base :
-
- Soit B une base d'un groupe G libre de type fini. Une famille F est une base si et seulement si la matrice de passage de B dans F possède un déterminant égal à 1 ou -1.
Certaines autres propriétés analogues aux espaces vectoriels s'appliquent encore:
-
- Tout sous-groupe d'un groupe abélien libre de type fini est un sous-groupe abélien libre de type fini.
-
- Tout produit direct fini de groupes abéliens libres de type fini est un groupe abélien libre de type fini.
Les démonstrations proposées ici se fondent essentiellement sur la structure de Z module du groupe.
-
- Si G, un groupe libre de type fini, possède une base alors son cardinal est fini et toute base de G possède le même cardinal.
Soit (ei) une base de G et (gj) une famille génératrice finie. Chaque élément gj est engendré par une partie finie de la base, et la famille génératrice finie est engendré par une partie finie de la base. Ceci démontre que la base est de cardinal fini.
Considérons alors l'application canonique ψ de G dans G/2G, l'ensemble d'arrivée peut être muni d'une structure de F2 espace vectoriel où F2 désigne le corps à deux éléments.
Montrons que (ψ(ei)) est une base de G/2G. La famille est génératrice car (ei) est une base et ψ est un morphisme de groupe surjectif.
Montrons alors que la famille est libre. Soit β1.ψ(e1) + ...+ βk.ψ(ek) une combinaison linéaire nulle de la famille (ψ(ei)) et α1.e1 + ...+ αk.ek un antécédent par ψ de cette combinaison linéaire. Comme l'antécédent est élément de 2G, chaque αi est paire, ce qui démontre que chaque βi est nul. La famille est bien libre.
En conclusion, à toute base de G est associé une base d'un F2 espace vectoriel. Or toute base d'un même espace vectoriel possède le même cardinal. Toute base de G possède donc bien le même cardinal.
-
- Soit B une base de G, B' est une base de G un groupe libre de type fini, si et seulement si l'endomorphisme qui a pour image de la base B, B' est un isomorphisme. Ou encore B' est une base si et seulement si la matrice de transfert de la base B vers la base B' possède un déterminant égal à 1 ou à -1.
Si φ est un isomorphisme, alors la base B' engendre par combinaison linéaire la base B et donc le groupe G tout entier. L'unique combinaison linéaire nulle de la base B est la combinaison linéaire à coefficients nuls. L'application de l'isomorphisme φ montre que l'unique combinaison linéaire nulle de B' est aussi la combinaison linéaire à coefficients nuls.
Réciproquement si B' est une base de G, alors l'application qui associe B à B' est surjectif car B' engendre G et possède pour noyau {0} car l'unique combinaison linéaire de B' nulle est la combinaison linéaire à coefficients nuls.
Si la matrice M de transfert de B dans B' possède un déterminant inversible, alors si cM désigne la comatrice de M, l'égalité cM.M = det(M) montre le caractère inversible de l'endomorphisme de passage de la base B à la base B '. Réciproquement si l'endomorphisme de transfert de B dans B' est inversible, alors la matrice M-1 vérifie: det(M).det(M-1) = 1 ce qui montre que det(M) est inversible. La conclusion provient du fait qu'il n'existe que deux éléments inversibles dans Z: 1 et -1.
-
- Soit n un entier strictement positif et (λ1, λ2, ..., λn) les coordonnées d'un élément e1 de G dans une base B. Alors e1 peut être complété en une base (e1, e2, ..., en) si et seulement si la famille des (λ1, λ2, ..., λn) ne contient que des éléments premiers dans leur ensemble.
Démontrons dans un premier temps, que la condition est nécessaire:
Si (λ1, λ2, ..., λn) n'est pas une famille de nombres premiers entre eux dans leur ensemble, alors il existe un entier l strictement supérieur à 1 et un élément z de Z n tel que e1 = l. z. Soit (e1, e2, ..., en) une famille génératrice de G. Alors l. z possède au moins deux combinaisons linaires distinctes : d'une part l fois la combinaison linéaire de z et d'autre part e1. La famille ne peut donc être une base de G.
Démontrons alors la réciproque par une récurrence sur n:
Si n est égal à 2: alors l' identité de Bézout montre l'existence de deux entiers p et q tel que : λ1.p + λ2.q = 1. Soit e2 l'élément de coordonnées (-p,q). L'endomorphisme qui à la base B associe la famille (e1, e2) possède un déterminant égal à 1. La proposition précédente permet de conclure.
Supposons le résultat vrai pour tout groupe ayant une base à n - 1 éléments. Considérons un groupe abélien de type fini ayant une base à n éléments. Soit B une base et G' le groupe engendré par la famille B' des n-1 premiers éléments de B. B' est clairement une base de G'. Soit (λ1, λ2, ..., λn) une famille d'entiers premiers entre eux dans leur ensemble et soit a le pgcd de la famille (λ1, λ2, ..., λn-1). On définit μi par l'égalité a.μi = λi où i est un entier compris entre 1 et n - 1.
L'hypothèse de récurrence montre qu'il existe une famille de coefficients (cij) tel que le déterminant suivant est égal à une unité de Z que l'on peut choisir comme valant 1:
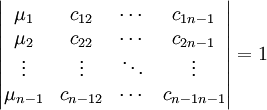
les deux entiers a et λn sont premier entre eux, il existe donc deux entiers p et q tel que la somme p.a + q.λn soit égale à 1. Cette égalité montre que le déterminant suivant est égal à 1.
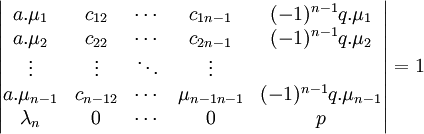
La première colonne correspond aux coefficients de la famille (λ1, λ2, ..., λn). On en conclut que le déterminant correspond à une matrice de passage d'un endomorphisme inversible sur la structure de Z module, e1 est donc bien le premier vecteur d'une base de G.
Nous disposons maintenant d'une méthode puissante pour construire des bases de groupes libres de type fini, à la condition qu'au moins une base existe. C'est le cas sur Z n, mais c'est aussi le cas pour tout quotient libre de Z n.
-
- Soit n un entier strictement positif et K un sous-groupe de Z n tel que le quotient Z n/K soit sans torsion. Alors il existe un entier positif m tel que Z n/K est isomorphe à Z m.
Démontrons ce résultat par récurrence sur n:
Si n est égal à 1, le seul quotient qui soit un groupe libre est obtenu avec le sous-groupe {0}. La proposition est donc vérifiée.
Supposons la proposition vraie à l'ordre n - 1. Soit K un sous-groupe de Z n tel que le quotient soit libre. Si K est réduit à l'élément neutre, alors la proposition est évidente. Dans le cas contraire, soit f un élément de K non nul. Soit a le pgcd des coefficients de f et soit f = a.en, le morphisme canonique φ vérifie φ(f)=a.φ(en) qui est égal à 0. La classe de en n'est pas un élément de torsion et a.φ(en) est égal à 0 donc en est élément du noyau de φ.
L'élément en est élément d'une base de Z n d'après la proposition précédente. Soit (e1, e2, ...,en) une telle base. L'image de φ est égale à l'image du groupe G' engendré par les n -1 premiers vecteurs de la base. G' possède une base de cardinal n - 1 donc est isomorphe à Z n-1. Donc l'image de φ est isomorphe à un quotient de Z n-1 par un groupe tel que le quotient est un groupe libre. L'hypothèse de récurrence permet alors de conclure.
-
- Pour tout groupe libre de type fini G il existe un entier n tel que le groupe soit isomorphe à Z n.
Soit une famille génératrice (e1, e2, ...,em) de G. Considérons le morphisme φ de Z m dans G définit par:
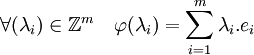
Le morphisme φ est par construction surjectif. Le théorème fondamental des morphismes montre alors que G est isomorphe au quotient de Z m par le noyau de φ. Ce quotient est un groupe libre, la proposition précédente montre qu'il existe n tel que ce quotient et donc G est isomorphe à Z n.
-
- Tout groupe libre de type fini G admet au moins une base et toutes ses bases contiennent le même nombre d'éléments.
Il existe n un entier strictement positif tel que G soit isomorphe à Z n. Z n admet une base de cardinal fini donc G admet une base de cardinal fini. Or il a été démontré que s'il existe une base dans un groupe libre de type fini toutes les bases possèdent le même cardinal, ce qui termine la démonstration.
-
- Tout sous-groupe d'un groupe abélien libre de type fini est un sous-groupe abélien libre de type fini.
Le caractère abélien et libre d'un sous-groupe est évident. Pour montrer qu'un sous-groupe d'un groupe abélien libre de type fini est de type fini, raisonnons par la contraposée. Soit G un groupe abélien libre et H un sous-groupe qui n'est pas de type fini. Montrons par récurrence que, pour tout entier positif n, il existe une famille libre de ce cardinal. Si n est égal à 1, il suffit de considérer un élément non nul. Si la propriété est vraie à l'ordre n, il existe une famille libre d'ordre n et qui n'est pas génératrice car H n'est pas de type fini. Il est donc possible d'adjoindre un élément à cette famille non engendré par elle. L'adjonction de cet élément à la famille fournit une famille libre d'ordre n + 1. Le groupe G contient donc une famille libre de cardinal quelconque, il ne contient donc pas de base de cardinal fini et G n'est pas de type fini, ce qui termine la démonstration.
-
- Tout produit direct fini de groupes abéliens libres de type fini est un groupe abélien libre de type fini.
Théorème général
La configuration générale est, là encore, relativement simple. Elle correspond à une adjonction directe des deux cas précédents. Un groupe abélien de type fini est somme directe de son sous-groupe de torsion et un sous-groupe supplémentaire libre.
-
- G est la somme directe d'un sous-groupe libre Ll et d'une famille finie de sous-groupes cycliques Ci où i est un entier compris entre 1 et k. Le cardinal de Ci divise celui de Ci+1 si i est un entier compris entre 1 et k - 1.
G s'écrit donc de la manière suivante :
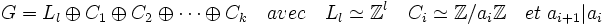
Dans le cas où il existe des éléments de torsion, alors il n'existe plus de base. En effet, toute combinaison linéaire d'un élément de torsion non nul, multiplié par l'ordre de la torsion fournit une combinaison linéaire de valeur nulle à coefficients non tous nuls.
Une conséquence directe du théorème est la stabilité des groupes abéliens de type fini par produit direct fini:
-
- Le produit direct fini de groupes abéliens de type fini est un groupe abélien de type fini.
Le passage au quotient conserve le caractère abélien et de type fini, en effet le morphisme canonique démontre le caractère abélien du groupe quotient car il est surjectif et l'image par ce morphisme d'une famille génératrice est génératrice:
-
- Le quotient d'un groupe abélien de type fini est abélien de type fini.
Le raisonnement développé pour les sous-groupes de groupes abéliens libres de type fini s'applique sans modification, en conséquence :
-
- Tout sous-groupe d'un groupe abélien de type fini est abélien de type fini.
Si le groupe de torsion de G est réduit à l'élément neutre, alors G est un groupe libre de type fini et le paragraphe précédent permet de conclure. Dans le cas contraire, si g1 est un élément de torsion ayant pour ordre l'exposant du groupe de torsion, alors les démonstrations du cas des groupes abéliens finis montrent qu'il existe une somme directe de G en un groupe cyclique engendré par g1 et un complémentaire H.

Une récurrence analogue à celle du cas fini montre qu'il est possible d'appliquer le même raisonnement sur H jusqu'à ce que le supplémentaire ne contienne plus d'élément de torsion.
G est donc somme directe d'un groupe de torsion et d'un groupe de type fini libre. L'analyse des deux situations permet alors de conclure.