Polytope régulier - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
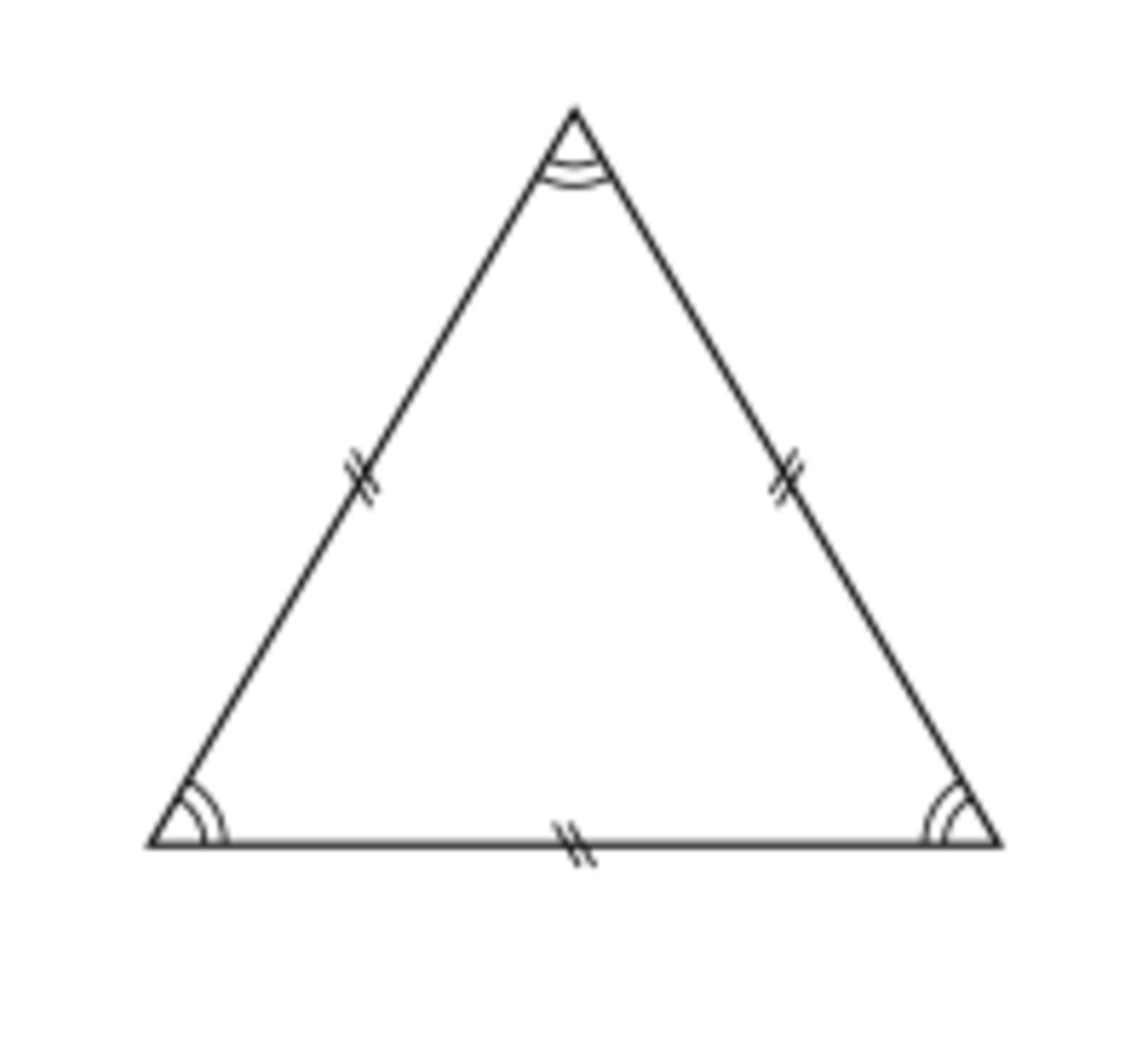
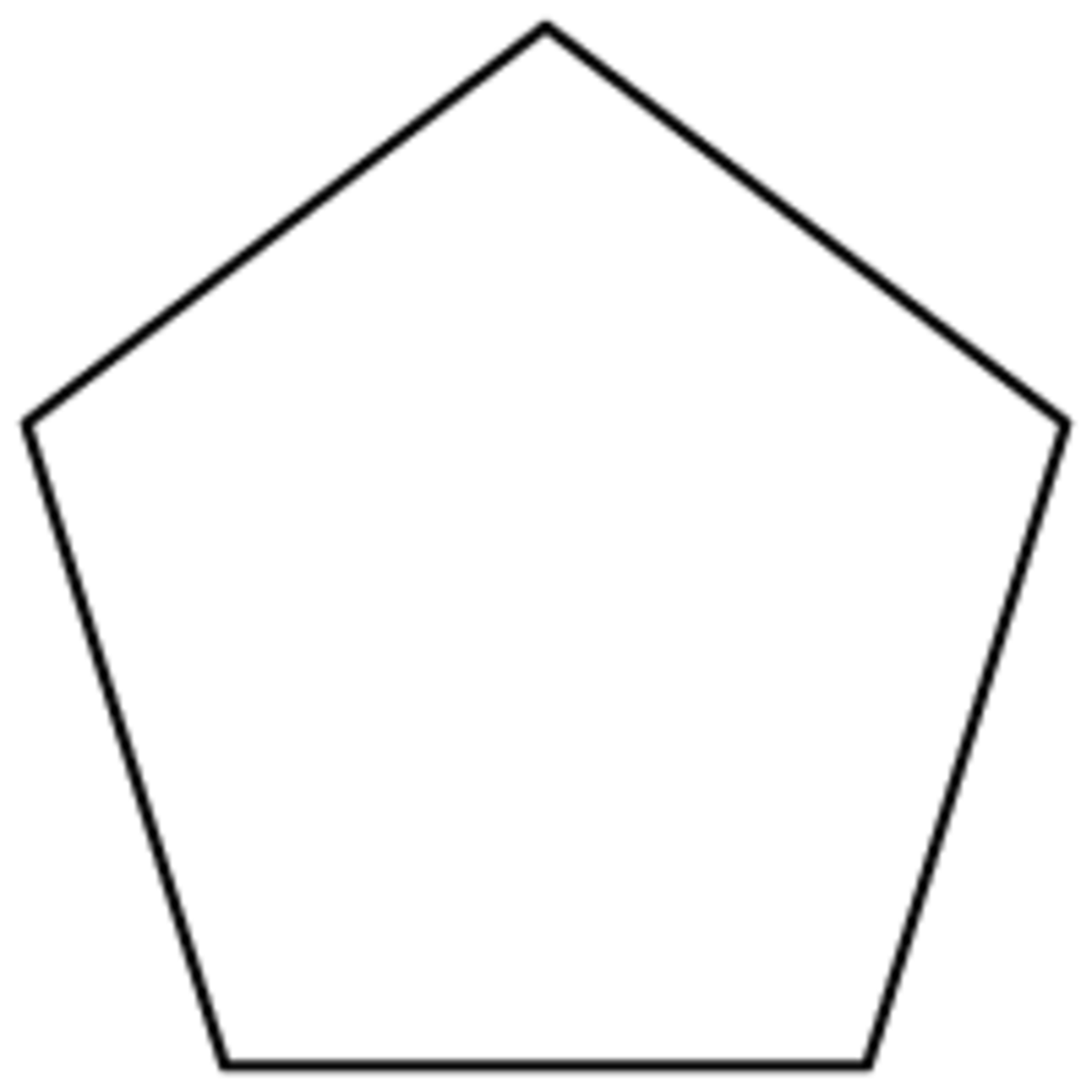
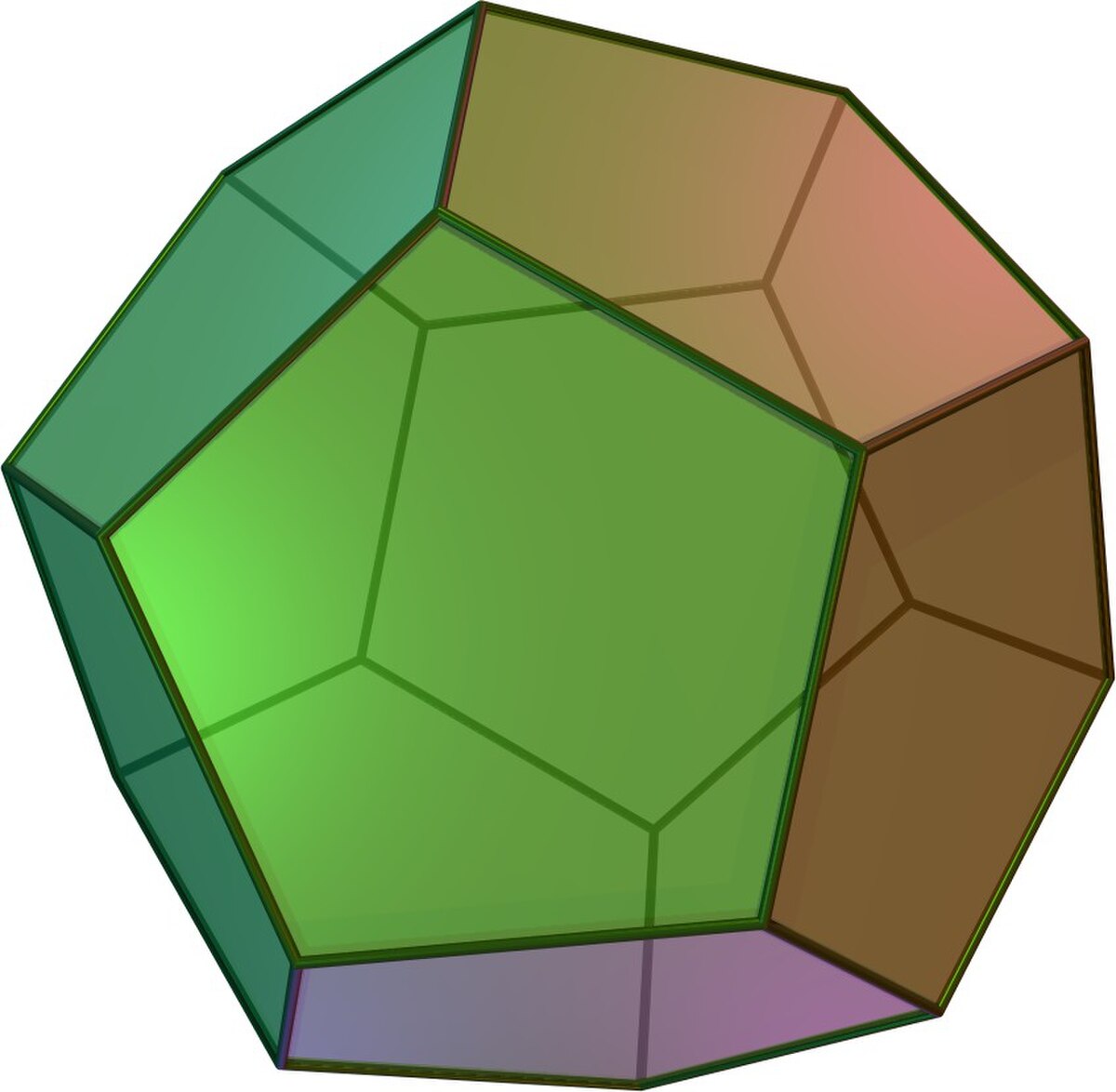
En mathématiques, plus précisément en géométrie ou encore en géométrie euclidienne, un polytope régulier est une figure de géométrie présentant un grand nombre de symétries. En dimension deux, on trouve par exemple le triangle équilatéral, le carré, les pentagone et hexagone réguliers, etc. En dimension trois se rangent parmi les polytopes réguliers le cube, le dodécaèdre (ci-contre), tous les solides platoniciens. On pourrait également citer des exemples pour des espaces de dimension plus élevée. Le cercle et la sphère, qui présentent un degré de symétrie très élevé, n'en sont pas pour autant considérées comme des polytopes, car ils n'ont pas de face plate. La très forte propriété de symétrie des polytopes réguliers leur confère une valeur esthétique qui fascine tant les mathématiciens que les non mathématiciens.
Plusieurs des polytopes réguliers de dimension deux et trois se rencontrent dans la nature et sont connus depuis la Préhistoire. C'est aux mathématiciens grecs de l'Antiquité, notamment Euclide, qu'on en doit le plus ancien traitement mathématique connu. En effet, Euclide rédigea une somme sur les connaissances mathématiques de son temps, qu'il publia sous le titre des Éléments. Ce travail présente une construction d'une géométrie cohérente et d'une théorie des nombres, et se conclut par la description mathématique des cinq solides platoniciens.
De nombreux siècles après Euclide, la définition des polytopes réguliers était demeurée inchangée. Pourtant, cette définition sera ensuite progressivement élargie, par à-coups, de façon à englober de plus en plus d'objets nouveaux. Au milieu du deuxième millénaire, les cinq solides platoniciens originaux furent rejoints par les polyèdres de Kepler-Poinsot. À la fin du XIXe siècle, les mathématiciens commencèrent à prendre en compte des polytopes réguliers en dimension quatre et plus, ainsi l'hypercube, le polytope à 24 cellules. Ces derniers ne sont pas faciles à visualiser, mais partagent avec leurs cousins de petite dimension les mêmes propriétés de symétrie. Plus durs à concevoir encore sont les polytopes réguliers abstraits, tels le polytope à 57 cellules ou celui à 11 cellules. Les mathématiciens qui s'intéressent à ces objets persistent cependant à y retrouver les mêmes qualités esthétiques.
Zoologie des polytopes réguliers
Polygones
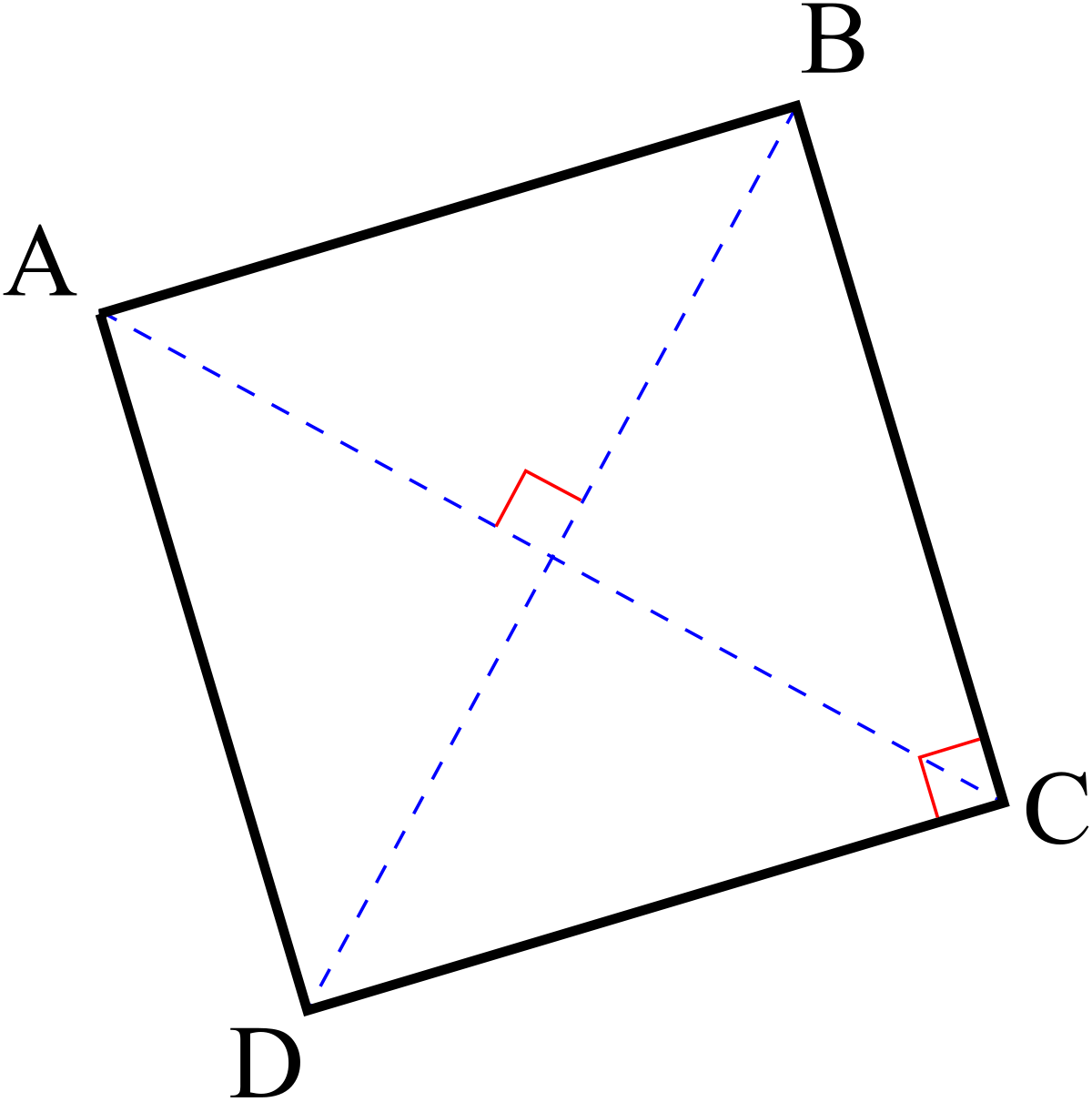
Un polygone régulier à n sommets du plan euclidien R² est la donnée de n points distincts A1, ..., A n , tels que les distances successives A1A2, ..., An-1An et AnA1 soient égales, et les angles au sommets A1, A2, A3 soient égaux. Pour tout entier n supérieur à 3, il existe un polygone régulier à n sommets. Il est unique à similitude près.
La façon traditionnelle de construire un polygone régulier - ou d'ailleurs de construire n'importe quelle figure du plan euclidien - est d'utiliser une règle (non graduée) et un compas. La construction des premiers polygones réguliers (le triangle équilatéral et le carré) est très facile, des suivants plus compliquée, et pour d'autres, elle est impossible ! Cette étude relève des problèmes des points constructibles à la règle et au compas.
En 1796, Carl Friedrich Gauss démontra qu'un polygone régulier à n côtés était constructible à la règle et au compas lorsque les facteurs premiers impairs de n sont des nombres de Fermat distincts. Gauss conjectura que cette condition était de plus nécessaire, conjecture qui fut démontrée par Pierre Wantzel quarante ans plus tard, en 1837. Évidemment, ici la constructibilité fait référence à une construction idéale avec des outils idéaux. L'imperfection inhérente des compas et règles utilisées en pratique nous autorisent des constructions approchées. Quand bien même il n'est pas possible de construire un polygone régulier à 7 côtés, il est possible de réaliser un polygone à 7 côtés qui s'en rapproche.
Polyèdre
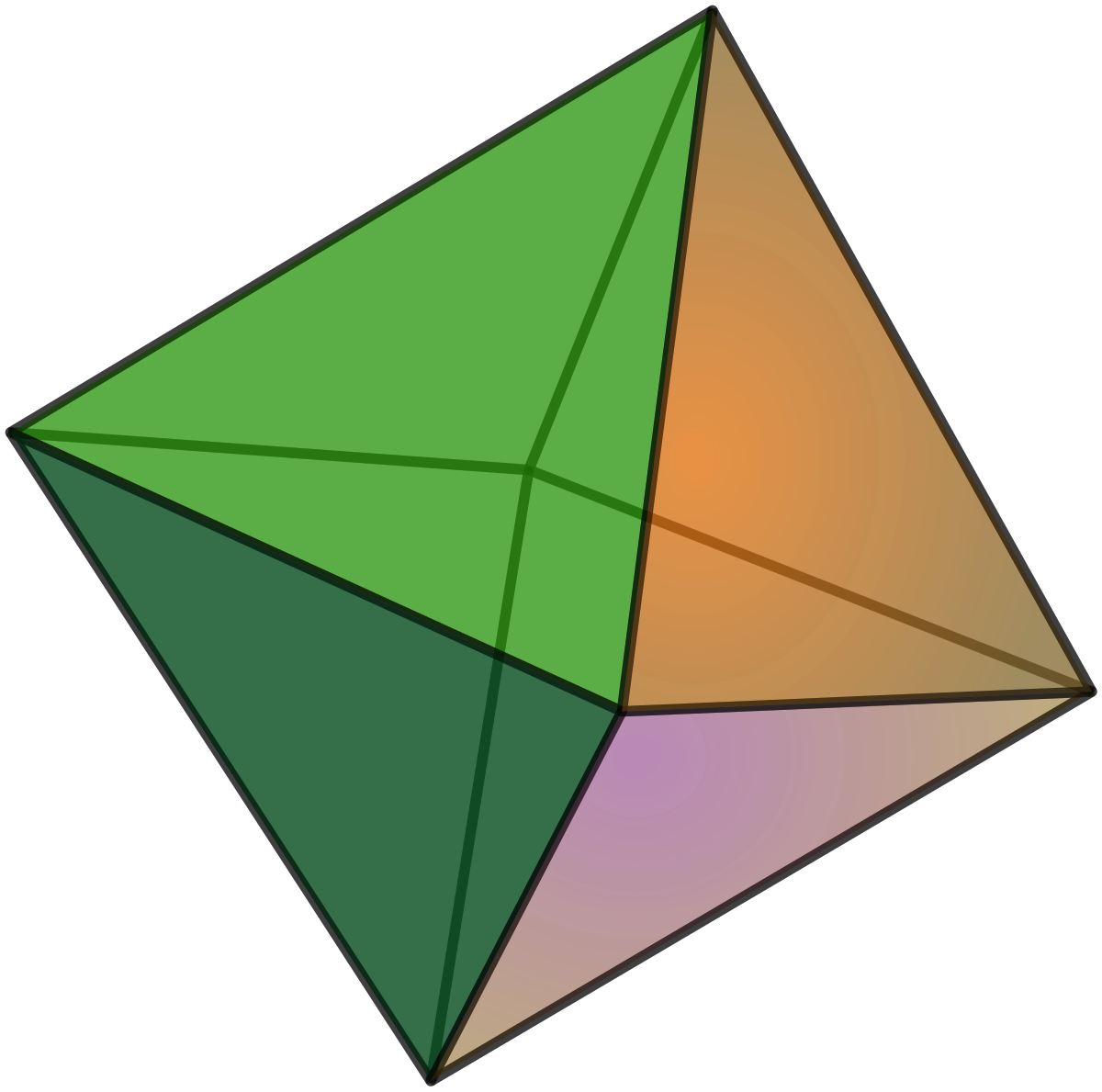
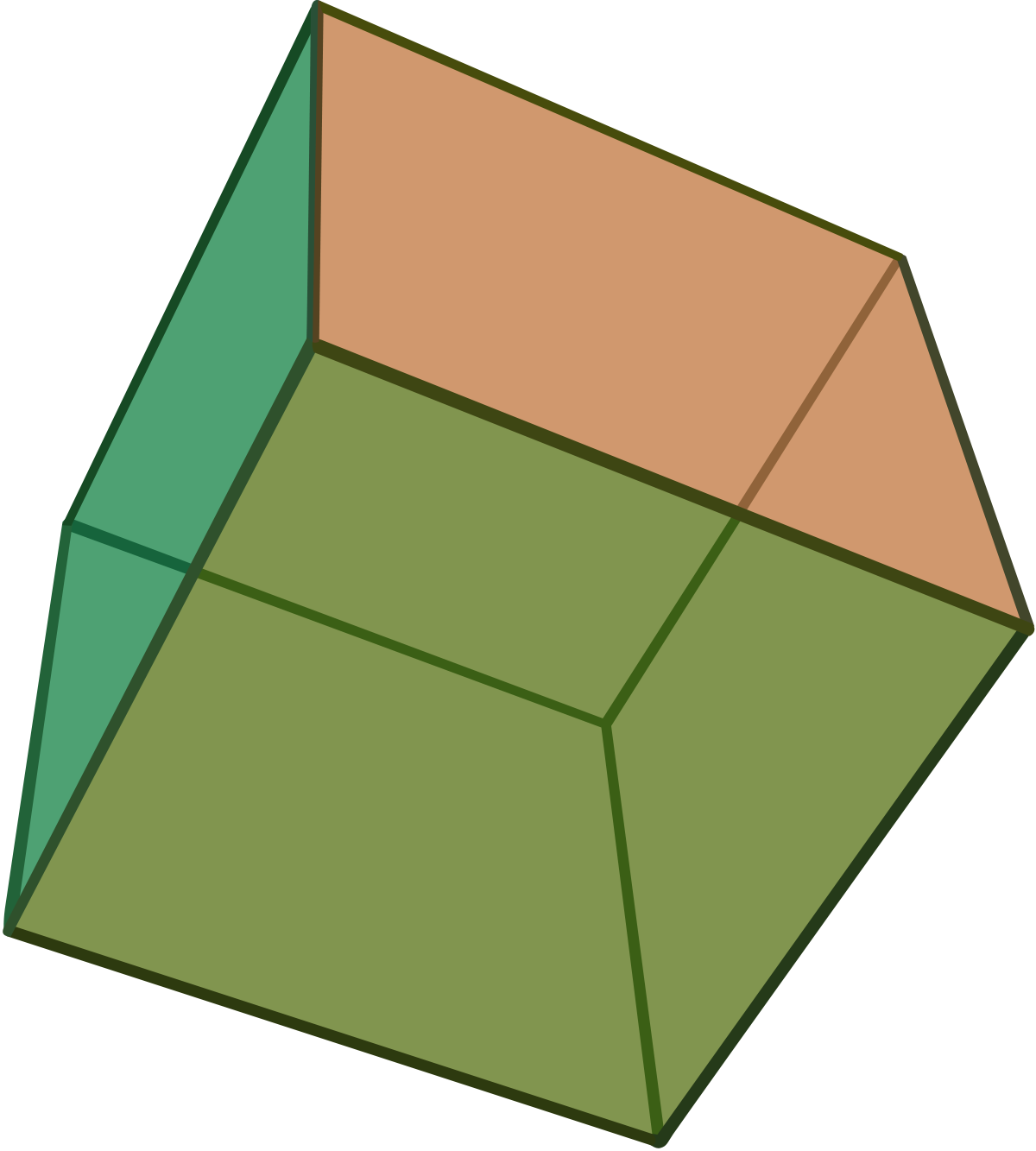
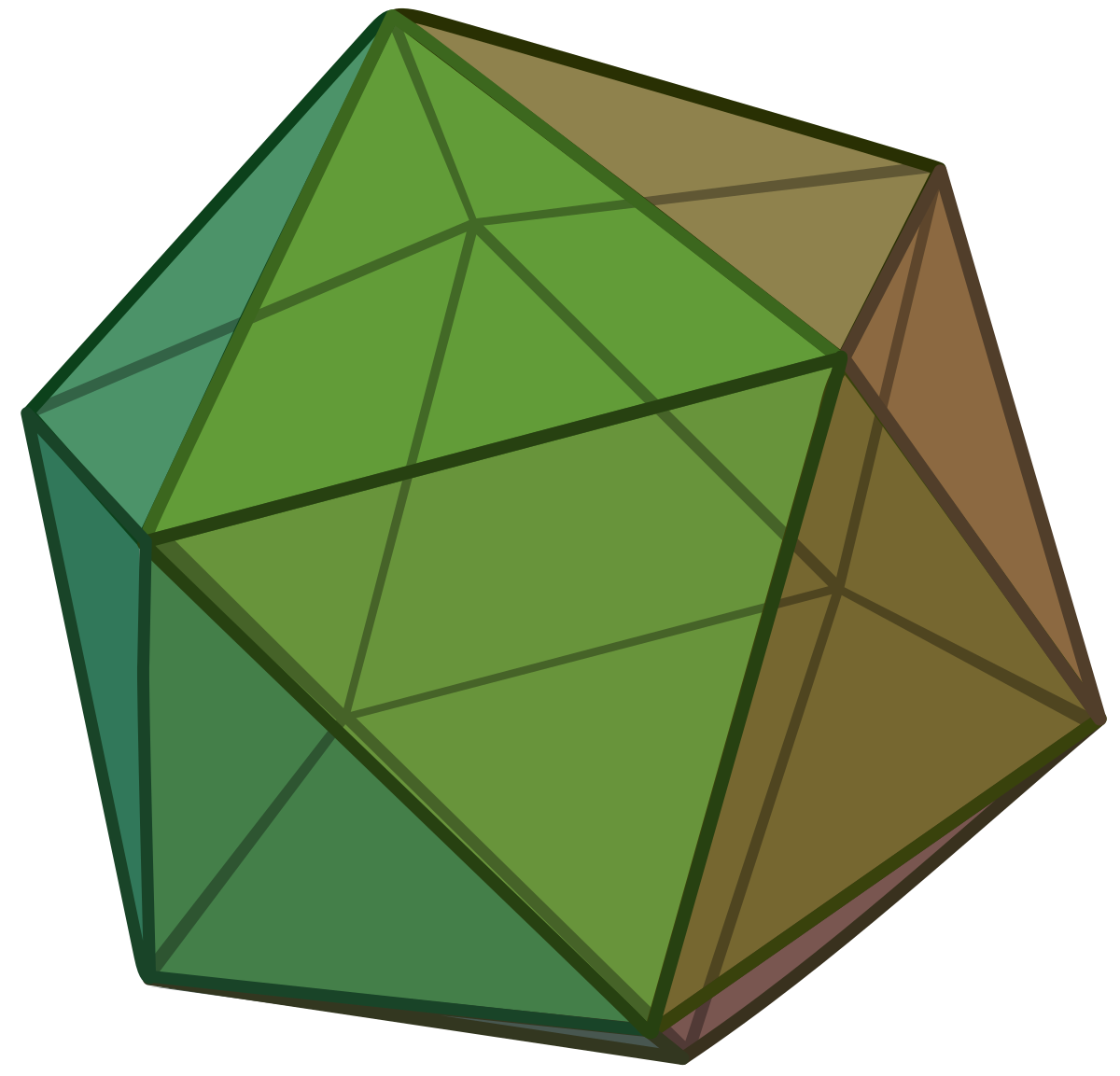
Les polyèdres réguliers sont des polyèdres dont les longueurs des côtés sont égales, les angles aux sommets sont égaux, les angles dièdres (angles entre deux faces) sont égaux. Il existe cinq polyèdres réguliers distincts de l'espace euclidien :
Ces solides sont uniques, à similitude de l'espace près. Leurs faces sont soit des triangles, soit des carrés, soit des pentagones. La liste de ces cinq solides est établie dans les éléments d'Euclide, qui en proposent de plus une construction.
Celle-ci consiste à plier convenablement un morceau d'une feuille, appelé patron. Pour l'obtenir, on découpe le polyèdre suivant certaines arêtes, en nombre suffisant pour pouvoir étaler la figure sur le plan. Remarquons que le patron est constructible à la règle et au compas.
Certains jeux pour enfants d'une dizaine d'années offre la possibilité d'expérimenter le positionnement de polygones réguliers dans l'espace, et d'expérimenter ainsi les solides platoniciens, ou encore solides d'Archimède. Par exemple, klikko est un ensemble de pièces de couleurs et de formes différentes, dont triangles, carrés et pentagones, pouvant d'accrocher par un clic (d'où le nom).
En dimension supérieure
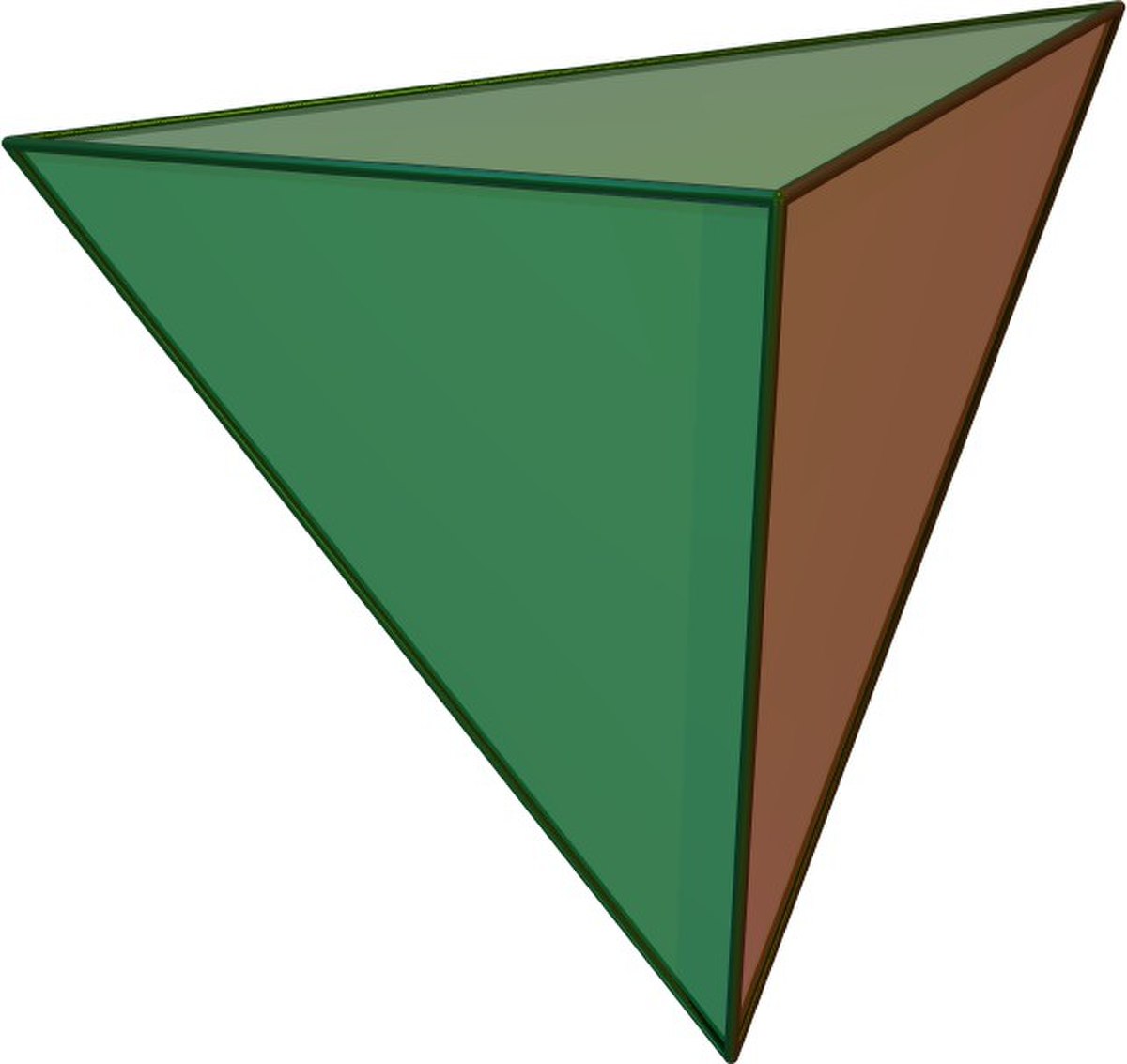
En dimension supérieure, il devient difficile de donner une description des polyèdres réguliers. Toutefois, le tétraèdre, l'octaèdre, et le cube se généralisent en toute dimension, donnant naissance à trois grandes familles de polytopes réguliers :
- Le n-simplexe régulier.
- L'hypercube.
- Le dual de l'hypercube : l'hyperoctaèdre.
Il existe également, au même titre que les solides de Platon, des polytopes réguliers quadri-dimensionnels.
Liste des polytopes réguliers
| Dimension | Nombre de polytopes convexes réguliers | Nombre de polytopes étoilés réguliers |
|---|---|---|
| 1 | 1 | 0 |
| 2 | infinité de polygones réguliers | infinité de polygones étoilés |
| 3 | 5 solides de Platon | 4 solides de Kepler-Poinsot |
| 4 | 6 polychores réguliers convexes | 10 polychores de Schläfli-Hess |
| ≥ 5 | 3 n-polytopes réguliers convexes | 0 n-polytope régulier étoilé |