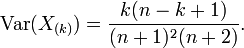Loi uniforme continue - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
| Uniforme | |
|---|---|
| |
| |
| | |
| Paramètres |
|
| Support |
|
| Densité de probabilité (fonction de masse) |  |
| Fonction de répartition |
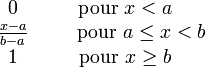
|
| Espérance |
|
| Médiane (centre) |
|
| Mode | toute valeur dans
|
| Variance |
|
| Asymétrie (statistique) |
|
| Kurtosis (non-normalisé) |
|
| Entropie |
|
| Fonction génératrice des moments |
|
| Fonction caractéristique |
|
| modifier | |
Dans la Théorie des probabilités et en statistiques, la loi uniforme continue est une famille de lois de probabilité telle que tous les intervalles de même longueur du support ont même probabilité.
La loi uniforme continue est une généralisation de la fonction rectangle à cause de la forme de sa fonction densité de probabilité. Elle est paramétrée par les plus petites et plus grandes valeurs a et b que la variable aléatoire uniforme peut prendre. Cette loi continue est souvent notée U(a,b).
Caractérisation
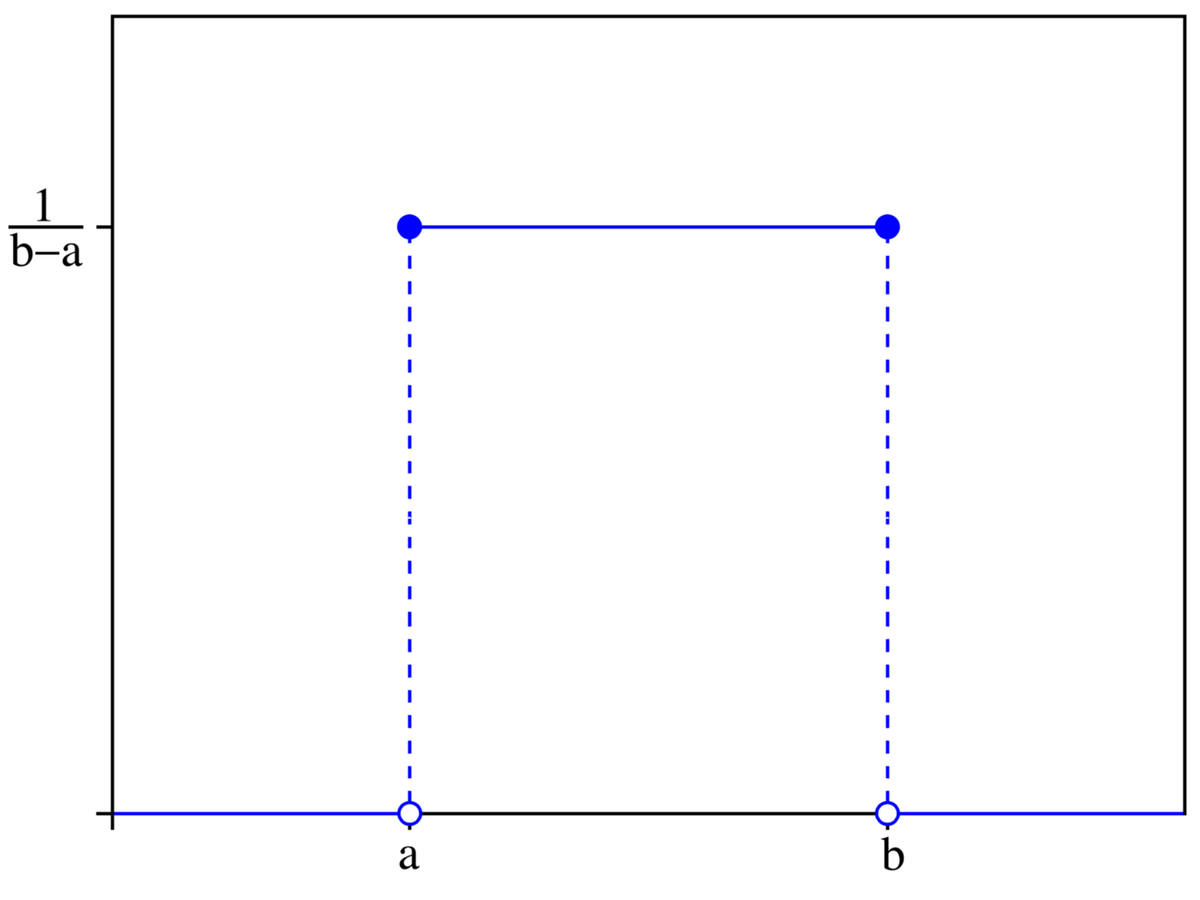
Densité
La densité de probabilité est:
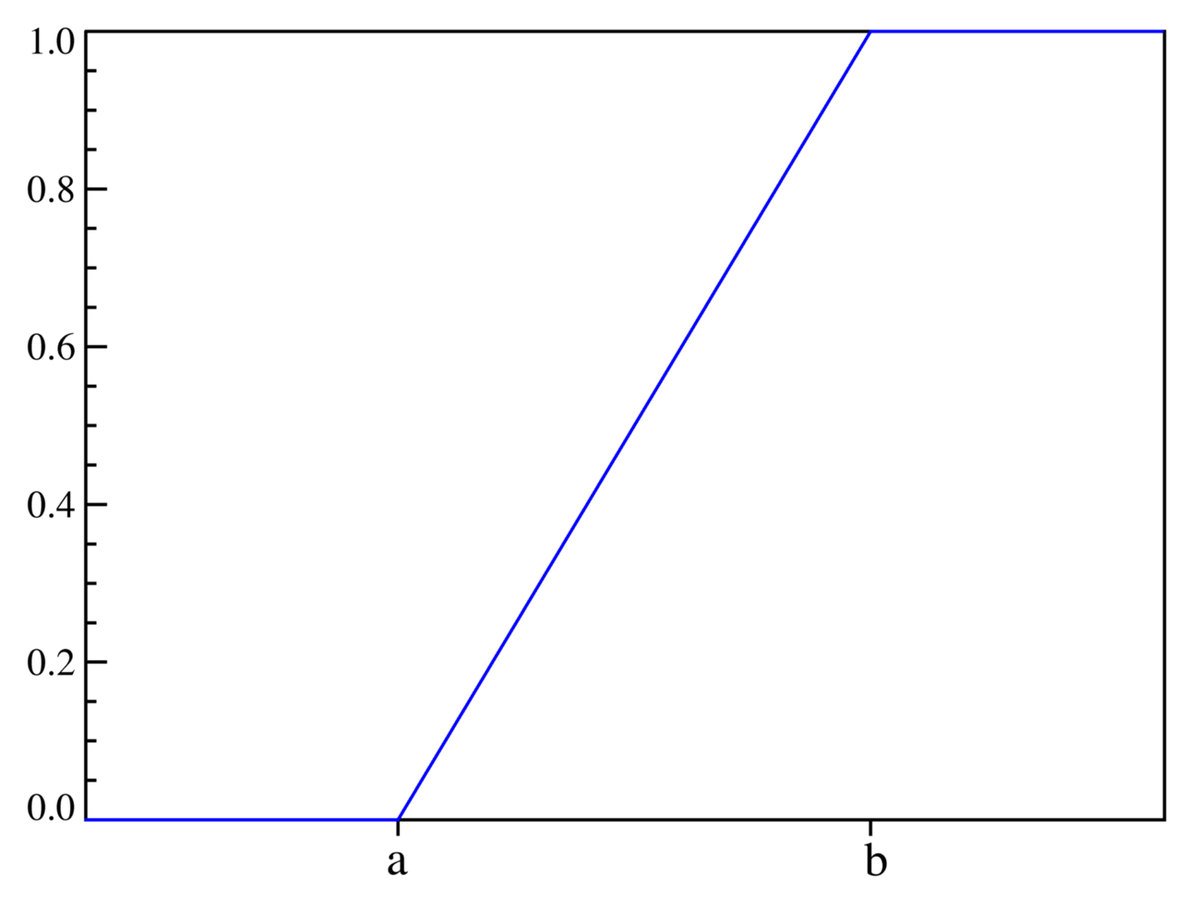
Fonction de répartition
La Fonction de répartition est donnée par
Fonctions génératrices
Fonction génératrice des moments
La Fonction génératrice des moments est
qui permet de calculer tous les moments non centrés, m k:
Ainsi, pour une Variable aléatoire suivant cette loi, l'espérance est alors m1 = (a + b)/2 et la variance est m2 − m12 = (b − a)2/12.
Fonction génératrice des cumulants
Pour n ≥ 2, le n-ième cumulant de la loi uniforme sur l'intervalle [0, 1] est bn/n, où bn est le n-ième Nombre de Bernoulli.
Loi uniforme standard
Le cas particulier a = 0 et b = 1 donne naissance à la loi uniforme standard, aussi notée U(0,1). Il faut noter le fait suivant: si u1 est distribué selon une loi uniforme standard, alors c'est aussi le cas pour u2 = 1-u1.
Propriétés
Généralisation à des tribus boréliennes
La loi uniforme se généralise à des ensembles plus complexes que les intervalles. Si S est un borélien de mesure finie non nulle, la loi uniforme sur S est spécifiée en définissant une densité nulle sur l'extérieur de S et égale à la constante 1/K sur S, où K est la mesure de Lebesgue de S.
Statistiques d'ordre
Soit X1, ..., Xn un échantillon i.i.d. issu de la loi U(0,1). Soit X(k) la k-ième Statistique d'ordre de l'échantillon. Alors, la distribution de X(k) est une Loi bêta de paramétres k et n − k + 1. L'espérance est
Ce fait est utile lorsqu'on construit une Droite de Henry.
Les variances sont
L'aspect uniforme
La probabilité qu'une variable uniforme tombe dans un intervalle donné est indépendante de la position de cet intervalle, mais dépend seulement de sa longueur, à condition que cet intervalle soit inclus dans le support de la loi. Ainsi, si X ≈ U(0,b) et que [x, x+d] est un sous-intervalle de [0,b], avec d > 0 fixé, alors
![P\left(X\in\left [ x,x+d \right ]\right) = \int_{x}^{x+d} \frac{\mathrm{d}y}{b-a}\, = \frac{d}{b-a} \,\!](https://static.techno-science.net/illustration/Definitions/autres/7/706f126a636a3d3f242cdcfc6e8478aa_0af9865c5b51d9bea2ff58ad520e7f14.png)
qui est indépendant de x. Ce fait motive la dénomination de cette loi.
Applications
En Statistiques, lorsqu'une valeur p (p-value) est utilisée dans une procédure de test statistique pour une hypothèse nulle simple, et que la distribution du test est continue, alors la valeur p est uniformément distribuée selon la loi uniforme sur [0;1] si l'hypothèse nulle est vérifiée.
Obtenir des réalisations de la loi uniforme
La plupart des langages de programmation fournissent un générateur de pseudo-nombres aléatoires, dont la distribution est effectivement la loi uniforme standard.
Si u est U(0;1), alors v = a + (b − a)u suit la loi U(a;b).
Obtenir des réalisations d'une loi continue quelconque
D'après le théorème cité plus haut, la loi uniforme permet en théorie d'obtenir des tirages de toute loi continue à densité. Il suffit pour cela d'inverser la Fonction de répartition de cette loi, et de l'appliquer à des tirages de la loi uniforme standard. Malheureusement, dans bien des cas pratiques, on ne dispose pas d'une expression analytique pour la fonction de répartition; on peut alors utiliser une inversion numérique (coûteuse en calculs) ou des méthodes concurrentes, comme la Méthode de rejet.
Le plus important exemple d'échec de la méthode de la transformée inverse est la Loi normale. Toutefois, la Méthode de Box-Muller fournit une méthode pratique pour transformer un échantillon uniforme en un échantillon normal, et ce de manière exacte.
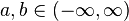
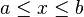
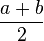
![[a,b] \,\!](https://static.techno-science.net/illustration/Definitions/autres/8/8b596d04e319e05cadcc7dcf251a9815_d0fd2a02aef5c5cb89aaff8e4ffed7c8.png)
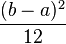
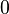

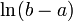
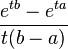
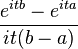
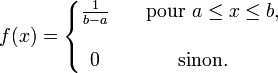
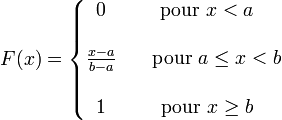
![M_x = E[e^{tx}] = \frac{e^{tb}-e^{ta}}{t(b-a)} \,\!](https://static.techno-science.net/illustration/Definitions/autres/c/cf902a56c306285ef74512b490000260_f0336edf6252bf501c28311f13dc458d.png)
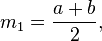
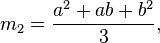
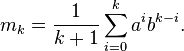
![\operatorname{E}[X_{(k)}] = {k \over n+1}.](https://static.techno-science.net/illustration/Definitions/autres/c/cbaecd0355dcd949349f0e8008a9a218_0f10a3674a65c808ec1e0dcf384d91c4.png)