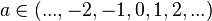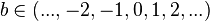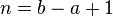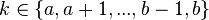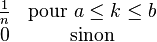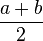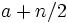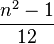Loi uniforme discrète - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
| Loi uniforme discrète | |
|---|---|
| |
| |
| | |
| Paramètres |
|
| Support |
|
| Densité de probabilité (fonction de masse) |
|
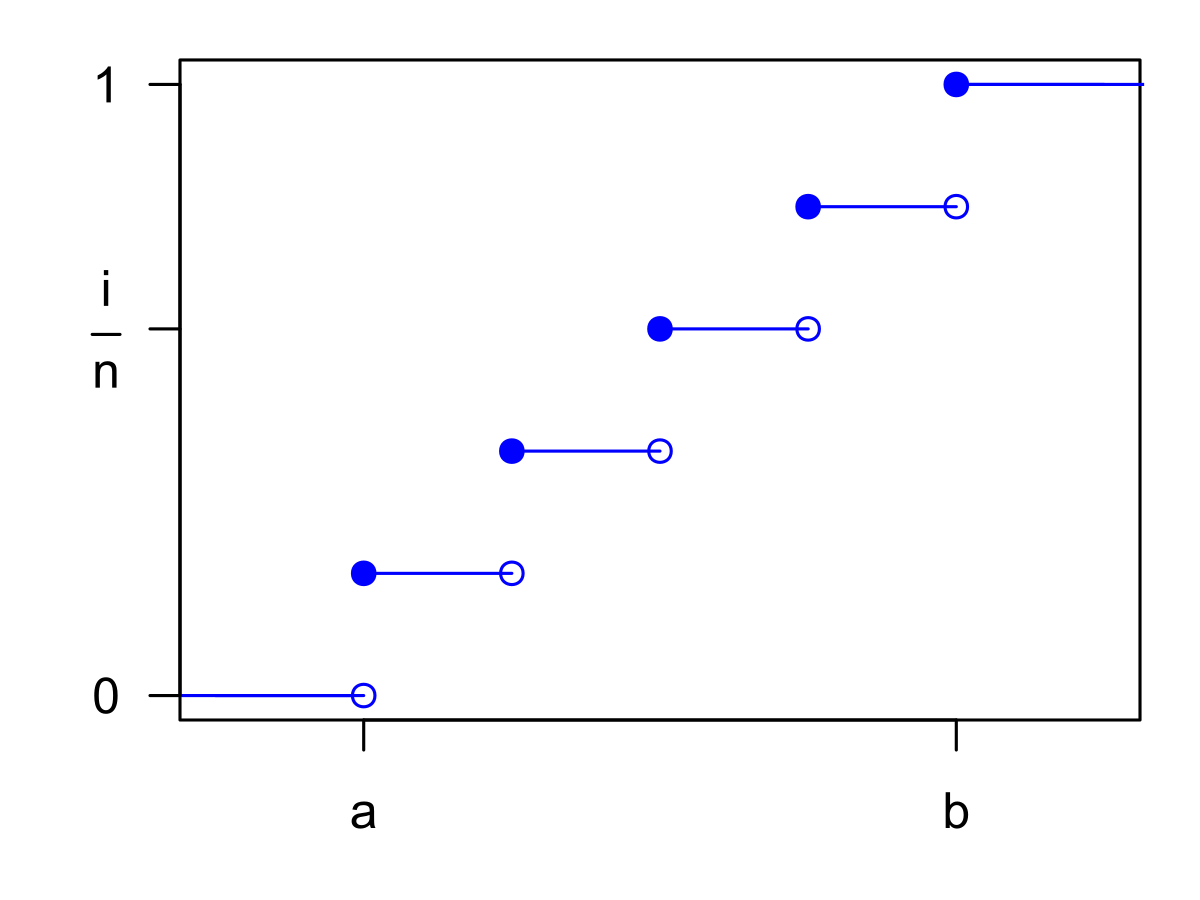
| Fonction de répartition |  |
| Espérance |
|
| Médiane (centre) |
|
| Mode | N/A |
| Variance |
|
| Asymétrie (statistique) |
|
| Kurtosis (non-normalisé) |
|
| Entropie |
|
| Fonction génératrice des moments |
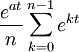
|
| Fonction caractéristique |
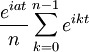
|
| modifier | |
En théorie des probabilités, la loi discrète uniforme est une loi de probabilité discrète indiquant une probabilité de se réaliser identique (équiprobabilité) à chaque valeur d’un ensemble fini de valeurs possibles.
Description
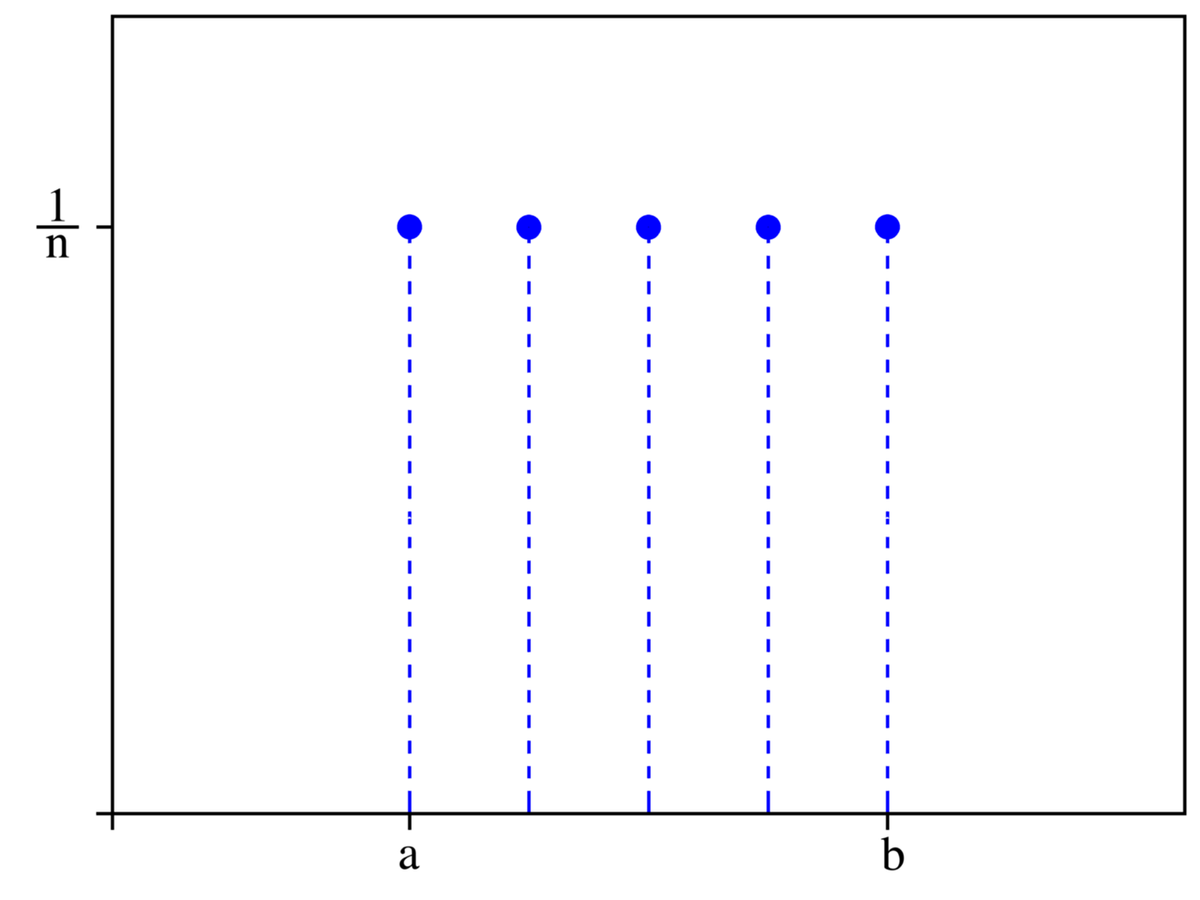
Une variable aléatoire qui peut prendre n valeurs possibles k1 ,k2 , ... , kn équiprobables, suit une loi uniforme lorsque la probabilité de n’importe quelle valeur ki est égale à 1/n .
Un exemple simple de loi discrète uniforme est le lancer d’un dé honnête. Les valeurs possibles de k sont 1, 2, 3, 4, 5, 6; et à chaque fois que le dé est lancé, la probabilité d’un score donné est égale à 1/6.
Dans le cas où les valeurs d’une variable aléatoire suivant une loi discrète uniforme sont réelles, il est possible d’exprimer la fonction de répartition en termes de distribution déterministe ; ainsi
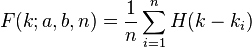
où H(x-x0 ) désigne la fonction marche de Heaviside, est la fonction de répartition (ou distribution cumulative) de la distribution déterministe centrée en x0 , aussi appelée masse de Dirac en x0 . Cela suppose que les hypothèses suffisantes soient vérifiées aux points de transition.
Cas général
Une variable aléatoire X prenant toutes les valeurs possibles d'un ensemble A (de cardinal #A=n ) avec équiprobabilité sera dite uniforme sur A.
Cas particulier important
La table ci-contre concerne la loi uniforme sur un ensemble de n entiers consécutifs, qui n'est qu'un cas particulier de loi uniforme, mais un cas particulier important : cela correspond à
![\ A\ =\ [\![a,b]\!],\qquad n=b-a+1.](https://static.techno-science.net/illustration/Definitions/autres/e/e30ba30fbac72e8d5127580b4eed71c2_6e34c9950d04634f863bf24b4d3e4bf0.png)
Calcul de probabilités et d'espérance (cas général)
Si X suit la loi uniforme sur un ensemble fini A, on dit parfois que la loi de X est
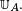
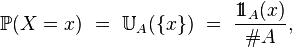
où
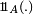
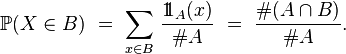
Pour une fonction φ définie sur A, à valeurs réelles, on a :
![\ \mathbb{E}\left[\phi(X)\right]\ =\ \frac{1}{\#A}\sum_{x\in A}\,\phi(x).](https://static.techno-science.net/illustration/Definitions/autres/4/45022f2b943350331c5b4c7370f43dbc_b99411a956aade1d4edafbca03a07ff3.png)
L'espérance de φ(X) est donc la valeur moyenne de φ sur A. En utilisant les notations classiques de théorie de la mesure, on traduira cela par :
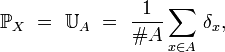
où δx désigne la masse de Dirac en x, qui a pour fonction de répartition la fonction marche de Heavyside évoquée .