Loi de probabilité à plusieurs variables - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
Dans certains problèmes interviennent simultanément plusieurs variables aléatoires. Mis à part les cas particuliers de variables indépendantes (notion définie ci-dessous) et de variables liées fonctionnellement, cela introduit la notion de loi de probabilité à plusieurs variables autrement appelée loi jointe. La description des notions correspondantes, certaines d'entre elles généralisant les notions relatives à une seule variable, est simplifiée de deux manières :
- Seules les variables continues sont considérées. Il est possible de passer aux variables discrètes en utilisant la fonction de Heaviside et la fonction de Dirac.
- Pour éviter la lourdeur des formules, l'exposé est limité à deux variables.
Formules de base
La probabilité pour que la variable aléatoire


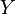
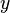
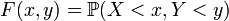
Celle-ci est non décroissante en

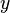
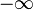
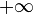
La densité de probabilité jointe ou loi jointe s'obtient par une double dérivation :
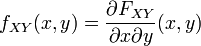
Une intégration par rapport à
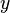


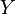
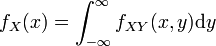
Le rapport de la densité de probabilité jointe (relative à une valeur

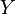


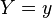
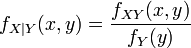
Indépendance
Si la densité de probabilité conditionnelle de

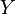
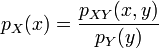
on dit que les deux variables sont indépendantes. L'égalité se réécrit :
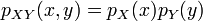
La fonction caractéristique de la somme des variables est alors égale au produit des fonctions caractéristiques individuelles :
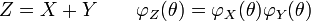
C'est l'une des principales propriétés de la fonction caractéristique. Cette remarque est, entre autres, utilisée dans la démonstration du théorème de la limite centrale.
Espérances mathématiques
L'espérance mathématique d'une fonction

![\mathbb{E}[f(X,Y)] = \int_{-\infty}^\infty \int_{-\infty}^\infty\ f(x,y) p_{XY}(x,y) \mathrm dx \mathrm dy](https://static.techno-science.net/illustration/Definitions/autres/5/582eeedf1486eec12d3ff9215d45ab59_e056e2c1a4e13771add4c113eead0df0.png)
L'opérateur espérance est linéaire ; en particulier, l'espérance (la moyenne) d'une somme de deux variables aléatoires est la somme des moyennes :
![\mathbb{E}[X + Y] = \mathbb{E}[X] + \mathbb{E}[Y]\,](https://static.techno-science.net/illustration/Definitions/autres/e/e768de1d186e115b8e33e8c4e7980d17_3ad8585f0da8176f46cb5e78d7ad38df.png)
Parmi ces espérances, une double transformation de Fourier conduit à la fonction caractéristique:
![\varphi_{XY} (\theta,\psi) = \mathbb{E}[e^{i(\theta X + \psi Y)}]](https://static.techno-science.net/illustration/Definitions/autres/2/2435062f40fef8a190ebd6659d33c3a2_26efe3eacc523afd13a1693dbd1b69e6.png)
Comme pour le cas d'une seule variable aléatoire un développement en série permet de faire apparaître les moments que l'on peut centrer par soustraction des moyennes.
Corrélation
On appelle corrélation de deux variables aléatoires la grandeur:
![\rho=\frac{\mathbb{E}[(X-\overline X) (Y -\overline Y)]}{\sigma(X)\sigma(Y)}](https://static.techno-science.net/illustration/Definitions/autres/9/95ad6c9b23a0f14fd107f3dc33c2f800_227b7418f6b97c3c4f7c4b1ade309244.png)
où
![\sigma(X)=\sqrt{\mathbb{E}[(X-\overline{X})^2]}](https://static.techno-science.net/illustration/Definitions/autres/9/9a849b54721518e49d3213cb2ef6afd8_6144f7bd9813871809875e64d00936ef.png)
![\mathbb{E}[XY] = \mathbb{E}[X] \mathbb{E}[Y]\,](https://static.techno-science.net/illustration/Definitions/autres/e/e732bcbe5c36a0f6479676a72d11c557_8f1ee6a520c31267adabcd74db5aa7e9.png)
Si les deux variables sont indépendantes, elles sont décorrélées, l'inverse n'étant pas vrai, car l'indépendance implique tous les moments au lieu d'un seul. La notion de variables décorrélées est plus faible que celle d'indépendance et est loin d'avoir la même utilité.

















































