Mathématiques du Sudoku - Définition

Introduction

Grille de Sudoku classique

Variante du Sudoku basée sur des comparaisons entre les cases

Sudoku classique avec une contrainte supplémentaire sur les diagonales

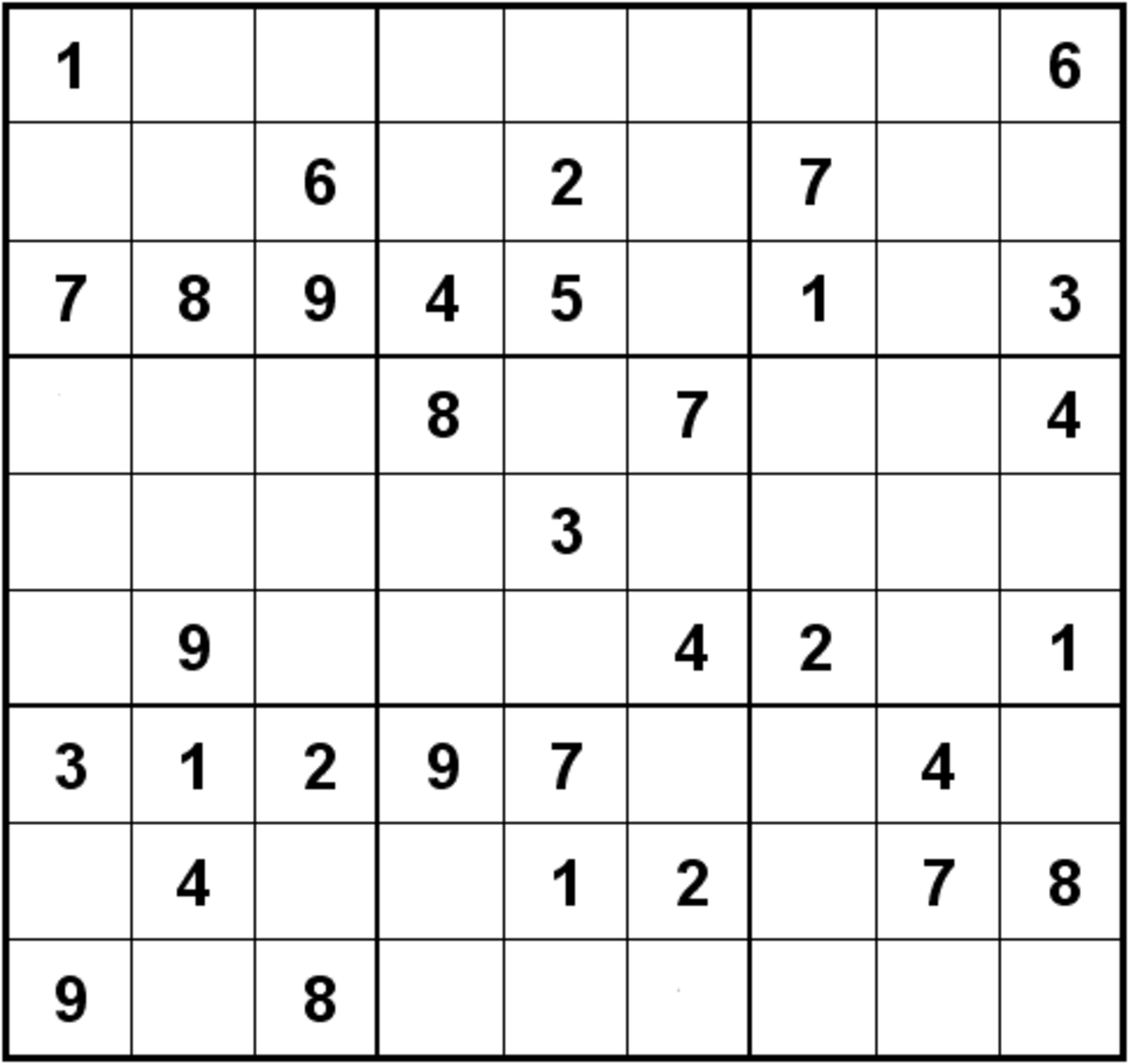
Le jeu du Sudoku consiste à compléter une grille carrée divisée en N régions de N cases, en partie remplie avec des nombres, de façon à ce que dans chaque ligne, chaque colonne et chaque région les nombres de 1 à N apparaissent une et une seule fois.

Une analyse mathématique du Sudoku permet de découvrir les différentes propriétés et problèmes qui se cachent derrière ce jeu et ses variantes.

Introduction

L'analyse mathématique du Sudoku se divise en deux grandes parties : l'analyse des propriétés des grilles complètes et l'analyse de la résolution d'une grille.

L'analyse des grilles s'est en grande partie focalisée sur l'énumération des solutions possibles pour différentes variantes du jeu. L'étude de la résolution se concentre sur les valeurs initiales de la grille et sur les étapes qui mènent à la grille complète. Ces techniques font appel à plusieurs disciplines : analyse combinatoire, algorithmique, théorie des groupes ainsi que la programmation puisque l'ordinateur permet de rapidement résoudre les grilles.

Il y a un grand nombre de variantes du Sudoku, en général caractérisées par la taille de la grille (le paramètre N) et la forme des régions. Les Sudoku classiques ont un N égal à 9 avec des régions de 3x3 cases. Un Sudoku rectangulaire possède des régions rectangulaires d'une taille L×C où L est le nombre de lignes et C le nombre de colonnes. Un tel Sudoku, avec une taille de L×1 (ou 1×C), devient un carré latin puisque la région est une ligne ou une colonne unique.

Des variantes plus complexes existent comme celles avec des régions découpées de manière irrégulière (Nanpure), avec des contraintes supplémentaires (Samunamupure ou Killer Sudoku, respect de l'unicité sur les diagonales avec le Kokonotsu, contraintes sur l'ordre des éléments avec le Greater-Than) ou des assemblages de plusieurs grilles (Samurai, Sudoku en 3D). Dans certaines variantes, les chiffres sont remplacés par des lettres. Cette substitution des caractères utilisés ne change toutefois rien aux propriétés intrinsèques du puzzle si les règles restent les mêmes.

L'analyse mathématique du Sudoku a suivi la popularité du jeu. Les analyses concernant la complexité algorithme et le caractère NP-complet du jeu furent documentés vers la fin de l'année 2002, les résultats d'énumération ont fait leur apparition vers le milieu de l'année 2005. Les contributions des nombreux chercheurs et amateurs ont permis de mettre à jour les propriétés du jeu. L'apparition des variantes du Sudoku étend d'autant plus les éléments mathématiques à considérer et explorer.

Contrastant avec les deux approches mathématiques principales citées au début, une approche basée sur la logique mathématique et s'attaquant au problème de la résolution des puzzles a été proposée récemment dans le livre de Denis Berthier, "The Hidden Logic of Sudoku" (La logique cachée du Sudoku). Cela a permis de découvrir et de formaliser toutes les symétries généralisées du jeu et de découvrir de nouvelles règles de résolution basées dessus, comme les chaînes xy cachées.

Nombre de grilles complètes possibles

Le nombre de grilles complètes possibles est inférieur à 9!⁹ qui correspond au nombre de façons de construire les régions sans tenir compte des contraintes sur les lignes et les colonnes.

En 2005, Bertram Felgenhauer et Frazer Jarvis ont prouvé que ce nombre de grilles était de :

6 670 903 752 021 072 936 960≈6,67.10²¹ (pour plus de détails, voir (en) [4] et suite A107739 de l’OEIS).

Ce nombre est égal à :

9!×72²×2⁷×27 704 267 971

Le dernier facteur est un nombre premier. Ce résultat a été prouvé grâce à une recherche exhaustive. Frazer Jarvis a ensuite considérablement simplifié la preuve grâce à une analyse détaillée. La démonstration a été validée de manière indépendante par Ed Russell. Jarvis et Russell ont par la suite montré qu'en tenant compte des symétries, il y avait 5 472 730 538 solutions [5] (pour plus de détails, voir (en) [6] et suite A109741 de l’OEIS).

En revanche, à cette date, aucun résultat n'existe sur le nombre de grilles complètes dans un super sudoku (grille 16 × 16). Si maintenant, on s'intéresse aux nombres de problèmes proposables, ce nombre est nettement plus important car il existe plusieurs façons de révéler les chiffres d'une même grille.

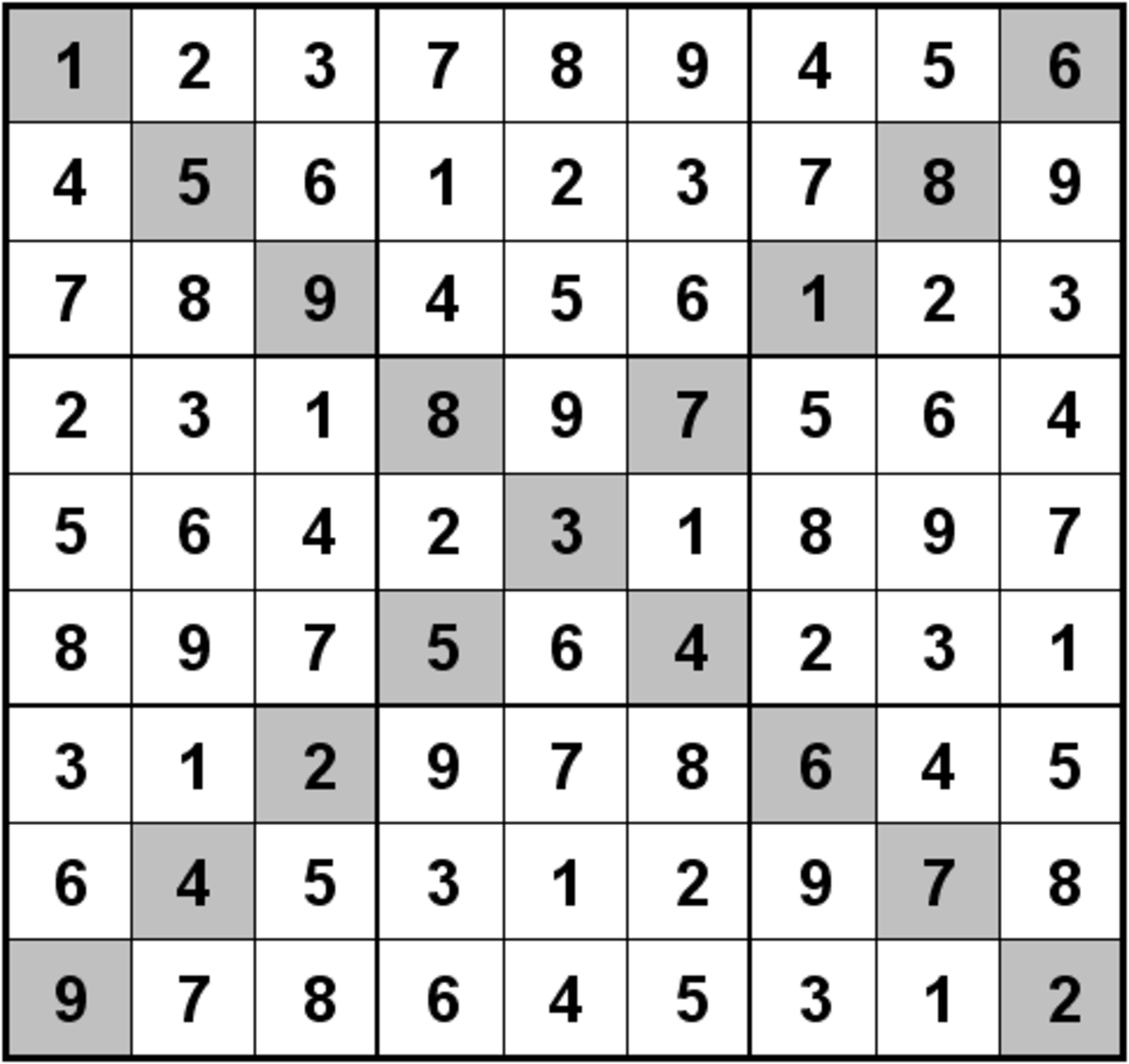
Le problème de savoir combien de cases remplies sont nécessaires au préalable pour rendre la résolution unique est, à ce jour, sans réponse. Le meilleur résultat, obtenu par des Japonais, est de 17 cases sans contrainte de symétrie. [7] [8]. Rien ne dit que ce ne soit pas possible avec moins de nombres. Gordon Royle indique que deux résolutions sont considérées comme différentes si elles ne peuvent pas être transformées l'une vers l'autre (ou l'inverse) grâce à une combinaison des opérations suivantes :

1. permutations des 9 nombres
2. échange des lignes avec les colonnes (transposition)
3. permutation des lignes dans un seul bloc
4. permutation des colonnes dans un seul bloc
5. permutation des blocs sur une ligne de blocs
6. permutation des blocs sur une colonne de blocs

On remarque l'analogie avec les opérations matricielles en algèbre linéaire.

Terminologie

Un puzzle est une grille incomplète où figurent des valeurs initiales. Les régions sont également appelées des blocs ou des zones. Le terme de carré est évité pour lever toute confusion.

Une bande est une suite de blocs adjacents sur l'axe horizontal. Une pile est une suite de blocs adjacents sur l'axe vertical. Dans un Sudoku de 9x9 cases, il y a ainsi 3 bandes et 3 piles.

Un Sudoku correctement conçu a une et une seulement solution : la grille finale est unique, mais la résolution à partir de la grille partielle peut toutefois prendre des chemins différents.

Formalisation des différentes variantes

Une région peut être décrite par ses dimensions : LxC où L est le nombre de lignes et C le nombre de colonnes dans la région. Dans la version classique du Sudoku, L = C = 3. Cela implique qu'il existe L régions par bande et C régions par pile. Il est plus pratique de mentionner la taille de la région plutôt que le nombre d'éléments car une région de 2x6 a le même nombre de cases que celle de 3x4.

La découpe suivante peut être adoptée pour classifier grossièrement les variantes :

• régions rectangulaires
  • régions carrées
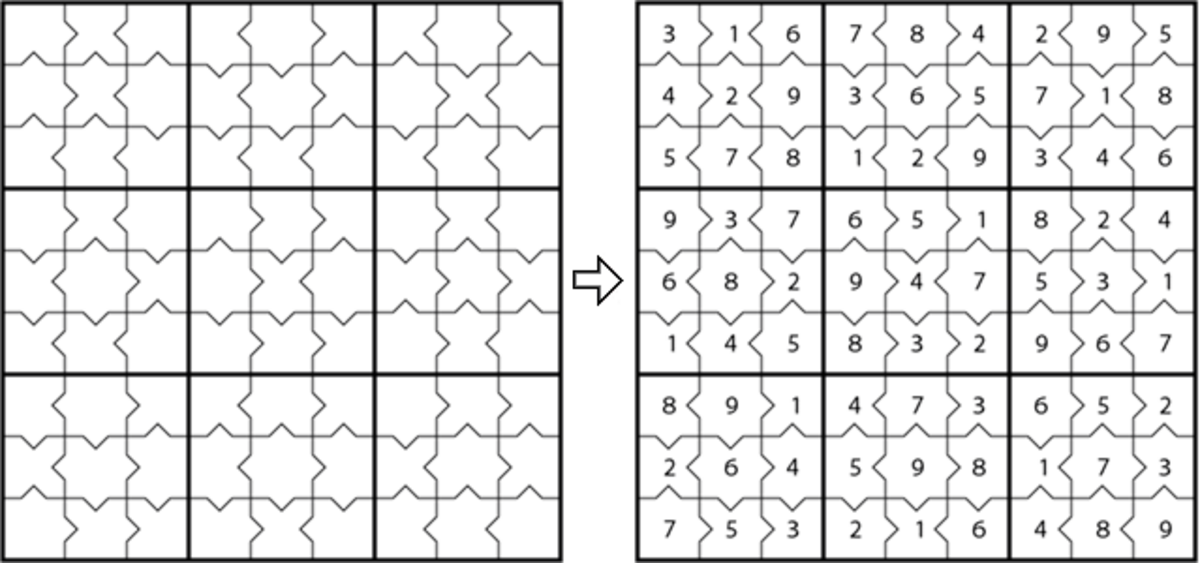
• régions irrégulières (polyomino)

Des contraintes supplémentaires permettent de mieux cibler le type de jeu.

Un Sudoku carré de NxN régions possède plusieurs propriétés respectées pour tous ses sous-éléments, en plus de la règle classique de l'absence de doublons. En effet, chaque ligne et chaque colonne a une intersection avec N régions et partage N cases avec chacune d'entre elles. Le nombre de bandes et de piles est aussi égal à N. Le Sudoku rectangulaire n'a pas ces propriétés.

Le Sudoku avec des régions de 3x3 cache une autre propriété qui lui est propre : N est le nombre de sous-unités considérées dans le jeu, à savoir trois : la ligne, la colonne et la région.

Définitions

Soit :

• s une solution d'un Sudoku avec des dimensions spécifiques et qui satisfait les règles du Sudoku original (pas de doublons dans les lignes, colonnes et régions)
• S = {s}, l'ensemble de toutes les solutions possibles
• |S|, la cardinalité (taille) de l'ensemble S (ie. le nombre de solutions)

Le nombre de solutions dépend de la taille de la grille, des règles appliquées et de la définition précise d'une solution distincte. Pour un Sudoku avec des régions de 3x3, les conventions pour l'affichage du contenu de la grille sont les suivantes : les bandes sont labelisées du haut vers le bas, les piles de la gauche vers la droite. Les régions sont donc numérotés de la gauche vers la droite et du haut vers le bas. Cette convention s'applique aussi pour les grilles rectangulaires.

D'autres termes sont utiles dans le cas du Sudoku avec des régions de 3x3 :

• le triplet est une combinaison non-ordonnée de trois valeurs présentes sur une ligne ou une colonne d'une région. Par exemple, le triplet {3, 5, 7} signifie que les valeurs 3, 5, 7 apparaissent dans une ligne ou une colonne de la région, mais sans spécifier leur ordre d'apparition (on pourrait avoir une ligne avec 5, 7, 3 ou encore une colonne avec 3, 7, 5). Les valeurs d'un triplet peuvent être arrangées de 6 manières différentes (3!) grâce à des permutations. Par convention, les éléments d'un triplet sont écrits dans l'ordre croissant mais cela ne signifie pas qu'ils apparaissent dans la grille selon le même ordre ;
  • la notation hRL indique un triplet pour la région R et la ligne Lde la grille. Le préfixe h indique qu'il s'agit d'un triplet horizontal ;
  • de manière similaire, la notation vRC identifie un triplet pour la région R et la colonne C de la grille. Le préfixe v indique qu'il s'agit d'un triplet vertical.

Par exemple, la notation h56 correspond au triplet de la région 5, ligne 6. En anglais, on utilise la notation r pour row et c pour column.

On parle aussi de mini-ligne ou de mini-colonne pour désigner la portion présente dans une région d'une ligne ou d'une colonne de la grille.