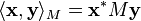Matrice définie positive - Définition

Propriétés

Les propriétés suivantes sont communes aux matrices symétriques réelles et aux matrices complexes hermitiennes.

1. Toute matrice définie positive est inversible (à déterminant réel strictement positif), et son inverse est elle aussi définie positive.
2. Si M est définie positive et r est un nombre réel strictement positif, alors rM est définie positive.
3. Si M et N sont définies positives, alors M + N est définie positive.
4. Si M et N sont définies positives, et si MN = NM (on dit qu'elles commutent), alors MN est définie positive.
5. Une matrice M est définie positive si et seulement s'il existe une matrice définie positive A telle que A² = M ; dans ce cas, la matrice définie positive A est unique, et on peut la noter A = M^{1 / 2} (voir l'article racine carrée d'une matrice).

Cette propriété est utilisée pour la décomposition polaire.

Matrice hermitienne définie positive

On étend les propriétés et définitions précédentes aux matrices complexes hermitiennes.

Soit M une matrice hermitienne d'ordre n. Elle est dite définie positive si elle vérifie l'une des 3 propriétés équivalentes suivantes :

1.	Pour toute matrice colonne non nulle à n éléments complexes, on a .
2.	Toutes les valeurs propres de M sont strictement positives, c'est-à-dire : .
3.	La forme hermitienne définie par la relation est un produit scalaire sur (identifié ici à l'espace vectoriel des matrices colonnes à n éléments complexes).

Une matrice hermitienne est dite définie négative si son opposée (hermitienne elle aussi) est définie positive.

Critère de Sylvester

Pour qu'une matrice , réelle symétrique ou complexe hermitienne, soit définie positive, il faut et suffit que les n matrices aient leur déterminant strictement positif, autrement dit que tous les mineurs principaux aient leur déterminant strictement positif.

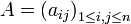
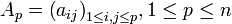
Remarque 1. Pour n=2, le critère de Sylvester est essentiellement le critère de positivité du trinôme du second degré.

Remarque 2. Plus généralement, l'indice d'une matrice symétrique réelle est égal au nombre de changements de signes dans la suite de ses n + 1 mineurs principaux (en incluant det(A₀) = 1), sous réserve que tous soient non nuls.

Remarque 3. En fait sur un corps (commutatif) quelconque, cette condition de non-nullité des mineurs principaux est une condition nécessaire et suffisante pour qu'il existe une matrice Q triangulaire supérieure telle que ^tQAQ soit diagonale et de rang maximum (il suffit d'adapter la démonstration qui suit).

Preuve. Notons q la forme quadratique associée à A, définie par .

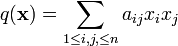
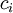
La condition est nécessaire. On remarque d'abord que si q est définie positive, alors . En effet, par rapport à une base orthogonale pour cette forme quadratique (il en existe, d'après la réduction de Gauss), la matrice de q s'écrit les étant tous strictement positifs. Alors (Q étant la matrice de passage), donc . Le résultat s'ensuit, en appliquant le même raisonnement à la restriction de q aux sous-espaces , pour .

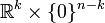
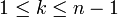
Montrons maintenant que la condition est suffisante. On procède par récurrence sur la dimension. Pour n=0 c'est évident puisqu'en dimension 0 l'ensemble des vecteurs non nuls est vide. Supposons la propriété vraie pour n-1 et notons . Par hypothèse de récurrence, est définie positive. De plus, q est est non dégénérée (parce que ) donc

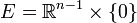
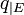
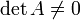
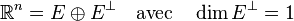
Soient e un vecteur non nul de et a = q(e). Alors et ont même signe d'après le même argument que dans la première partie (qui met implicitement en jeu le discriminant), or par hypothèse et sont strictement positifs. Donc a>0, si bien que la restriction de q à est, elle aussi, définie positive, ce qui montre que q est définie positive.

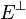
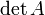
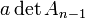
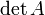
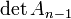
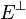
Dans le cas complexe, la preuve est analogue, en considérant la forme hermitienne définie par la matrice.