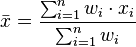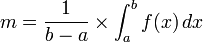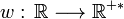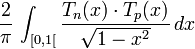Moyenne - Définition

Extensions de la notion de moyenne

Au delà des définitions précédentes de moyenne, il existe d'autres approches plus étendues pour cette notion :

Moyenne glissante

La moyenne glissante est une notion statistique, où la moyenne au lieu d'être calculée sur n valeurs fixes, est calculée sur n valeurs consécutives « glissantes ».

Ce type de calcul est aussi utilisé en informatique pour minimiser la taille mémoire nécessaire au stockage des valeurs intermédiaires. Différentes formules de moyennes glissantes existent, par exemple pour une moyenne glissante de période n :

(une moyenne glissante de période 0 ne prend qu'un terme)

(formule de récurrence)

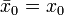
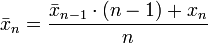
Moyenne réduite

C'est une fonction disponible dans le logiciel Excel qui sert à exclure des valeurs hors norme qui faussent la moyenne. La syntaxe est la suivante : MOYENNE.REDUITE(matrice;pourcentage) La donnée "matrice" est tout simplement la plage de donnée sur laquelle porte le calcul de moyenne. Le pourcentage est une donnée qui donne à la fonction l'information sur le nombre de valeurs à exclure.Ce nombre est arrondi au nombre pair le plus proche car la fonction enlève systématiquement un nombre de plus grandes valeurs et un même nombre de plus petite valeurs, ce qui en tout fait un nombre pair de valeurs à exclure.

Moyenne pondérée

La moyenne pondérée est utilisée, en géométrie pour localiser le barycentre d'un polygone, en physique pour déterminer le centre de gravité ou en statistique et probabilité pour calculer une espérance. On la calcule ainsi :

Dans le cas général le poids w_i représente l'influence de l'élément x_i par rapport aux autres.

A noter qu'il s'agit ici de la moyenne pondérée arithmétique. Il existe aussi des versions pondérées des autres moyennes, comme la moyenne géométrique pondérée et la moyenne harmonique pondérée.

Valeur moyenne d'une fonction

Pour toute fonction continue (ou même seulement continue par morceaux) sur un segment [a, b] non vide et non trivial (ie b > a), la valeur moyenne de ƒ sur [a, b] est le réel m défini par :

Cette notion généralise celle de moyenne d'un nombre fini de réels en l'appliquant à un nombre infini de valeurs prises par une fonction intégrable. Elle sert par exemple dans la décomposition en série de Fourier d'une fonction périodique : c'est la composante constante. En traitement du signal, pour les signaux périodiques, il s'agit de la composante continue (offset).

On peut aussi, par analogie avec les moyennes pondérées d'un nombre fini de réels, affecter « à chacune des valeurs prises par la fonction » un coefficient strictement positif. On utilise alors ce que l'on appelle une fonction poids

(w pour l'initiale de weight, poids en anglais) :

.

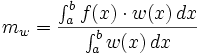
Ce procédé peut aussi s'utiliser sur un intervalle ouvert ou semi-ouvert mais borné (ie aucune de ses bornes n'est infinie) où la fonction ƒ×w est intégrable. On peut citer l'exemple classique servant à montrer l'orthogonalité de la famille des polynômes de Tchebychev :

où la fonction T_n×T_p est continue sur le fermé [0,1] et où la fonction poids est

est intégrable sur [0,1[, et dont l'intégrale vaut .

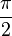
Nota : Lorsque la fonction est périodique de période T, elle a la même valeur moyenne sur toute période [a, a + T]. Cette valeur commune est appelée valeur moyenne de la fonction. Ainsi la fonction cosinus est de moyenne nulle, son carré de moyenne 1/2.