Moyenne - Définition
La liste des auteurs de cet article est disponible ici.
Les différentes moyennes
Selon la manière dont le 'total' des individus est calculé (voir ci-dessus en Statistique), il existe différentes moyennes :
Moyenne arithmétique
La moyenne arithmétique est la moyenne « ordinaire », c'est-à-dire la somme des valeurs numériques (de la liste) divisée par le nombre de ces valeurs numériques. Exemple : la hauteur moyenne des toits d'une rue.
La moyenne arithmétique se note A(x) quand des moyennes différentes sont présentes.
Exemple: Si un rectangle a pour côtés 3 et 7, alors le carré (c'est-à-dire le rectangle moyen) qui a le même périmètre P a pour côté la moyenne arithmétique de 3 et 7, c'est-à-dire 5.
Si les valeurs sont affectées de coefficients, on peut définir la moyenne arithmétique pondérée :
Étant donné un ensemble de données
ainsi que les poids non-négatifs correspondants
la moyenne arithmétique pondérée
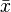
-
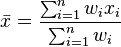
Moyenne géométrique
La moyenne géométrique est définie de la manière suivante :
On peut illustrer la moyenne géométrique avec les deux cas suivants :
- Si l'inflation d'un pays est de 5% la première année et de 15% la suivante, l'augmentation moyenne des prix se calcule grâce à la moyenne géométrique des coefficients multiplicateurs 1,05 et 1,15 soit une augmentation moyenne de 9,88% et non grâce à la moyenne arithmétique 10% (réponse intuitive).
- Le carré (c'est-à-dire le rectangle moyen à deux côtés égaux) qui a même surface (le total considéré ici) qu'un rectangle de côtés 3 et 7 a pour côté la moyenne géométrique des deux côtés du rectangle
![\sqrt[2]{3*7}](https://static.techno-science.net/illustration/Definitions/autres/0/0a3f1e7deb7988952f690fa8d0815c2a_64eaf9a88de4818baf2233a45cc5fe21.png)
La moyenne géométrique se note G(x) quand des moyennes différentes sont présentes.
Il existe une moyenne géométrique pondérée, définie ci-dessous.
Étant donné en ensemble de données
-
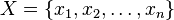
ainsi que les poids correspondants
-
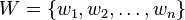
la moyenne géométrique pondérée est calculée comme étant:
Moyenne harmonique
La moyenne harmonique est définie de la manière suivante :
Si un train fait un trajet aller-retour entre 2 villes à la vitesse constante v1 pour l'aller et à la vitesse constante v2 au retour, la vitesse moyenne du trajet total n'est pas la moyenne arithmétique des 2 vitesses, mais leur moyenne harmonique.
Exemple: Si un rectangle a pour côtés 3 et 7, alors le carré (c'est-à-dire le rectangle moyen) qui a le même rapport
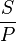
La moyenne harmonique se note H(x) quand des moyennes différentes sont présentes.
Il existe une moyenne harmonique pondérée, définie ci-dessous.
Étant donné en ensemble de données
-
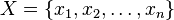
ainsi que les poids correspondants,
la moyenne harmonique pondérée est calculée comme étant:
Moyenne quadratique
La moyenne quadratique, ou RMS (pour Root Mean Square), est définie de la manière suivante :
Exemple: Si un rectangle a pour côtés 3 et 7, le carré (c'est-à-dire le rectangle moyen) qui a même diagonale (le total considéré ici) que ce rectangle, a pour côté la moyenne quadratique de 3 et 7, c'est-à-dire 5,3852.
La racine carrée de la moyenne du carré des valeurs instantanées d'une grandeur est appelée valeur quadratique moyenne, ou encore (par analogie avec l'électricité) valeur efficace.
La moyenne quadratique se note Q(x) quand des moyennes différentes sont présentes.
Comparaison entre les moyennes précédentes
Si a et b sont deux réels strictement positifs tels que a < b, alors on a :
Pour démontrer ces comparaisons et les généraliser, on fait appel à la notion de fonction convexe.
Moyenne énergétique
La moyenne énergétique est définie de la manière suivante :
C'est la moyenne de valeurs données en décibels, par exemple en acoustique.
Cas général
Si nous notons

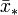

Cette équation peut être résolue s'il existe un isomorphisme (que nous noterons
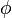

Rappelons qu'un isomorphisme est une bijection telle que l'image d'un composé est le composé des images, c'est-à-dire que, pour tout x et tout y :
Nous pouvons alors écrire :
Cette formule généralise et synthétise tous les cas précédents. Nous retrouvons par exemple :
- la moyenne énergétique si :
-
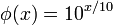
- ou la moyenne géométrique quand :
-
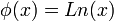
Un cas particulier important est celui où l'isomorphisme
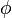
La moyenne, notée dans ce cas
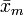
où l'on retrouve :
- pour m = 1, la moyenne arithmétique,
- pour m = 2, la moyenne quadratique,
- pour m = -1, la moyenne harmonique;
- lorsque m → 0, la limite de
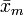
- lorsque m → +∞, la limite de
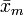
- lorsque m → -∞, la limite de
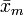
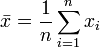
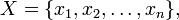
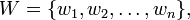
![\bar{x} = \sqrt[n]{\prod_{i=1}^n{x_i}}](https://static.techno-science.net/illustration/Definitions/autres/1/10a4a5b69d8b2cd60dd7423fb4a71b9a_f7884fc63840cabfcf5bc129881698f6.png)
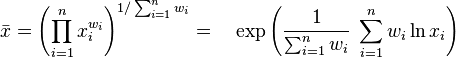
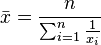
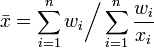
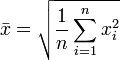
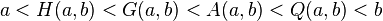
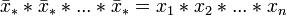
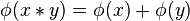
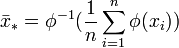
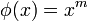
![\bar{x}_m = \sqrt[m]{\frac{1}{n}\sum_{i=1}^n{x_i^m}}](https://static.techno-science.net/illustration/Definitions/autres/e/e6efeceb54da5865dcd5b323e1c48e0a_aaca6fde5b55dfc38c5e961941ead873.png)

















































