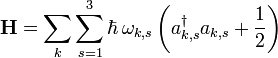Phonon - Définition
La liste des auteurs de cet article est disponible ici.
Définition des phonons
Les phonons n'existent qu'au sein d'un réseau cristallin comportant un grand nombre de particules et les seules structures physiques connues correspondant à cette définition sont les solides cristallins. Dans la suite nous ne traiterons donc des phonons que dans ce cadre et, pour la clarté de l'exposé, nous appellerons les particules constituant le réseau « atomes », bien qu'il puisse s'agir d'ions dans un solide ionique.
Aspects mécaniques : mouvement de particules dans un réseau
Dans un solide, il existe des forces d'interaction (force de van der Waals, forces covalentes, etc.) qui maintiennent chaque atome près d'une position d'équilibre. Ce sont principalement des forces de type électrique, les forces de type magnétique étant généralement négligeables. L'interaction entre chaque paire d'atomes peut être caractérisée par une fonction d'énergie potentielle V qui ne dépend que de la distance entre ces atomes et qui est la même pour toutes les paires d'atomes. L'énergie potentielle du réseau dans son ensemble est la somme des énergies potentielles d'interaction de chaque paire :
où ri est la position du ième atome, et le facteur 1/2 compense le fait que chaque paire est comptée deux fois (comme (i,j) et comme (j,i)).
Cette expression, caractéristique d'un problème à N corps, ne se prête pas à une résolution que ce soit en mécanique classique ou en mécanique quantique. Il est donc nécessaire de procéder à des approximations pour poursuivre l'analyse. Les deux approximations généralement employées sont :
- restreindre la sommation aux atomes voisins. En effet, bien que rigoureusement les forces électriques aient une portée infinie dans un solide réel, cette approximation est valide car les forces s'exerçant sur des atomes éloignés sont écrantées et donc négligeables.
- considérer que le potentiel V est un potentiel harmonique, ce qui est valide lorsque les atomes restent proches de leurs positions d'équilibre. (Formellement, cette hypothèse s'applique en effectuant un développement de Taylor du potentiel V autour de la valeur d'équilibre et en ne gardant que le premier terme non-constant, qui est d'ordre 2.)
Il est possible de relâcher l'une ou l'autre des hypothèses, pour la première en considérant l'interaction avec des voisins plus éloignés et pour la deuxième en ajoutant des termes d'ordres supérieurs. Dans la plupart des cas, l'inclusion de ces termes ne modifie pas significativement la solution.
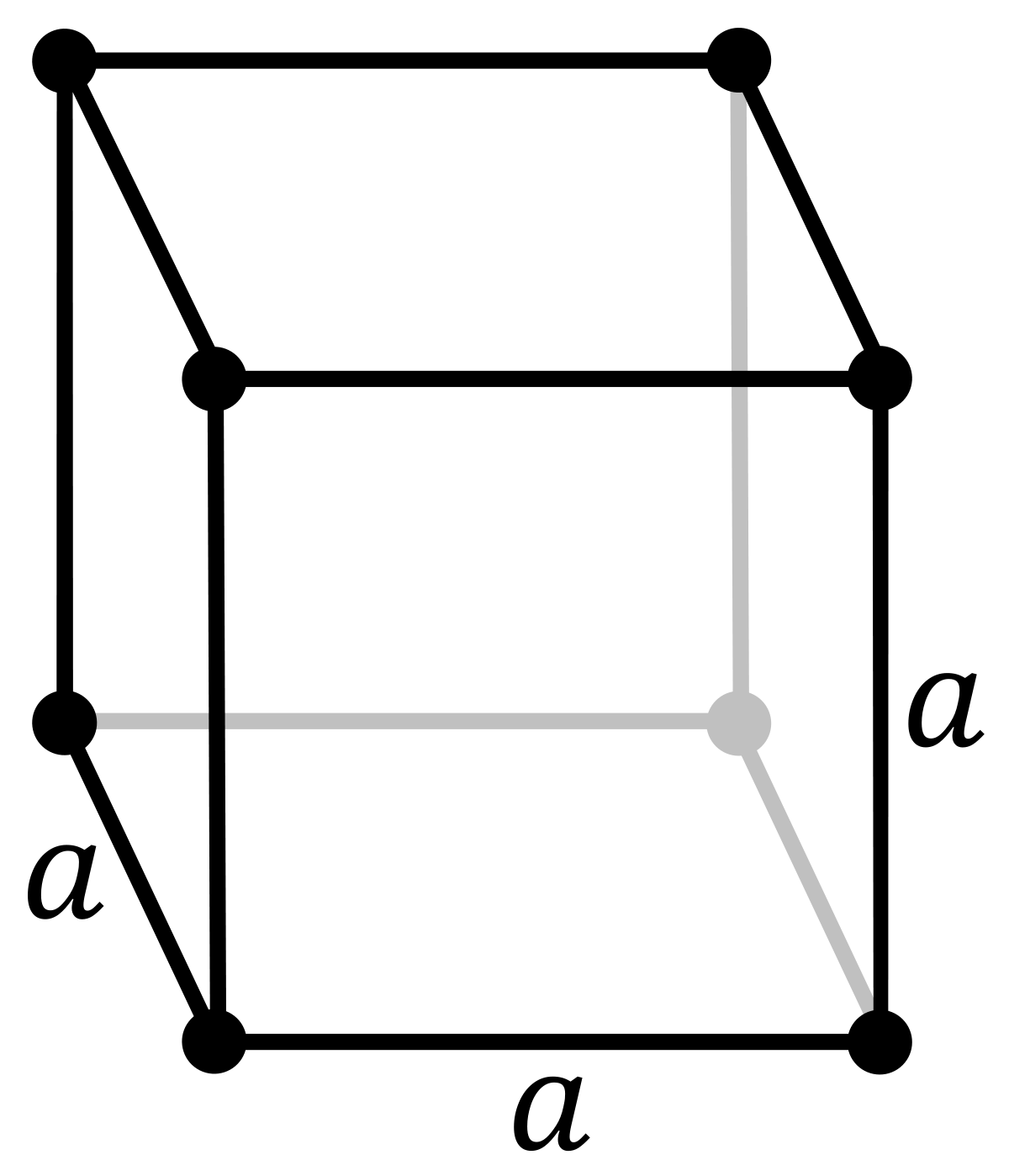
Le réseau peut être visualisé comme un système de balles liées par des ressorts. La figure ci-dessous illustre deux types de réseau décrits de cette manière. La figure de gauche montre un réseau cubique (réseau correspondant à un nombre important de solides cristallins, dont notamment de nombreux métaux). La figure de droite montre une chaîne linéaire, un réseau très simple permettant une approche aisée de la modélisation des phonons. Pour plus d'information sur les réseaux cristallins, voir l'article cristallographie.
L'énergie potentielle du réseau peut maintenant s'écrire :
- ω est la pulsation propre des potentiels harmoniques
- m est la masse des atomes.
- Ri est la coordonnée du ième atome, considéré maintenant par rapport à sa position d'équilibre.
- le symbole pv indique que la sommation est effectuée uniquement sur les plus proches voisins.
Ondes dans un réseau
Du fait des forces s'exerçant entre les différents atomes du réseau cristallin, le déplacement d'un ou plusieurs atomes autour de leur position d'équilibre entraînera une série d'ondes de vibrations se propageant dans le réseau. La figure ci-contre montre une onde de vibration dans un réseau. L'amplitude de l'onde est donnée par l'amplitude du déplacement des atomes autour de leur position d'équilibre. La longueur d'onde correspond au plus petit intervalle entre deux répétitions identiques de l'arrangement des atomes. Elle est notée λ sur la figure.
Toutes les longueurs d'onde de vibration ne sont pas possibles. Notamment, il existe une longueur d'onde minimale donnée par la distance entre les atomes a. Nous verrons plus loin qu'une onde de longueur d'onde plus faible que a est en fait identique à une longueur d'onde plus grande que a.
Toutes les vibrations possibles du réseau ne possèdent pas nécessairement une longueur d'onde (ou une fréquence) bien définie. C'est cependant le cas pour les modes normaux de vibration (les vibrations élémentaires du réseau), que nous allons examiner plus en détails dans les paragraphes suivants.
Phonons dans un réseau 1D
Considérons une chaîne unidimensionnelle composée de N atomes pour lesquels les potentiels sont harmoniques. Ce système est le modèle le plus simple pour un réseau cristallin. Le formalisme mathématique que nous allons développer dans la suite (dans le cadre de la mécanique quantique) est facilement généralisable à des systèmes à deux ou trois dimensions.
-
- m est la masse des atomes.
- Xi est l'opérateur position.
- Pi est l'opérateur impulsion
Une description plus approfondie de cet Hamiltonien est donnée dans l'article oscillateur harmonique quantique
- Définissons maintenant N "coordonnées normales" Qk définies comme les transformées de Fourier des opérateurs position Xi.
- Définissons également N "moments conjuguées" Πk définis comme les transformées de Fourier des opérateurs impulsion Pi.
La quantité k est le nombre d'onde du phonon, c’est-à-dire 2π divisé par la longueur d'onde. Ce nombre prend des valeurs quantifiées parce que le nombre d'atomes du système est fini. La forme de la quantification dépend du choix des conditions aux limites. Par souci de simplification, nous imposons dans la suite des conditions aux limites périodiques (aussi appelées conditions de Born von Karman), c’est-à-dire que nous considérons que l'atome N+1 est équivalent au premier atome. Physiquement, cela correspond à former une boucle avec la chaîne en faisant se rejoindre les deux extrémités. Le résultat de la quantification est :
La limite supérieure de n provient de la condition au limite choisie (l'atome en position x1 est identique à l'atome en position xN+1.
En inversant la transformée de Fourier pour exprimer les Qk en termes de Xi et les Πk en termes de Pi, et en utilisant les relations de commutations canoniques entre les Xi et les Pi, on peut montrer que (voir l'article mécanique quantique) :
En d'autres mots, les coordonnées normales Qk et leurs moments conjuguées Πk obéissent aux mêmes relations de commutation que les opérateurs position Xi et impulsion Pi. En fonction de ces grandeurs, le Hamiltonien s'écrit :
avec
Le couplage entre les variables positions a été transformé. Si les Qk et les Πk étaient hermitiens (ce qui n'est pas le cas), le Hamiltonien transformé décrirait N oscillateurs harmoniques non couplées. En fait, ce Hamiltonien décrit une théorie quantique des champs de bosons non interagissant.
Le spectre des énergies propres de ce Hamiltonien est obtenu en utilisant les opérateurs adjoints création et annihilation ak† et ak définis comme :
Pour plus de précisions, voir l'article Oscillateur harmonique quantique. Les opérateurs adjoints vérifient l'identité :
Comme dans le cas de l'oscillateur harmonique quantique, on peut montrer que les opérateurs ak† et ak correspondent respectivement à la création et l'annihilation d'une excitation d'énergie ℏωk. Cette excitation est un phonon.
On peut immédiatement en déduire deux propriétés importantes des phonons. D'abord, les phonons sont des bosons : n'importe quel nombre d'excitations identiques peuvent être créées par l'application répétée de l'opérateur création ak†. En second lieu, chaque phonon est un "mode collectif" correspondant au mouvement de la (quasi) totalité des atomes du réseau. Cette seconde conclusion se voit dans le fait que les opérateurs adjoints contiennent des sommations sur les positions et les impulsions de tous les atomes du réseau.
Il n'est pas évident a priori que les excitations générées par les opérateurs adjoints sont littéralement des ondes de déplacement d'atomes du réseau. On peut s'en convaincre en calculant la fonction de corrélation position-position. Soit |k> un état pour lequel un seul quantum de mode k est excité, c’est-à-dire :
On peut alors montrer que pour deux atomes i et j quelconques :
ce qui est exactement le résultat attendu pour une onde du réseau de pulsation ωk et de nombre d'onde k.
Phonons dans un réseau 3D
La généralisation à trois dimensions du modèle unidimensionnel précédent est aisée (mais assez lourde). Le nombre d'onde k est remplacé par un vecteur à trois dimensions, le vecteur d'onde
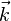
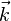
Le nouvel indice s=1, 2, 3 correspond à la polarisation des phonons. En effet, dans un modèle unidimensionnel, les atomes ne peuvent vibrer que sur une ligne, et tous les phonons correspondent à une onde longitudinale. En revanche en trois dimensions, la vibration ne se fait plus uniquement dans la direction de propagation, mais peut également lui être perpendiculaire. Elle correspond alors à une onde transverse. Cela donne naissance à des coordonnées normales supplémentaires, qui comme l'expression du Hamiltonien l'indique, correspondent à des espèces indépendantes de phonons.
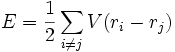
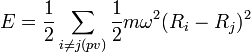
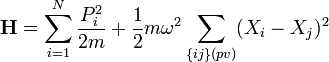
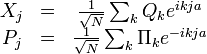
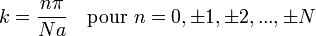
![\left[ Q_k , \Pi_{k'} \right] = i \hbar \delta_{k k'} \quad ;\quad \left[ Q_k , Q_{k'} \right] = \left[ \Pi_k , \Pi_{k'} \right] = 0](https://static.techno-science.net/illustration/Definitions/autres/c/cdecfe4f3b66be4df3495326ad4d62a2_a28a0b7bf0ebcfa401413420f7f21161.png)
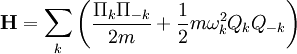
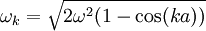
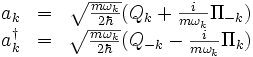
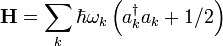
![[a_k , a_{k'}^{\dagger} ] = \delta_{kk'}](https://static.techno-science.net/illustration/Definitions/autres/c/c5052c89ba2167155b7bfe568f8f37d1_b67f7cf7a2a82fe8b6af079c6d16b3b9.png)
![[a_k , a_{k'} ] = [a_k^{\dagger} , a_{k'}^{\dagger} ] = 0.](https://static.techno-science.net/illustration/Definitions/autres/5/54686099e03a6e896a4ac9e9843ca83c_557bc74da6301aee2a016309cdbceb3a.png)
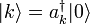
![\langle k | x_i(t) x_j(0) | k \rangle = \frac{\hbar}{Nm\omega_k} \cos \left[ k(i-j)a - \omega_k t \right] + \langle 0 | x_i(t) x_j(0) |0 \rangle](https://static.techno-science.net/illustration/Definitions/autres/3/3cd2d3ebe91859531adfa27ea0c80f72_d4f695e63854da9e79b8d2a6f89c63ba.png)