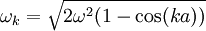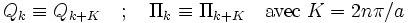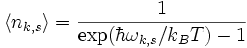Phonon - Définition

Introduction

Modes normaux de vibration progressifs de différentes fréquences ν dans un cristal. En mécanique classique, l'énergie emmagasinée dans chacun de ses modes peut varier continuement. En mécanique quantique, chacun de ces modes possède une énergie quantifiée E = (n+1/2) hν, où n est un entier indiquant le nombre de phonons ; les modes ne peuvent acquérir ou céder de l'énergie que par paquets de hν.

En physique de la matière condensée, un phonon (du grec ancien φονη / phonê, la voix) désigne un quantum d'énergie de vibration dans un solide cristallin : lorsqu'un mode de vibration du cristal de fréquence définie ν cède ou gagne de l'énergie, il ne peut le faire que par paquets d'énergie hν, h étant la constante de Planck. Ce paquet est considéré comme une quasi-particule, à savoir une particule fictive appelée phonon. Le cristal est alors réputé échanger des phonons lorsqu'il perd ou gagne de l'énergie. Le concept permet une analogie avec la lumière qui possède des propriétés similaires : elle se manifeste tantôt comme une onde, tantôt comme un paquet d'énergie hν, qui correspond à une particule élémentaire — non fictive cette fois — appelée photon.

Le phonon est une notion de mécanique quantique faisant appel au concept de dualité onde-corpuscule : selon le contexte expérimental il peut se manifester soit comme une onde, soit comme un paquet élémentaire. Si l'étude des phonons prend une part importante dans la physique de la matière condensée, c'est qu'ils jouent un rôle important dans un grand nombre de propriétés physiques des solides dont

• la capacité calorifique, ou capacité à échanger la chaleur ;
• la conductivité thermique, ou capacité à conduire la chaleur ;
• la conductivité électrique, ou capacité à conduire le courant électrique ;
• la capacité à propager le son.

La mécanique classique, qui ne prend en compte que l'accès vibratoire, n'est pas capable d'expliquer en totalité ces propriétés.

Introduction

Solide cristallin en mécanique classique

Les phonons sont l'équivalent en mécanique quantique d'une catégorie particulière de mouvement vibratoires connus sous le nom de modes normaux de vibration en mécanique classique. Un mode normal de vibration est un mode dans lequel chaque élément d'un réseau vibre à la même fréquence. Ces modes ont une grande importance, notamment parce que tout mouvement de type vibration dans un solide peut être représenté comme la superposition d'un certain nombre de modes normaux de vibration de fréquences différentes : ils peuvent être compris comme les vibrations élémentaires du réseau.

Quantification des modes de vibration

Bien que les modes normaux de vibration soient des entités de type ondulatoire, ils peuvent acquérir en partie un comportement de type particulaire quand le réseau est étudié au travers des lois de la mécanique quantique (du fait de la dualité onde-corpuscule). Ils sont alors nommés phonons. Les phonons sont des quasi-particules de spin 0 (bosons qui obéissent donc à la statistique de Bose-Einstein).

Comportement et propriétés des phonons

Courbe de dispersion

Dans la discussion des phonons dans un modèle unidimensionnel, nous avons obtenus une équation liant la pulsation d'un phonon ω_k à son nombre d'onde k :

Cette équation est connue sous le nom de relation de dispersion. La courbe ci-contre décrit son comportement.

La vitesse de propagation d'un phonon dans le réseau, qui correspond notamment à la vitesse de propagation du son dans un solide, est donnée par la pente de la relation de dispersion : ∂ω_k/∂k. Avec de faibles valeurs de k (c’est-à-dire aux grandes longueurs d'onde), la relation de dispersion est presque linéaire, et la vitesse du son est proche de ωa, indépendamment de la fréquence du phonon. En conséquence, un paquet de phonons de longueurs d'onde différentes (mais grandes) peut se propager sur de longues distances dans un réseau sans que les phonons se séparent. C'est la raison pour laquelle le son se propage dans les solides sans distorsion significative (en quelque sorte, les ondes de grande longueur d'onde ne sont pas influencées par la structure microscopique du matériau). Ce comportement n'est plus vrai pour de grandes valeurs de k (c’est-à-dire des longueurs d'onde courtes), pour lesquelles la vitesse de propagation dépend de manière significative de la longueur d'onde.

La physique du son dans les solides est très différente de la physique du son dans l'air, bien qu'il s'agisse dans les deux cas d'ondes de vibration. Ceci est dû au fait que dans l'air, le son se propage dans un gaz formé de molécules animées de mouvement aléatoires, et non pas dans un réseau organisé.

Phonons acoustiques et phonons optiques

Dans un solide réel, il y a deux types de phonons : des phonons "acoustiques" et "optiques". Les phonons acoustiques, qui sont ceux que nous avons décrits dans les parties précédentes, correspondent typiquement aux ondes sonores dans le réseau. Les phonons acoustiques de type longitudinaux et transverses sont souvent écrits de manières abrégée LA et TA respectivement.

Les phonons optiques sont présents dans les solides qui comportent plusieurs atomes par maille. Ils sont appelés "optiques" parce que dans les cristaux ioniques (comme par exemple le chlorure de sodium) ils sont très facilement excités par des ondes lumineuses (dans le domaine de l'infrarouge). Ceci est dû au fait qu'ils correspondent à des modes de vibration pour lesquels les ions positifs et négatifs situés sur des sites adjacents du réseau se rapprochent et s'éloignent les uns des autres en créant un moment dipolaire électrique oscillant avec le temps. Les phonons optiques qui interagissent de cette manière avec la lumière sont dits actifs dans l'infrarouge. Les phonons optiques qui sont actifs en spectrométrie Raman peuvent aussi interagir avec la lumière au travers de la diffusion Raman. Les phonons optiques de type longitudinaux et transverses sont souvent écrits de manières abrégée LO et TO respectivement.

Il est possible de trouver plus de renseignements sur les modes de vibration dans des articles traitant de la théorie de groupes.

Pseudo-moment

Il est tentant de considérer un phonon de vecteur d'onde comme s'il possédait un moment , par analogie avec les photons, ou toutes les ondes correspondant à un corpuscule (dualité onde-corpuscule). Ce n'est pas tout à fait correct, car n'est pas réellement un moment physique. Il est nommé pseudo-moment ou moment de vibration. Ceci est dû au fait que n'est déterminé qu'à un multiple de vecteur constant près, vecteur du réseau réciproque. Par exemple, dans un modèle unidimensionnel, les coordonnées normales Q et Π sont définies de telle manière que :

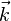
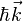
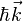
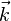
quel que soit le nombre entier n. Un phonon de nombre d'onde k est donc équivalent à un nombre infini d'autres phonons de la même famille de nombres d'onde k±2π/a, k±4π/a (etc). Les électrons de Bloch obéissent au même type de restrictions.

Généralement, on ne considère que les phonons de vecteurs d'onde de chaque famille possédant le plus "petit" vecteur . L'ensemble de ces vecteurs définit la première zone de Brillouin. D'autres zones de Brillouin peuvent être définies comme des copies de la première zone, décalées d'un multiple de vecteurs du réseau réciproque.

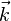
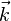
Propriétés thermodynamiques

Un réseau cristallin au zéro absolu est dans son état de base, et aucun mode de phonon n'est excité. D'après les lois de la thermodynamique, lorsqu'un réseau cristallin est à une température supérieure au zéro absolu, son énergie n'est pas constante mais elle fluctue de manière aléatoire autour d'une valeur moyenne. Ces fluctuations d'énergie sont dues à des vibrations aléatoire du réseau, qui peuvent être vues comme un gaz de phonons (le mouvement aléatoire des atomes du réseau correspond à la chaleur). Comme ces phonons sont liés à la température du réseau, ils sont parfois nommés « phonons thermiques ».

Contrairement aux molécules qui forment un gaz ordinaire, les phonons thermiques peuvent être créés ou annihilés par des fluctuations d'énergies aléatoires. Leur comportement est similaire au gaz de photons produit par une cavité électromagnétique, pour laquelle les photons peuvent être absorbés ou émis par les parois de la cavité. Cette similitude n'est pas une coïncidence : le champ électromagnétique se comporte en effet comme un groupe d'oscillateurs harmoniques (voir rayonnement du corps noir). Les deux gaz obéissent à la statistique de Bose-Einstein, c’est-à-dire qu'à l'équilibre thermique, le nombre moyen de phonons ou de photons dans un état donné est :

• ω_k,s est la pulsation du phonon ou du photon dans l'état
• k_B est la constante de Boltzmann
• T est la température (en Kelvin)

On peut remarquer que le potentiel chimique d'un gaz de photons ou de phonons est nul.

Ce type de considérations a mené au modèle de Debye décrivant le comportement de la capacité thermique des solides cristallins grâce aux phonons qu'ils contiennent. Ce modèle présente un meilleur accord avec les résultats expérimentaux que les précédents modèles : la loi de Dulong et Petit et le modèle d'Einstein.